基于随机响应面法的金鸡岭岩质边坡可靠度分析及抽样方法对比

doi:10.11872/j.issn.1005-2518.2018.03.297

基于随机响应面法的金鸡岭岩质边坡可靠度分析及抽样方法对比

盛建龙, 翟明洋^*

1武汉科技大学资源与环境工程学院，湖北武汉 430081

Reliability Analysis and Sampling Method Comparison of Jinjiling Rock Slope Based on Stochastic Response Surface Method

SHENG Jianlong, ZHAI Mingyang^*

1College of Resources and Environment Engineering，Wuhan University of Science and Technology，Wuhan 430081，Hubei，China

通讯作者: 翟明洋（1993-），男，湖北襄阳人，硕士研究生，从事岩土工程研究工作。807349283@qq.com

第一联系人: 盛建龙（1964-），男，湖南湘阴人，教授，从事岩土工程和采矿工程研究工作。wkdsjl@163.com

收稿日期: 2017-09-20 修回日期: 2018-01-26 网络出版日期: 2018-04-30

Received: 2017-09-20 Revised: 2018-01-26 Online: 2018-04-30

摘要

结合有限元滑面应力法和Hermite随机响应面法建立了金鸡岭岩质边坡稳定可靠度非侵入式分析模型，在此基础上研究了均匀设计抽样、LHS抽样、改进LHS抽样和分层抽样4种抽样配点方法对随机响应面的拟合精度、边坡失效概率及安全系数统计特征的影响。结果表明：（1）金鸡岭岩质边坡未支护状态下的失效概率约为18.4%，失稳风险较大，需采取支护加固措施；（2）改进LHS抽样和LHS抽样所构造的随机响应面具有较好的拟合精度，抽样配点效果优于分层抽样和均匀设计抽样；（3）建议边坡可靠度非侵入式随机分析采用改进LHS抽样或LHS抽样进行随机响应面的抽样配点计算，并尽可能多地选取样本点以外的验算点对随机响应面拟合精度进行校验。

关键词： Hermite随机响应面法 ; 滑面有限元应力法 ; 边坡可靠度分析 ; 抽样配点方法 ; Monte-Carlo法 ; LHS抽样 ; 失效概率 ; 拟合精度

Abstract

The non-invasive analysis model of Jinjiling rock slope stability is established based on the finite element sliding stress method and Hermite stochastic response surface method.The influence of four typical sampling methods like uniform sampling，LHS sampling，improved LHS sampling and stratified sampling on the random response surface’s fitting accuracy，slope failure probability and statistical characteristics of safety factor are studied.The results indicate that：（1）Jinjiling rock slope’s failure probability is about 18.4%，which is dangerous and needs proper support and reinforcement measures.（2）The random response surfaces constructed by LHS sampling and improved LHS sampling have better fitting accuracy，and the sampling allocation effect is better than that of stratified sampling and uniform design sampling.（3）It is suggested that the sampling allocation of random response surface should be calculated by improved LHS sampling or LHS sampling in the process of non-intrusive random analysis of slope reliability.

Keywords： Hermite stochastic response surface method ; finite element sliding stress method ; reliability analysis of slope stability ; sampling allocation method ; Monte-Carlo method ; LHS sampling ; failure probability ; fitting accuracy

PDF (2703KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

盛建龙, 翟明洋. 基于随机响应面法的金鸡岭岩质边坡可靠度分析及抽样方法对比. 黄金科学技术[J], 2018, 26(3): 297-304 doi:10.11872/j.issn.1005-2518.2018.03.297

SHENG Jianlong, ZHAI Mingyang. Reliability Analysis and Sampling Method Comparison of Jinjiling Rock Slope Based on Stochastic Response Surface Method. Gold Science and Technology[J], 2018, 26(3): 297-304 doi:10.11872/j.issn.1005-2518.2018.03.297

边坡工程作为一种复杂的岩土系统工程，其稳定性受到诸多因素的影响。这些因素往往具有不确定性，由于对边坡不确定性研究和认识不足导致的滑坡灾害时有发生。一般认为岩土工程不确定性因素主要分为两类：一类是物理不确定性因素，如力学参数空间变异性、应力场和渗流场分布、振动荷载及自然降雨影响等，这类不确定性因素是物理量本身的固有属性，无法完全消除但可以运用控制手段降低影响；另一类是认知不确定性因素，如分布参数的统计不确定性、各种力学模型及失效准则的模型不确定性、系统行为传播机理的传播不确定性等，这类不确定性因素需要发展新的研究理论、分析评价方法及监测防控技术予以降低^[1]。近年来，可靠度理论因同时考虑了岩土系统工程内部和外部不确定性因素的影响而在岩土工程中得到了广泛应用。边坡工程可靠度分析方法主要有2种：将确定性分析与随机分析进行耦合的随机有限元法^[2]和将二者独立展开进行的非侵入式分析方法^[3]。随机有限元方法将概率分布参数嵌入有限元数值分析过程中，编程复杂，计算量较大，因此难以在工程上推广。然而，在随机有限元法的基础上发展起来的非侵入式随机分析方法因解耦了确定性分析与随机分析过程，计算量显著减少、计算精度提高且分析方法更为灵活，因此得到了工程界的广泛关注。

1998年，美国学者Isulapalli等^[4]首次提出了随机响应面法并率先将其应用于环境和生物系统不确定性分析。近年来，许多学者开展了边坡工程非侵入式随机分析方法的研究，如：蒋水华等^[5]首次将非侵入式随机分析方法运用于水电工程复杂三维开挖边坡的可靠度计算；李典庆等^[6]将此法运用于洞室变形可靠度计算及敏感性分析；胡冉等^[7]采用此法研究了心墙堆石坝渗透可靠度问题。上述研究主要针对可靠度分析方法和参数变异性等方面，却忽略了非侵入式随机分析的关键问题，即随机抽样配点方法对可靠度分析的影响。随机抽样配点方法决定了样本观测点在变量分布空间的位置，对响应面函数的拟合精度、可靠度分析结果和安全系数统计特征等有着重要影响。因此，本文在采用Hermite随机响应面法对岩质边坡进行可靠度分析的基础上，系统对比分析了常见的4种抽样配点方法对响应面拟合精度和可靠度分析结果的影响，为岩土工程可靠度分析时抽样方法的选取提供参考。

1 基本理论

1.1

1.1 有限元滑面应力法

有限元滑面应力法（Slip Surface Stress Method，简称SSSM）是一种基于有限元算法的边坡稳定性数值分析方法^[8]。在求解边坡初始应力场的基础上，通过对滑面S上的真实抗剪力和滑动抗剪力进行积分，将安全系数定义为二者的比值，可表示为

$F_{S} = \frac{\int_{A}^{B} τ_{f} d S}{\int_{A}^{B} τ d S} = \frac{\overset{n_{s}}{\sum_{i = 1}} τ_{f_{i}} l_{i}}{\overset{n_{s}}{\sum_{i = 1}} τ_{i} l_{i}}$

（1）

式中： $F_{S}$ 为安全系数； $τ_{f}$ 为真实抗剪强度； $τ$ 为真实剪应力； $n_{s}$ 为滑面底部土条数目； $l_{i}$ 为第 $i$ 个土条底沿滑面长度； $τ_{f_{i}}$ 、 $τ_{i}$ 分别为第 $i$ 个土条底部真实抗剪强度和抗剪力。

相比极限平衡法，该方法考虑了岩土材料应力应变本构模关系和初始应力场对边坡稳定性的影响。而较之有限元强度折减法，该方法具有计算量小、易获取潜在滑面位置和运行速度快等优点。有限元滑面应力法可借助GEOSTUDIO等岩土仿真软件实现。具体做法：首先采用SIGMA/W程序进行有限元原位计算，求解边坡初始应力场分布，将每个积分点的应力映射到单元节点并取节点应力平均值，然后将计算结果导入SLOPE/W模块进行边坡稳定性分析，通过沿滑面底部划分土条，根据土条底部中点应力、滑面倾角和土条长度等信息计算每个土条底部的真实抗剪强度和剪应力，最后通过该模块自带的剪入剪出方法或其他自动搜索法搜索临界滑面和临界安全系数 $F_{S m i n}$ 。

1.2

1.2 Hermite随机响应面法

由于边坡工程的复杂性和岩土结构的不确定性，边坡输出响应量（安全系数、位移和孔隙水压力等）往往为输入变量（ $c$ 、 $φ$ 等）的高度非线性隐式函数。边坡可靠度分析一般采用多项式响应面（RSM）插值技术^[9]寻找合理的插值多项式（即响应面函数）近似代替边坡的真实功能函数。拟采用Hermite随机响应面法（SRSM）构建边坡响应面，该方法自1998年被提出后得到了广泛应用和发展^{[10,11,12,13]}。根据文献[4]可知，随着Hermite随机多项式阶次的增高，多项式展开待定系数数目显著增加。为保证计算精度并减少计算量，拟采用二阶Hermite随机多项式展开建立边坡输出响应量与输入函数之间的近似显式表达

$F (X) = a_{0} + \overset{N}{\sum_{i = 1}} a_{i} X_{i} + \overset{N}{\sum_{i = 1}} a_{i, i} (X_{i}^{2} - 1) + \overset{N - 1}{\sum_{i = 1}} \overset{N}{\sum_{j > 1}} a_{i, j} X_{i} X_{j}$

（2）

则边坡功能函数可表示为

$G (X) = F (X) - 1.0$

（3）

待定系数数目可表示为

$N_{c} = \frac{(N + p)!}{N! p!}$

（4）

式中： $X = (X_{1}, X_{2}, \dots, X_{N})^{T}$ 为独立标准正态随机向量，对应相应的随机变量； $N$ 为随机变量数目； $a = (a_{0}, a_{i}, \dots a_{i, j})$ 为待定系数， $N_{c}$ 为待定系数数目， $p$ 为随机多项式阶次。

1.3

1.3 抽样配点方法

常用的概率抽样配点方法有均匀设计抽样、拉丁超立方抽样（LHS）、改进拉丁超立方抽样和分层抽样等。以上述4种抽样方法作为研究对象，根据各抽样方法原理要求，借助EXCEL电子表格及MATLAB的randperm（）函数将产生的初始样本数列随机打乱，最终产生N组抽样样本点。

均匀设计抽样是在均匀选取设计水平的基础上，利用均匀设计表及其使用表来设计试验方案，使试验点均匀散布于样本空间^[14]。采用MATLAB编制均匀设计表 $U_{n}^{*} (q^{s})$ 辅助设计抽样试验方案，其中 $n$ 为试验次数， $q$ 为各因素水平数， $s$ 为因素个数。LHS是利用均匀分布 $U (0,1)$ 和逆变换法将样本空间均分进而随机扰动产生的随机数，生成 $N$ 维随机向量，该方法能够使样本点均匀分层分布于整个随机变量样本空间，因而得到广泛应用。为了降低LHS抽样随机性，提高抽样精度和计算效率，许多学者对LHS进行了改进并产生了不错的抽样效果^{[15,16,17,18]}。拟采用文献[12]所提出的改进LHS方法，该方法采用双层样本点选取原则，第一层为系统响应整体模拟，在抽样空间 $[- 3 σ, 3 σ]$ 或整个样本空间中抽取少量样本并选取最优点存在的最大概率区域（一般认为在均值附近），第二层在最优点附近的某个小邻域内（如 $[- σ, σ]$ ）随机选取较多的点，该方法可通过少量样本模拟得到尽可能精确的系统响应。分层抽样是以 $\pm m σ$ （ $m$ 可取 $\pm 1$ ， $\pm 1.5$ ， $\pm 2$ ）为界限，将样本空间划分为若干互不交叉的层，在每一层进行随机抽样，根据每层的概率分布确定该层抽样数目，总抽样数目等于试验次数。图1为各抽样方法二维样本点分布图。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 各抽样配点方法二维样本点分布

由样本点分布可知，均匀设计抽样减小了样本点的随机性，样本点分布呈现规律性，均匀分布于样本空间；而LHS抽样和改进LHS抽样的样本点主要集中于变量均值附近，改进LHS抽样产生的样本点较LHS抽样样本点更为集中；分层抽样样本点分布区域较广，样本点覆盖到了变量概率分布的尾部。

2 边坡可靠度非侵入式分析模型

2.1

2.1 边坡工程概况

金鸡岭岩质边坡最大坡高33.4m，分为三级，第一级边坡坡率约为1∶0.8，坡高8 m，宽度约为2 m；第二级边坡坡率约为1∶0.9，坡高9 m，宽度为1.5~2.0 m；第三级边坡坡率为约为1∶1.0，最大坡高为13 m。边坡地质条件单一，边坡由矽卡岩强风化岩体及其接触变质带构成，接触变质带节理裂隙发育，规律较差。岩体内发育2组节理剪节理，节理面平直光滑，基本不张开，无充填，延展性差，长度一般为3～5 m。上部覆盖0.5~2.5 m第四系残坡积层，局部地段有粉质粘土。边坡地表排水较好，勘察期间未见地下水。为简化计算不考虑结构面的影响，边坡简化几何模型如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 边坡简化几何模型

2.2

2.2 边坡有限元稳定性分析

不考虑边坡节理裂隙和降雨等因素的影响，选取岩质边坡7-7剖面进行有限元数值模拟分析。边坡上覆一层厚度为0.5~2.5 m的粉质粘土，下部为矽卡岩强风化层。由式（4）可知，Hermite随机多项式展开系数数目会随着随机变量数目的增大而增大，为减小计算量，将边坡稳定性影响程度较大的岩土参数 $c$ 、 $φ$ 和 $γ$ 作为随机变量，将 $E$ 和 $ν$ 视为常量。值得注意的是，岩土体力学参数并非总是服从独立正态分布，而是更偏向于服从其他分布类型（如对数正态分布）且参数之间具有相关性。对于相关非高斯分布随机变量，可借助Nataf变换将原始空间相关非正态随机变量表示为独立标准正态随机变量^[6]。假设所有随机变量均服从正态分布，且相互独立，随机变量变异系数COV参考Phoon等^[19,20]选取。岩土物理力学参数及统计特征见表1。采用GEOSTUDIO软件的SIGMA/W模块建立边坡有限元分析模型，见图3。

表1 岩土物理力学参数及统计特征

Table 1Physical and mechanical parameters and

力学参数	统计参数	粉质粘土	矽卡岩强风化岩层	分布类型
粘聚力c/kPa	均值μ	25.0	60.0	正态分布
粘聚力c/kPa	变异系数COV	0.25	0.22	正态分布
内摩擦角φ/（°）	均值μ	23.0	25.0	正态分布
内摩擦角φ/（°）	变异系数COV	0.16	0.15	正态分布
重度γ/（kN/·m^-3）	均值μ	18.8	21.5	正态分布
	变异系数COV	0.20	0.18	正态分布
弹性模量E/MPa		30.5	33 600.00	常量
泊松比（ν）		0.35	0.26	常量

新窗口打开| 下载CSV

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 边坡有限元分析模型

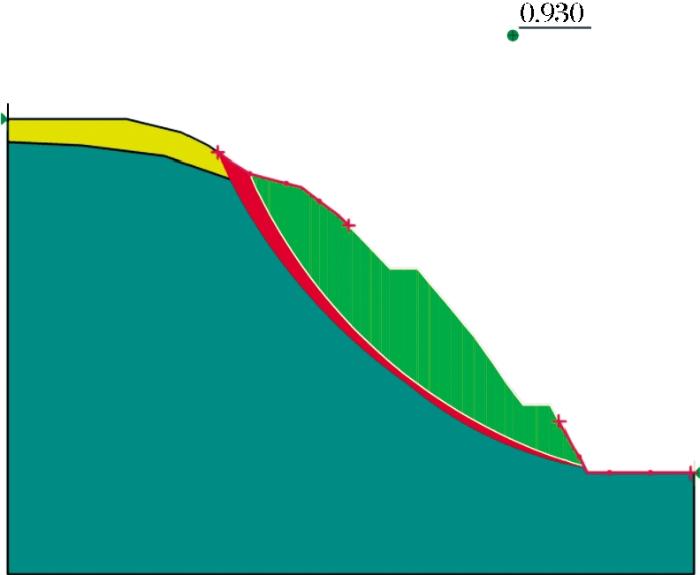
岩土材料为服从Mohr-Coulomb准则的弹塑性本构模型；模型左右边界施加水平位移约束，下边界为全约束；将模型划分为四边形和三角形网格，有限单元网格共4 152个，节点4 171个，对边坡表层存在滑坡危险的区域有限单元网格进行适当加密处理。将岩土力学参数均值输入有限元模型，计算所得的边坡安全系数为0.930，说明从确定性分析角度来看，该边坡稳定性很差，需立即采取加固措施。

2.3

2.3 边坡稳定可靠度分析模型

边坡可靠度分析过程中取随机变量 $X = (c_{1}, φ_{1}, γ_{1}, c_{2}, φ_{2}, γ_{2})$ ，随机变量数目 $N = 6$ 。由式（4）可知，二阶Hermite随机多项式展开系数 $N_{c} = 28$ ，因此每种抽样配点方法产生的配点数目 $N_{p}$ 应不小于 $N_{c}$ 。将上述4种抽样配点方法所得样本点输入边坡有限元滑面应力法分析模型，求解各试验方案对应的边坡安全系数。

本文涉及边坡稳定性分析次数较多，为避免重复多次进行有限元软件界面操作，可借助GEOSTUDIO生成的边坡稳定性分析计算源文件*.xml实现边坡稳定性快速分析^[18]。具体做法为采用文本编辑器打开并修改*.xml文件中对应的岩土材料赋值即可产生新的计算源文件。在获取边坡随机输入参数与输出响应量的基础上，采用最小二乘回归分析求解随机多项式展开系数得到响应面函数；然后对响应面函数的拟合度进行校验以确保响应面的精度；最后对经过校验的响应面函数采用10⁶次直接蒙特卡罗模拟（MCS）求解边坡失效概率并获取失效样本，进而对比分析边坡安全系数统计特征。图4给出了边坡可靠度分析计算流程图。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 边坡可靠度分析流程图

采用随机响应面法对边坡进行可靠度分析，鸡岭岩质边坡未支护状态下的失效概率约为18.4%；根据表2给出的失效概率与岩土结构安全性能的对应关系^[15]可知，该边坡失稳风险较大，需立即采取支护加固措施，该结果与确定性分析结果一致。可见，同时对边坡进行确定性分析和随机分析，有利于全面把握和评价工程安全性，为后续设计施工和支护加固提供更完备的科学依据。

表2 失效概率与岩土结构安全性能的关系

Table 2Relationship between failure probability and safety performance of geotechnical structure

失效概率	可靠度指标	性能水平	处理措施
3.0×10^-7	5	高	正常维护
3.0×10^-5	4	较好	正常交通情况下维护
0.001	3	平均安全水平以上	关闭以修复
0.006	2.5	平均安全水平以下	频繁停用以修复
0.023	2	较差	频繁较长时间停用以修复
0.07	1.5	不容乐观	集中修复
0.16	1	灾难性的	紧急行动以减轻灾害

新窗口打开| 下载CSV

3 抽样配点方法研究

3.1

3.1 响应面精度验算结果对比分析

在边坡可靠度分析之前须对响应面函数拟合精度进行验算，以确保分析结果的准确性。采用相关指数 $R^{2}$ 描述非线性回归响应面函数在整个空间上对真实功能函数的拟合精度。相关指数 $R^{2} \in (0,1)$ ， $R^{2}$ 越接近于1表示响应面函数拟合精度越高。计算公式为

$R^{2} = 1 - \frac{\overset{n}{\sum_{i = 1}} (y_{i} - y_{i}^{*})^{2}}{\overset{n}{\sum_{i = 1}} (y_{i} - {\bar{y}}_{i})^{2}}$

（5）

式中： $n$ 为实测样本点数目， $y_{i}$ 、 $y_{i}^{*}$ 分别为第 $i$ 个样本点对应的实测响应值和预测响应值， ${\bar{y}}_{i}$ 为第 $i$ 个样本点的实测响应均值。

响应面拟合精度与响应面函数形式及概率抽样配点方法有关。为研究抽样配点方法对响应面在整个变量定义域空间拟合精度的影响，不仅要验算响应面函数在样本点处的拟合精度，还需随机抽取若干个（取 $n' = 20$ ）抽样样本点之外的数据点进行验算，此时相关指数 $R^{2}$ 则反映响应面函数在整个空间上对真实功能函数的拟合精度。

将4种抽样配点方法产生的样本点实测响应值及Hermite随机多项式计算所得的预测响应值代入式（5）计算得到相关指数 $R^{2} \geq 0.9996$ ，说明该响应面函数在样本点处的拟合精度较高，可满足要求（表2）。随机抽取 $n'$ 个（取 $n' = 20$ ）抽样样本点之外的其他验算点进行 $R^{2}$ 验算。表3给出了各抽样配点方法对应的验算结果。

表3 各抽样配点方法对应的R²验算结果

Table 3Calculation results <i>R</i><sup>2</sup> corresponding to each sampling collocation method

计算点	均匀设计抽样	LHS	改进LHS	分层抽样
样本点	1	0.9996	0.9999	0.9999
其他验算点	0.9877	0.9972	0.998	0.991

新窗口打开| 下载CSV

由表3可见，根据4种抽样配点方法建立的Hermite随机响应面在样本点处的拟合精度均很高，但在样本点之外随机选取的其他验算点处拟合精度却存在明显差异。由均匀设计抽样构造的响应面虽在样本点处的 $R^{2} = 1$ ，拟合精度最高，但在样本点之外验算点处的拟合精度低于其他抽样方法。通过对比发现，改进LHS构造的响应面精度在样本点和样本点之外的验算点处拟合精度均较高。总体来说，改进LHS和LHS的抽样精度优于分层抽样和均匀设计抽样。不同抽样方法导致响应面拟合精度产生差异的原因在于均匀设计抽样基于均匀设计试验弱化了样本的随机性，减少了最优区域内的样本数量，且使部分样本点线性相关，这些因素制约了系统响应的拟合精度。分层抽样分层界限选取存在主观性且各维度样本水平可能会因随机打乱而偏离最优区域，从而影响响应面精度。LHS样本点兼具“分层”和“均匀”的分布特点，且保证了样本点覆盖到概率分布的两端，而改进LHS不仅具有LHS的优点且保证了最优点小邻域内的抽样数量，能够得到更加精确的系统响应，因此使响应面具备更优的拟合效果。上述分析表明，无论选用何种抽样配点方法，对边坡进行非侵入式可靠度分析时都有必要在整个参数空间对响应面的拟合精度进行验证，尤其需要选取样本点之外的验算点进行验证。若响应面精度不符合要求，应返回上一步对响应面函数形式及多项式展开系数进行调整和再验算。

3.2

3.2 边坡可靠度分析结果对比

为进一步揭示抽样配点方法对可靠度分析的影响，对比4种抽样配点方法对应的边坡失效概率统计特征，并将结果与Monte-Carlo法可靠度分析结果进行对比分析。表4给出了各抽样配点方法所得边坡失效概率均值 $P_{f}$ 及其变异系数 $C O V_{P_{f}}$ 。

表4 各抽样配点方法所得失效概率及其变异系数

Table 4Failure probability and its variation coefficient of different sampling collocation methods

抽样方法	$P_{f}$	$C O V_{P_{f}}$
Monte-Carlo法	0.1843	-
均匀设计抽样	0.2461	2.387×10^-7
LHS	0.1840	1.174×10^-7
改进LHS	0.1841	1.652×10^-7
分层抽样	0.2127	1.985×10^-7

新窗口打开| 下载CSV

由表4可见，基于改进LHS抽样的随机响应面法对边坡失效概率的计算精度最高，LHS次之；分层抽样和均匀设计抽样计算所得边坡失效概率均值相比改进LHS和LHS误差明显较大。因此4种抽样配点方法中，改进LHS和LHS适用于随机响应面的概率配点，而分层抽样和均匀设计抽样所得响应面对整个参数空间的拟合精度低于改进LHS和LHS，配点效果不佳。

图5给出了边坡功能函数的累积分布函数（CDF）曲线。从图5可见，改进LHS与LHS抽样所得功能函数的CDF曲线几乎重合，分层抽样和均匀设计抽样的CDF曲线与改进LHS及LHS存在明显差异，这充分说明对于随机响应面分析过程改进LHS和LHS的抽样配点效果优于分层抽样和均匀设计抽样。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 边坡功能函数的CDF曲线

4 结论

（1）结合有限元滑面应力法和Hermite随机响应面法，采用非侵入式随机分析方法对金鸡岭岩质边坡进行了可靠度分析。金鸡岭岩质边坡未支护状态下的失效概率约为18.4%，偏危险，需采取支护加固措施。

（2）对常见的4种抽样配点方法对响应面拟合精度和可靠度分析结果的影响进行了系统的对比分析。改进LHS和LHS均能够很好地保证所构造响应面的拟合精度、边坡失效概率及安全系数统计特征的准确性，由分层抽样和均匀设计抽样配点所得响应面对整个参数空间的拟合精度相对较低，可能使可靠度分析结果出现较大误差。在对实际工程的可靠度分析中，建议采用改进LHS和LHS抽样进行随机响应面的概率配点计算。另外边坡可靠度分析响应面法需在整个参数空间尤其是样本点以外的验算点对响应面拟合精度进行校验；若响应面精度不符合要求，应返回上一步对响应面函数形式及多项式展开系数进行调整和再验算。

SHENG Jianlong,ZHAI Mingyang.Reliability Analysis and Sampling Method Comparison of Jinjiling Rock Slope Based on Stochastic Response Surface Method[J].Gold Science and Technology,2018,26(3):297-304.盛建龙,翟明洋.基于随机响应面法的金鸡岭岩质边坡可靠度分析及抽样方法对比[J].黄金科学技术,2018,26(3):297-304.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

蒋水华.

水电工程边坡可靠度非侵入式随机分析方法

[D].武汉：武汉大学，2014.