为扩大生产能力和提高生产效率,矿山采取的方法主要是扩大采场的结构尺寸参数,即采场暴露面积[1,2,3,4]。通常情况下,当采场暴露面积过小时,采场生产效率低,矿石损失量大,矿山经济效益降低;而暴露面积过大,会增加大规模地压活动的概率,降低采场稳定性[5,6,7,8]。因此,若要提高矿山的生产效率必须在保障安全生产的前提下,尽可能地扩大采场结构尺寸,即优化采场暴露面积,计算采场极限暴露面积。目前,采场极限暴露面积的确定主要采用经验类比法和Mathews稳定图法[9,10,11]。这2种方法确定的参数范围大,人为影响程度高,难以从矿山开采的力学行为和工程响应来确定极限暴露面积[12,13]。此外,数值模拟分析方法常用于采场结构参数和开采顺序的优化[14,15,16],可获得合适的采场暴露面积,但受到计算模型的限制,难以高效确定采场极限暴露面积。
利用数值模拟采场暴露面积下的拉应力和压应力分布规律,建立暴露面积与最大拉应力、最大压应力的回归模型,可以有效减少计算工作量,高效确定采场极限暴露面积。采场暴露面积优化模型以采场顶板最大拉应力和两帮最大压应力与采场暴露面积之间的关系为基础,基于矿山岩体力学参数限值,在确定的合理安全值条件下,可用于回归优化采场极限暴露面积。
1 矿山概况
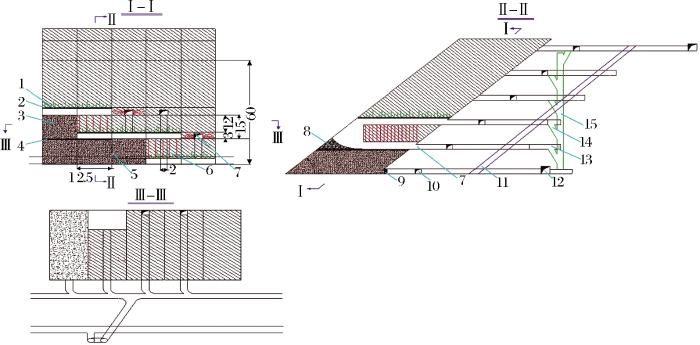
卧虎山矿床赋存于雁翎关组顶部含铁片岩中,由多个带状矿层组成,带状矿层呈NW-SE向展布,总体走向330°,倾向SW,倾角23°~68°,平均倾角为48°,长1 400 m,厚度一般为21~50 m,平均厚度为32 m,属于典型的倾斜中厚矿体。采用上向高分层预控顶嗣后充填采矿法(图1)。矿房垂直矿体走向布置,采场阶段高度为60 m,分4个分段回采,高度为15 m,矿房跨度为12.5 m,长度为矿体厚度。在每个矿房顶板进行锚杆支护,即预控顶,预控顶高度为3 m。每100 m设置间柱,间柱宽度为12 m,矿房不留顶底柱。矿房采用“隔一采一”的方式,矿房回采结束后采用上向高分层预控顶嗣后充填采矿法回采间柱。落矿采用CS-100D高风压潜孔钻机施工下向平行孔,采场出矿采用1 m³电铲和2 m³油铲,矿房回采完成后即进行充填。
图1
图1
上向高分层预控顶嗣后充填采矿法
1-锚杆;2-人工假顶;3-胶结充填体;4-分层底板;5-炮孔;6-切割天井;7-穿脉;8-矿石;9-充填挡墙;10-分层联络道;11-阶段斜坡道;12-阶段运输巷道;13-出矿巷道;14-分层溜井;15-阶段溜井
Fig.1
Pre-control top-to-high stratified filling mining method
2 采场极限暴露面积计算方案
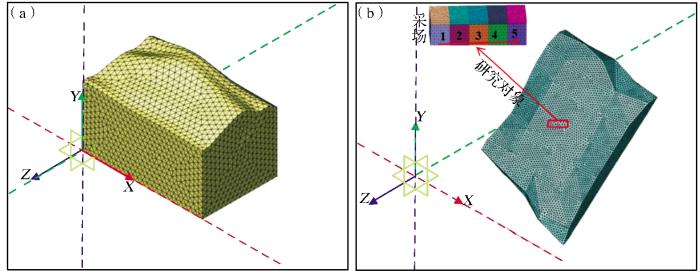
2.1 计算模型
图2
表1 卧虎山矿岩岩体力学参数
Table 1
| 岩体名称 | 弹性模量(E)/GPa | 泊松比( | 抗拉强度/MPa | 抗压强度/MPa | 内聚力( | 内聚力( | 密度( |
|---|---|---|---|---|---|---|---|
| 矿体 | 11.67 | 0.25 | 3.5 | 23.30 | 4.32 | 29.42 | 3 490 |
| 围岩 | 11.67 | 0.26 | 1.5 | 10.54 | 3.20 | 27.48 | 2 680 |
| 夹石 | 4.22 | 0.26 | 0.5 | 1.03 | 0.32 | 25.56 | 2 680 |
2.2 计算方案
在对采场结构参数进行优化之前,需掌握该地质条件下采场顶的板极限暴露面积,以指导采场参数的确定。由于在地质、水文等开采条件相同的情况下,采场暴露面积主要受采场长度和宽度的影响,因此分别对采场沿倾向长度(即采场 长度)为30 m和40 m 2种情况进行模拟,计算采场沿走向长(即采场跨度)分别为10.0,12.5,15.0,17.5,20.0 m时的采场极限暴露面积,模拟方案见表2。由表可知,10种模拟方案的采场暴露面积在300~800 m2之间。
表2 回采方案设计
Table 2
| 方案编号 | 因素 | ||
|---|---|---|---|
| 采场长度/m | 采场跨度/m | 采场暴露面积/m2 | |
| 1 | 30 | 10 | 300 |
| 2 | 30 | 12.5 | 375 |
| 3 | 30 | 15 | 450 |
| 4 | 30 | 17.5 | 525 |
| 5 | 30 | 20 | 600 |
| 6 | 40 | 10 | 400 |
| 7 | 40 | 12.5 | 500 |
| 8 | 40 | 15 | 600 |
| 9 | 40 | 17.5 | 700 |
| 10 | 40 | 20 | 800 |
3 模拟结果分析
3.1 计算结果
该矿山矿体赋存于浅部,模型顶部最大标高为312 m,上部分距离取平均值。将自重应力平衡后作为采场初始应力场,计算底部最大应力为8.6 MPa,上覆岩层的自重应力为8.67 MPa,模型底部和自重应力相互验证模拟结果的可信度。
图3
图3
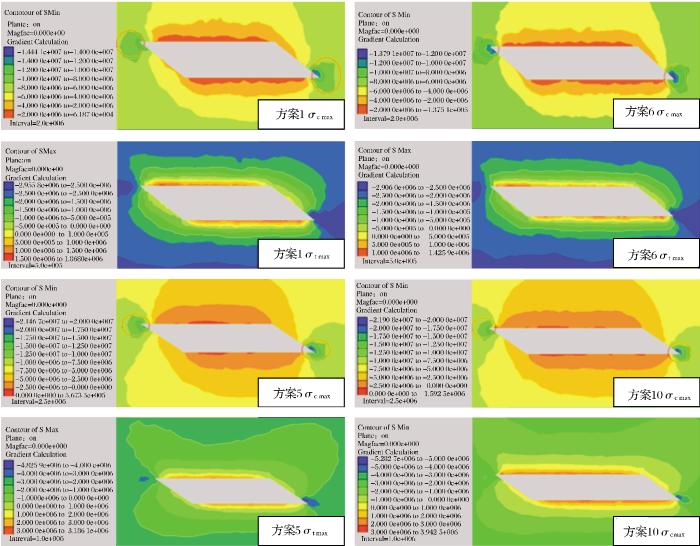
4种方案沿倾向主应力云图
Fig.3
Principal stress cloud along inclination of four schemes
表3 10种方案沿倾向应力值
Table 3
| 方案编号 | 顶板最大拉应力/MPa | 两帮最大压应力/MPa |
|---|---|---|
| 1 | 1.87 | 14.44 |
| 2 | 2.41 | 15.96 |
| 3 | 2.60 | 17.51 |
| 4 | 2.82 | 19.02 |
| 5 | 3.19 | 21.47 |
| 6 | 1.43 | 13.79 |
| 7 | 2.19 | 15.06 |
| 8 | 2.70 | 17.35 |
| 9 | 3.14 | 20.11 |
| 10 | 3.94 | 21.91 |
3.2 结果分析
由图3和表3可知,矿体开挖后,矿体上盘与采场底板交点处,以及采场下盘与采场顶板交点处(图3红圈内)均出现压应力集中现象,采空区顶板和底板均出现拉应力集中现象,且采空区下部围岩中的压应力明显大于上部,这是由于采空区形成后,上覆岩层的自重应力转移到采空区周边围岩内,加之围岩的埋深较大,所以压应力主要集中在上盘下部。顶底板拉应力均匀分布在顶底板上,且呈现出由采空区附近向四周均匀减小的趋势,这是由于采场垂直于矿体走向布置,顶底板面轴线位置平齐。顶板拉应力区域分布比下盘多且拉应力更大,这是由于上部顶板的自重应力转移到底板的围岩中,一方面顶板围岩受到重力和弹塑性变形的影响将会引起较大的位移,从而造成拉应力较大,另一方面底板围岩受到水平方向的挤压作用和自重应力的影响,开挖后向上位移的趋势减缓从而造成拉应力较小。因此,采空区顶板的拉应力区域和拉应力值更大。
研究结果表明,当矿房沿倾向方向长度一定时,周边围岩的应力绝对值随跨度增加基本呈增大的趋势。方案5、方案9和方案10中围岩中最大拉应力值分别达到3.19,3.14,3.94 MPa,超过了围岩的抗拉强度值,很有可能发生拉伸破坏,对岩体稳定性构成潜在威胁,说明方案5、方案9和方案10在实际生产中不可行。
4 采场极限暴露面积模型
4.1 回归模型的构建
图4
图4
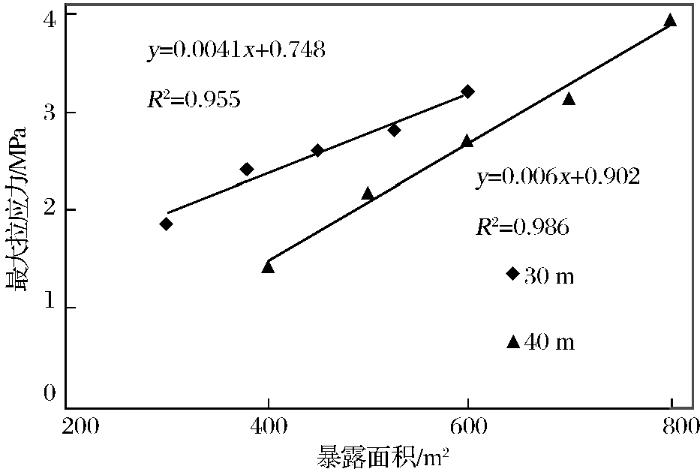
不同采场暴露面积条件下顶板最大拉应力
Fig.4
Maximum tensile stress of roof under different exposure area of stope
图5
图5
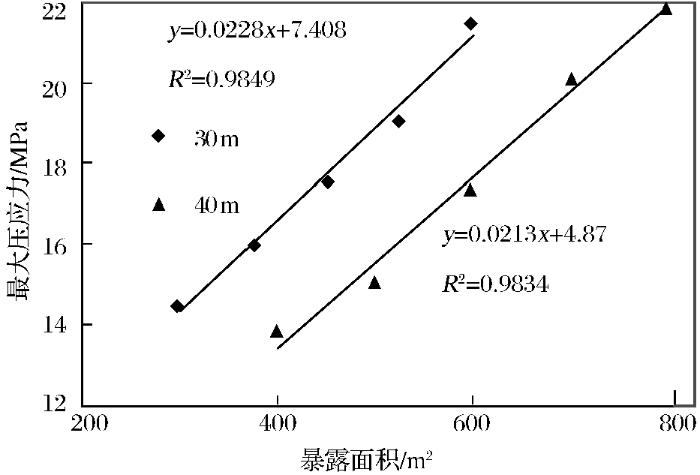
不同暴露面积条件下两帮最大压应力
Fig.5
Maximum compressive stress of wall rock under different exposure area of stope
表4 暴露面积与最大拉应力、最大压应力线性拟合结果
Table 4
| 应力类型 | 采场长/m | 斜率 | 截距 | 方差 | 规律模型 |
|---|---|---|---|---|---|
| 顶板最大拉应力 | 30 | 0.00407 | 0.748 | 0.955 | |
| 40 | 0.00597 | -0.902 | 0.986 | ||
| 两帮最大压应力 | 30 | 0.02283 | 7.708 | 0.9849 | |
| 40 | 0.02129 | 4.87 | 0.9834 |
4.2 采场暴露面积优化
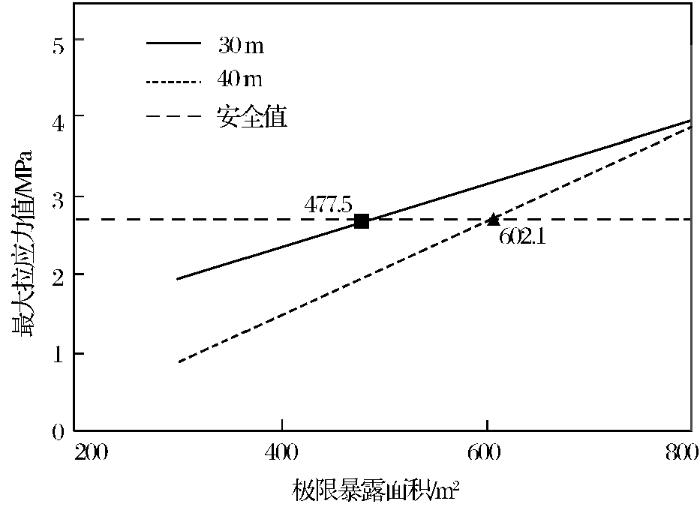
基于顶板最大拉应力和两帮最大压应力随采场暴露面积的变化规律,在已知采场应力限值的情况下,可以通过反演计算来优化采场暴露面积,即计算采场极限暴露面积。依据表1可知,矿体的抗拉强度和抗压强度分别为3.5 MPa和23.3 MPa。由于采矿出矿等生产作业在采场内进行,为了保证作业的生产安全,预留1.3的安全系数,计算出矿体拉应力和压应力限值分别为2.69 MPa和17.92 MPa。
图6
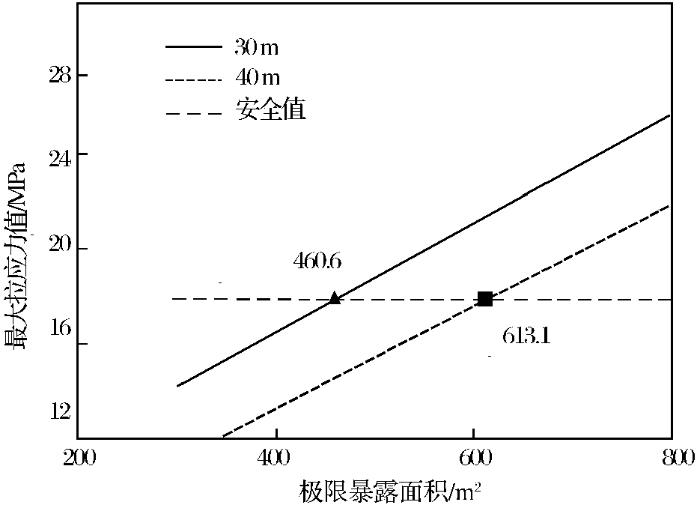
图7
在相同的拉压应力限值条件下,采场长40 m的极限暴露面积大于采场长30 m的极限暴露面积,这与采场形状系数有关,因此在合理的跨度值下,采场设计时应在许可范围内采取最大采场长度。当采场岩体力学参数发生改变时,可采用表3中的模型反演计算来确定采场极限暴露面积。
5 结论
(1)由采场稳定性分析可知,压应力出现在上盘下部,拉应力出现在顶底板且分布均匀。10种方案中方案5、方案9和方案10的拉压应力超过岩体抗拉压强度,不满足安全要求,其余几种方案符合最大强度理论要求。
(2)当采场暴露面积和跨度均相同且跨度小于15 m时,增加采场长度会改善采场应力情况。
(3)通过数值模拟计算得出10种方案下采场顶底板最大拉应力和最大压应力,通过线性拟合方法建立了采场暴露面积与最大拉应力和最大压应力的回归函数关系曲线。当矿山岩体力学参数发生改变时,可采用表4中的反演计算模型来优化采场极限暴露面积。
(4)以本文的矿体赋存条件为例,在安全高效开采的前提下,设计安全系数为1.3时,通过回归函数曲线规律,确定卧虎山采场长30 m和40 m时的极限暴露面积为450 m2和600 m2,即最大的采场跨度为15 m。
参考文献
理想点法在采场结构参数优化中的应用
[J].
Application of ideal point method in mining stope structural parameters optimization
[J].
地下矿山采场结构参数的核主成分分析法优化
[J].
Optimization of structural parameters of stope in underground mine with kernel principal component analysis
[J].
采空区下方高应力环境下深部矿体回采时序研究
[J].
Study on mining sequence of deep orebody under high stress environment below goaf
[J].
金属矿山深部采场稳定性分析与结构参数优化
[J].
Stability analysis and parameter optimization of stope in deep metal mines
[J].
缓倾斜薄矿体采场极限暴露面积与参数优化
[J].
Maximum exposed area of stope with gently inclined thin orebody and parameters optimization
[J].
基于岩体时变力学参数的深部矿段回采顺序优化
[J].
Optimization of mining sequence based on rock mass time-varying mechanics parameters
[J].
采场暴露面积与地压活动规律初探
[J].
Discussion of laws between expoused stope area and ground pressure
[J].
毛公铁矿大结构参数无底柱分段崩落法多分段放矿实验
[J].
Multi-sublevel ore drawing test of non-pillar sublevel caving method with large structural parameters in Maogong iron mine
[J].
基于Mathews稳定图的采场暴露面积计算
[J].
Computation of stope exposure area based on Mathews stability diagram
[J].
基于Mathews稳定图法的采场暴露面积确定
[J].
Determination on the exposure area in stope based on Mathews stability graphic method
[J].
Mathew法在矿山深部采场稳定性分析中的应用
[J].
Application of Mathew method in the stability analysis of stope in deep mines
[J].
Experimental investigation on the strength characteristics of cement paste backfill in a similar stope model and its mechanism
[J].
Stability analysis of large-scale stope using stage subsequent filling mining method in Sijiaying iron mine
[J].
两中段开采的水平矿柱失稳影响因素分析与方案优化——以金川二矿区为例
[J].
Analysis of factors influencing horizontal pillar instability and optimization of two-level mining plans
[J].China Safety Science Journal
,
盘区隔离矿柱采场结构参数数值优化
[J].
Stope structural parameters of panel isolation pillar numerical optimization
[J].
基于采矿环境再造的开采顺序时变优化研究
[J].
Time-varying optimization study of mining sequence based on reconstructed mining environment
[J].
Estimation of the compressive strength of concrete under point load and its approach to strength criterions
[J].
Stability analysis of paste fill as stope wall using analytical method and numerical modeling in the Kencana underground gold mining with long hole stope method
[J].
Stability assessment of stope sequence scenarios in a diminishing ore pillar
[J].
Stability of undercut space in fragment orebody based on key block theory
[J].





 甘公网安备 62010202000672号
甘公网安备 62010202000672号