随着全球矿产资源开发力度的加大,采矿技术得到了快速发展,相关创新研究也在持续推进。经过长年开采,许多矿山面临着采矿回收率低及矿区污染严重等问题,而传统的采选冶工艺复杂,成本高,难以应对当前复杂多变的采矿形势。溶浸采矿法根据矿物的物理化学特性,有选择地溶解浸出并提取矿床中的有用组分,同时不会使周边围岩产生较大位移,是一种将采、选、冶工艺综合为一体的现代开采技术。前人对溶浸开采的研究主要集中在工艺技术及安全问题等方面,而在溶浸开采的浸出率优化方面开展的研究较少,田庆华等[1]采用人工神经网络对矿物的氧化浸出行为进行了预测,但预测精度有待提高。
近年来,神经网络在各个领域的应用研究逐渐兴起,发展非常迅速。BP神经网络可以通过模拟人类的一些智能脑神经思维来学习、训练和组织一些非线性动态问题的求解[4],但是由于初始权值和阈值随机性较大,导致神经网络训练过程中会出现低速收敛和精度不高的问题。因此本文通过BP神经网络训练溶浸开采矿区实例中影响矿物浸出率的参数数据,建立非线性映射关系,在前人研究的基础上,加入粒子群算法优化神经网络,能够提高预测精度,加快收敛速度,并对溶浸采矿浸出率预测问题进行优化改进,从而为当前矿区溶浸开采提供借鉴。
1 溶浸开采工艺及浸出率影响因素分析
1.1 溶浸开采工艺
溶浸开采方法主要有3种,分别是就地破碎浸矿法、原地浸矿法和堆浸法[5]。其中,就地破碎浸矿法与原地浸矿法相似,区别是前者需先利用爆破技术改变矿石的块度,再用溶浸液浸出矿石的有用成分,相比之下最常用的溶浸开采方法是堆浸法。在许多低品位矿床和尾矿处理中,相比其他采矿方法,溶浸开采方法的采矿成本更低,工艺简单,是当前应用最广泛的采矿方法。
1.2 溶浸开采浸出率的影响因素
近年来,已有学者对溶浸开采浸出率的影响因素进行分析。吴爱祥等[6]提出溶浸采矿的整个体系中主要的影响因素大致划分为3类,即生物因素、化学因素和物理因素。其中,生物因素涉及微生物种类、菌液浓度,以及氧气和二氧化碳的供给机制等;化学因素包括溶液pH值、Fe2+浓度、Fe3+浓度和溶液电位等,这些因素需要相互协调,赋予矿石最佳的浸出环境,才能达到最佳浸出率;物理因素关系到矿物的组成部分、颗粒的粒级分布、孔隙率和渗透压等,经研究发现矿石颗粒粗细对浸出率的影响并未呈现出正、负相关关系,矿石颗粒过粗或过细均不能达到最佳浸出效果。上述不同因素在溶浸开采过程中决定着整个浸出体系的温度场、浓度场和流体场相互作用的变化规律,更影响体系中的能量、动量转化与传递。
通过研究溶浸开采浸出率的影响因素发现,有些因素对应的参数与浸出率呈线性关系,可以根据实际情况均匀取值,如浸出的持续时间;有些因素则在不同环境下与浸出率呈非线性关系,如温度对浸出率的影响在一个温度区间内基本呈正相关,但并不是线性相关。若要预测上述影响因素对应的参数对整个溶浸开采浸出率的影响效应,运用常规的数学模型很难将这些非线性关系协同在一起,因此采用人工神经网络对其进行训练,探寻这些影响因素之间的相互关系。
2 BP神经网络
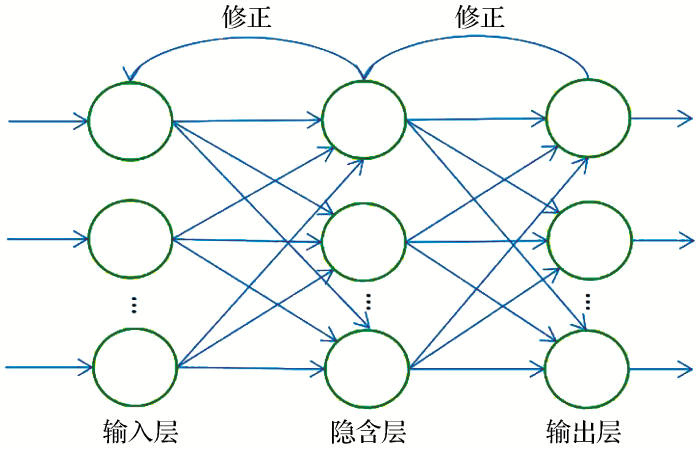
图1
从图1可以看出,BP神经网络在训练样本时,数据从输入层进入整个网络,经过隐含层的函数处理,最后由输出节点输出结果,可以设定输入向量为P,那么由神经网络处理后的输出向量为M,可表示为
式中:f为S型函数或其他线性函数;D为链接权值的矩阵;V为阈值向量。BP神经网络的典型构架可表示为3层感知模型[9]。其中,输入层中的输入值和输出值可分别表示为
式中:
当数据输出到达隐含层中时,神经网络会用函数进行处理分类,常见的函数有高斯函数,该层的输入值和输出值可分别表示为
式(4)中的高斯函数参数可以进行不断更新,更新方式可表示为
式中:t为迭代次数;λ为标准化常数;J为高斯核函数。
BP神经网络虽然可以处理非线性参数,但也存在一定的不足和局限性。比如:在样本的选择中,要求样本必须具有代表性,且如果样本数据参数较少,会导致BP神经网络在训练参数时无法优化到预期值。同时BP神经网络的初始权重随机性较大,因此常会出现训练过程无法高速收敛和结果精度低的现象。
3 粒子群算法优化的神经网络
3.1 粒子群算法
3.2 粒子群算法优化的BP神经网络模型
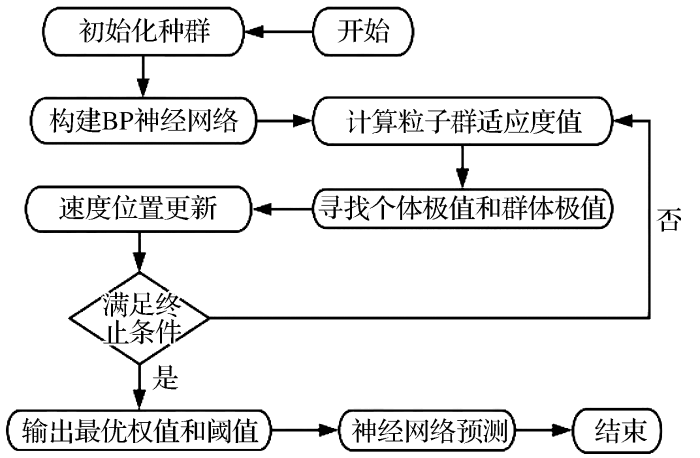
在BP神经网络中,权值和阈值的更新过程至关重要,是整个网络学习过程的主体因素,只要抓住对应的权值和阈值,利用粒子群算法中的粒子进行优化,就可以大幅提高神经网络的训练精度和预测能力。在神经网络的训练流程中,首先确定输入层、隐含层和输出层的具体结构参数;然后加入需要训练的输入数据集合,并给出期望输出值;同时加入粒子群优化算法,先初始化粒子群参数,包括粒子的速度位移向量、迭代次数、学习因子和惯性权重等,粒子数目一般由样本决定,通常取20~40个;学习因子对应的是粒子的自我学习能力,通常取2;惯性权重可以利用自适应法、线性递减法等设定,影响着粒子的速度更新能力[12,17]。由于优化过程存在误差,粒子群算法的适应性函数可以设置为神经网络的误差函数,整个优化过程的流程图如图2所示。
图2
优化过程如下:
(1)计算粒子的适应度值,并确定个体极值和全局最优极值。
(2)运用第3.1节中的式(10)~(13),对粒子的速度位移进行更新计算,得到粒子适应度更新值。
(3)根据新的适应度值重复更新粒子的个体极值和全局极值。
(4)反复迭代后,当误差达到期望值或达到设定的最大迭代次数时,结束粒子群算法,此时根据得到的最优结果设置新的神经网络权值与阈值。
4 基于粒子群优化的神经网络在溶浸开采浸出率预测中的应用
4.1 浸出率影响参数因子分析
本文开展的浸出率预测研究是以某矿山含锑硫化矿浸出过程为例。该含锑硫化矿采取原地浸矿法进行开采,其工艺流程如下:首先对矿床地质情况进行勘查,并划分合理的矿块;然后根据实际地形条件和设计好的参数布置注液孔,并注入浸矿剂,待浸矿剂均匀渗透后,矿床离子进入溶液混合后产出的浸出液汇入收液系统;最后进行分离沉淀等处理,从而得到所需的矿体成分。在含锑硫化矿的浸出过程中,通过氧化浸出试验得出影响浸出率的主导因素有温度、时间、液固比、搅拌速度和HCl浓度。其中,HCl浓度对含锑硫化矿的配位作用影响很大,故其影响效果最强;其次是温度,温度决定着反应速率,在一个温度段中温度与浸出率基本呈现非线性正相关,另外3个因素的影响也至关重要,所以将这5个因素作为神经网络结构的5个输入因子,考虑到这5个输入节点,参考文献[18]中输入层节点与隐含层节点关系的经验公式
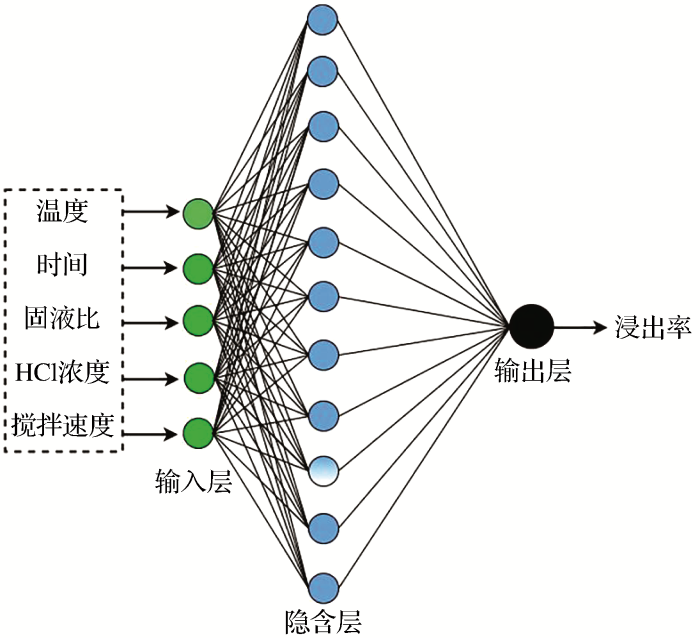
图3
图3
以浸出率为输出变量的PSO-BP神经网络结构图
Fig.3
Structure diagram of PSO-BP neural network with leach rate as output variable
4.2 神经网络模型的构建与预测结果
表1 训练组样本数据
Table 1
| 编号 | 温度/℃ | 时间/h | 固液比/(mL·g-1) | 搅拌速度/(r·min-1) | HCl浓度/(mol·L-1) | 浸出率/% |
|---|---|---|---|---|---|---|
| 1 | 85 | 1 | 10 | 300 | 4 | 48.17 |
| 2 | 85 | 5 | 8 | 300 | 4 | 84.73 |
| 3 | 85 | 3 | 10 | 500 | 3 | 85.06 |
| 4 | 85 | 4 | 10 | 300 | 3 | 83.75 |
| 5 | 85 | 3 | 10 | 300 | 4 | 76.75 |
| 6 | 85 | 1 | 10 | 300 | 3 | 46.25 |
| 7 | 85 | 5 | 10 | 300 | 1 | 12.03 |
| 8 | 85 | 1 | 10 | 500 | 3 | 58.32 |
| 9 | 85 | 4 | 10 | 900 | 3 | 90.93 |
| 10 | 85 | 5 | 10 | 300 | 3 | 90.50 |
| 11 | 85 | 3 | 10 | 300 | 2 | 51.19 |
| 12 | 85 | 5 | 6 | 300 | 4 | 76.00 |
| 13 | 85 | 3 | 10 | 300 | 1 | 10.75 |
| 14 | 85 | 2 | 10 | 300 | 4 | 64.25 |
| 15 | 85 | 4 | 12 | 300 | 4 | 91.08 |
| 16 | 85 | 1 | 10 | 300 | 2 | 36.75 |
| 17 | 85 | 2 | 10 | 300 | 1 | 10.24 |
| 18 | 85 | 1 | 12 | 300 | 4 | 59.07 |
| 19 | 85 | 1 | 6 | 300 | 4 | 44.14 |
| 20 | 85 | 5 | 10 | 900 | 3 | 93.75 |
| 21 | 85 | 1 | 10 | 900 | 3 | 74.21 |
| 22 | 85 | 1 | 10 | 300 | 4 | 47.25 |
| 23 | 85 | 2 | 10 | 900 | 3 | 88.00 |
| 24 | 85 | 3 | 12 | 300 | 4 | 87.78 |
| 25 | 85 | 2 | 8 | 300 | 4 | 63.65 |
| 26 | 85 | 5 | 10 | 300 | 4 | 93.06 |
| 27 | 85 | 5 | 12 | 300 | 4 | 93.58 |
| 28 | 85 | 4 | 10 | 300 | 4 | 86.25 |
| 29 | 85 | 1 | 10 | 700 | 3 | 63.53 |
| 30 | 85 | 3 | 6 | 300 | 4 | 65.57 |
| 31 | 85 | 5 | 6 | 300 | 4 | 76.00 |
| 32 | 85 | 4 | 10 | 300 | 1 | 11.01 |
| 33 | 85 | 4 | 10 | 500 | 3 | 89.96 |
| 34 | 85 | 5 | 10 | 300 | 4 | 93.06 |
| 35 | 85 | 2 | 10 | 500 | 3 | 72.67 |
| 36 | 85 | 2 | 10 | 300 | 4 | 66.20 |
| 37 | 85 | 5 | 10 | 500 | 3 | 93.24 |
| 38 | 85 | 2 | 10 | 700 | 3 | 74.61 |
| 39 | 85 | 4 | 10 | 700 | 3 | 91.48 |
| 40 | 85 | 5 | 10 | 300 | 2 | 66.25 |
式中:
式中:P为样本的总数;N为输出节点数;
表2 预测组样本数据
Table 2
| 编号 | 温度/℃ | 时间/h | 固液比/(mL·g-1) | 搅拌速度/(r·min-1) | HCl浓度/(mol·L-1) | 浸出率/% |
|---|---|---|---|---|---|---|
| 1 | 85 | 4 | 8 | 300 | 4 | 80.83 |
| 2 | 85 | 5 | 10 | 700 | 3 | 93.55 |
| 3 | 85 | 3 | 10 | 300 | 4 | 78.06 |
| 4 | 85 | 2 | 10 | 300 | 4 | 66.02 |
| 5 | 85 | 4 | 10 | 300 | 3 | 83.75 |
| 6 | 85 | 3 | 10 | 300 | 3 | 76.75 |
| 7 | 85 | 3 | 10 | 300 | 4 | 78.06 |
| 8 | 85 | 3 | 10 | 700 | 3 | 85.26 |
当完成数据预处理后,初始化粒子群算法的参数,设定粒子数目为30,学习因子为2,粒子的速度
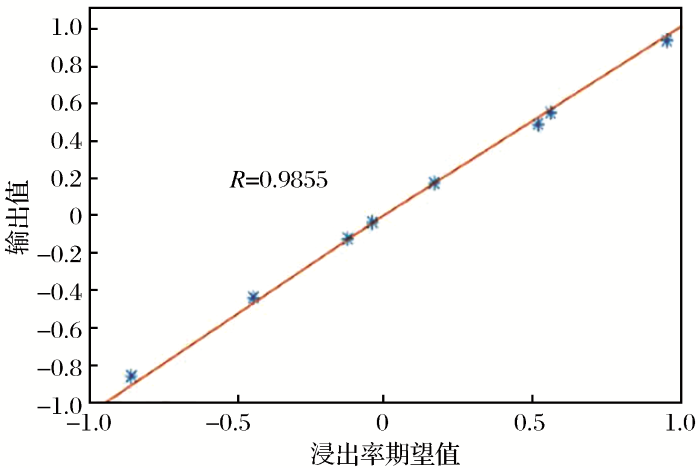
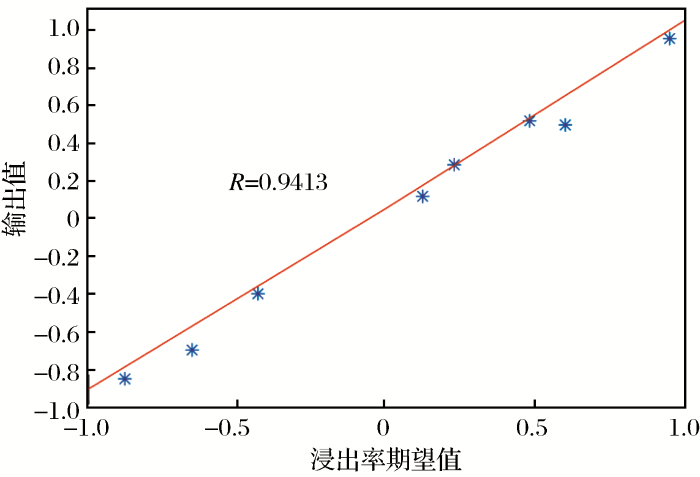
运用MATLAB软件[21]构建和优化神经网络,在不断的迭代中,神经网络的权值、阈值也不断更新使神经网络的精度达到预期精度,由于整个过程受参数设置、训练方法和函数设置等因素的影响,因此需要对建立的神经网络模型进行检测。为了对比粒子群优化与未优化的BP神经网络预测结果的精度,将表2中的预测样本数据分别代入训练好的经粒子群优化的神经网络模型和未优化的BP神经网络模型中,所得出的预测值与预测样本中的期望值均做归一化处理,并分别作出2种模型的线性回归曲线(图4,图5)。线性回归曲线的横纵坐标分别是浸出率的期望值和实际输出值,通过线性回归拟合点近似连线的斜率可以很好地反映这2个数值的拟合近似程度,斜率越接近1则实际输出值越接近期望值。最终可以看出,粒子群优化的神经网络模型预测的浸出率结果与实际值的线性回归曲线斜率更接近1,即粒子群优化的预测精度较未优化的BP神经网络高。
图4
图4
粒子群优化的神经网络浸出率预测组线性回归曲线
Fig.4
Linear regression curve of particle swarm optimization neural network leach rate prediction group
图5
图5
BP神经网络浸出率预测组的线性回归曲线
Fig.5
Linear regression curve of BP neural network leach rate prediction group
表3 BP神经网络和PSO-BP神经网络模型预测结果统计
Table 3
| 序号 | 实际值 | BP神经网络预测 | PSO-BP神经网络预测 | ||
|---|---|---|---|---|---|
| 预测值 | 相对误差 | 预测值 | 相对误差 | ||
| 1 | 80.83 | 79.45 | -0.0171 | 80.45 | -0.0047 |
| 2 | 93.55 | 92.70 | -0.0093 | 93.21 | -0.0036 |
| 3 | 78.06 | 78.21 | 0.0019 | 78.09 | 0.0038 |
| 4 | 66.02 | 66.92 | 0.0136 | 66.13 | 0.0017 |
| 5 | 83.75 | 83.05 | -0.0083 | 83.40 | -0.0042 |
| 6 | 76.75 | 74.98 | -0.0231 | 75.91 | -0.0109 |
| 7 | 78.06 | 78.87 | 0.0104 | 78.76 | 0.0089 |
| 8 | 85.26 | 85.30 | 0.0004 | 85.29 | 0.0004 |
表4 BP神经网络、PSO-BP神经网络模型预测结果误差分析
Table 4
| 指标 | BP神经网络模型 | PSO-BP神经网络模型 |
|---|---|---|
| 最大相对误差 | 0.0231 | 0.0109 |
| 最小相对误差 | 0.0004 | 0.0004 |
| 平均相对误差 | 0.0118 | 0.0057 |
| 样本方差 | 0.9675 | 0.1985 |
5 结论
(1)溶浸开采过程中的浸出率受诸多因素的影响,在含锑硫化矿的浸出过程中,浸出率主要受温度、反应时间、固液比、搅拌速度和HCl浓度的影响,其中HCl浓度占主导因素,其次为温度、搅拌速度、固液比和反应时间,其影响占比依次减小,这些因素相互作用,协同影响着浸出率。
(2)采用粒子群算法对BP神经网络进行优化,有效地提高了神经网络对浸出率的预测精度,预测结果的相对误差整体降低,模型对应结果的方差也相对降低,表明经粒子群优化的神经网络模型的预测更精确、更稳定。
(3)在溶浸开采过程中,影响浸出率的因素非常繁杂,部分影响因素与浸出率多呈非线性关系,因此利用粒子群算法优化BP神经网络模型,以此模型来模拟预测受多因素影响的溶浸开采浸出率是一种精准且有效可行的预测方法。
参考文献
基于人工神经网络模型的含锑硫化矿氧化浸出行为预测
[J].
Prediction of oxidation leaching behavior of antimony-containing sulfide ore based on artificial neural network model
[J].
溶浸采矿最优化问题分析与探讨
[J].
Analysis and discussion on optimization of leaching mining
[J].
溶浸采矿技术研究应用现状综述
[J].
Review of research and application of leaching mining technology
[J].
一种基于粒子群优化算法的神经网络训练方法
[J].
A neural network training method based on particle swarm optimization
[J].
溶浸采铀(矿)
[M].
Leaching Uranium(Ore)
[M].
溶浸采矿技术的进展与展望
[J].
Development and prospect of leaching mining technology
[J].
人工神经网络的发展及应用
[J].
Application and prospect of artificial neural network
[J].
人工神经网络
[M].
Artificial Neural Network
[M].
Optimal parameters selection for BP neural network based on particle swarm optimization:A case study of wind speed forecasting
[J].
基于人工神经网络的空调房间热环境参数的优化组合
[D].
Combination of Thermal Environment Parameters of Air-Conditioned Rooms Based on Artificial Neural Network
[D].
神经网络系统理论
[M].
Neural Network System Theory
[M].
基于灰色关联分析的PSO-BP算法预测矿震危险性
[J].
Prediction of PSO-BP algorithm in risk prediction of mine earthquake based on grey correlation analysis
[J].
基于改进的QPSO-BP算法的铀价格预测模型及应用
[J].
Uranium price forecasting model based on BP improved by QPSO and its application
[J].
基于粒子群优化BP神经网络的高校科研管理评估研究
[J].
Research on university scientific research management evaluation based on particle swarm optimization algorithm and BP neural network
[J].
基于粒子群神经网络的软岩巷道变形预测
[J].
Prediction of soft rock roadway deformation based on particle swarm optimization neural network
[J].
基于PSO算法的BP神经网络在边坡稳定性评价中的应用
[J].
Application of BP neural network in slope stability evaluation on the basis of PSO algorithm
[J].
基于PSO-BP神经网络的网络流量预测与研究
[J].
Prediction and research on network traffic based on PSO-BP neural network
[J].
矿震地震活动响应规律及其危险性预测研究
[D].
Research on Seismic Aactivity Response Law and Hazard Prediction of Mine Earthquakes
[D].
Fatigue analysis of floating wind turbine support structure applying modified stress transfer function by artificial neural network
[J].
BP神经网络在状态监测数据趋势预测中的应用
[J].
Application of BP ANN in predicting condition monitoring data
[J].





 甘公网安备 62010202000672号
甘公网安备 62010202000672号