充填采矿法符合建设绿色矿山的要求,该方法在提高资源回收率、控制采场地压以及减少矿山开采对地表环境的破坏等方面具有一定的优势,已被推广应用于全世界众多地下矿山(Ghirian et al.,2013;Wu et al.,2015)。充填体的损伤及强度准则是充填采矿法研究最基本的内容。充填体作为一种复合材料,其内部含有大量的微裂隙和微孔洞。因此,确定充填体材料在荷载下的力学性能及损伤特性对地下采空区的安全性具有重要意义。
国内外学者对充填体材料力学特性和损伤本构模型开展了大量的研究工作。Zhou et al.(2021)研究了钽铌矿尾砂胶结充填体在单轴压缩条件下的力学特性及损伤演化规律。Hou et al.(2020)研究了渗透压力对充填体力学特性的作用规律,分析了渗流—应力耦合作用下充填体的损伤机理。程爱平等(2019)对不同尺寸充填体试件开展了单轴压缩试验,通过分析加载过程中试件产生的声发射信号,以及试验前后充填体试件的超声波波速变化规律,得出了不同尺寸胶结充填体试件的损伤演化规律。易雪枫等(2020)采用单轴抗压试验和CT扫描技术,对废石含量不同的金属矿山尾废胶结充填体的损伤破裂演化过程进行了可视化和数字化研究,结果表明充填体中最薄弱的部分为基质—块体交界面,该交界面的损伤开裂控制了充填体试样裂纹扩展路径。刘志祥等(2006)和赵树果等(2017)通过开展不同灰砂配比的尾砂胶结充填体力学试验,研究了相应充填体的损伤破坏并建立了损伤本构模型。王勇等(2019)对不同初始温度下的全尾砂胶结充填体进行单轴抗压试验,建立了全尾砂充填体的温度—试件耦合损伤本构模型,并将此模型嵌入Comsol数值模拟软件进行单轴抗压数值模拟试验,模拟结果与试验结果较为吻合,从而验证了所建立损伤本构模型的可行性。汪杰等(2019)对不同分层充填体进行了力学特性试验,提出了初始分层损伤、荷载损伤和总损伤的概念,并结合损伤力学理论,建立了考虑分层效应的充填体损伤本构模型。上述学者在充填体材料力学特性及损伤特性方面取得的研究成果对于保持采空区结构的稳定性具有重要的指导意义。然而充填体是一种多相复合材料,其内部含有大量的微孔洞和微裂隙,在单轴荷载初始阶段存在微孔洞和微裂隙的压密,因此经典损伤本构模型无法很好地模拟这个过程。
结合前人开展的充填体力学试验研究,基于统计损伤理论、最大拉应力准则和应变等效假说,推导了充填体材料在单轴荷载下的经典损伤本构模型,同时鉴于充填体试件在加载初期存在压密行为,建立了考虑压密过程的修正损伤本构模型。通过拟合几组试验数据,并与经典损伤本构模型进行对比分析,验证了本文充填体损伤本构模型的可靠性,并进一步研究了拟合参数变化对修正损伤本构模型曲线形状的影响。
1 统计损伤本构模型
1.1 充填体试件在单轴压缩下的变形特征
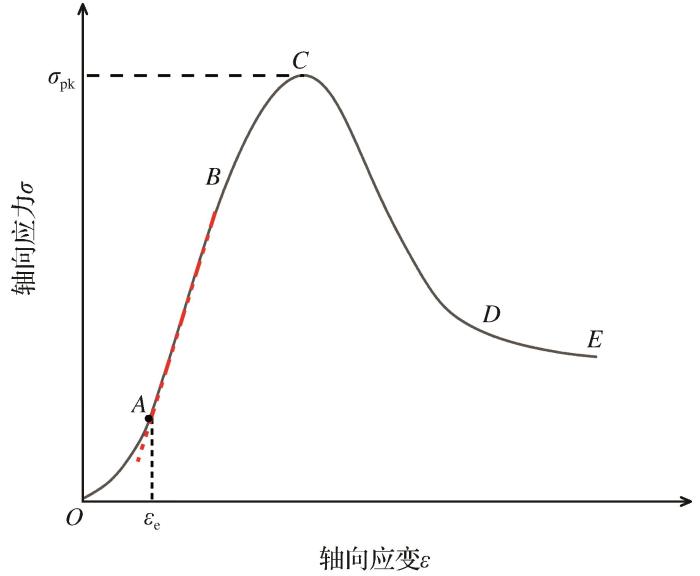
充填体材料在单轴压缩条件下的应力—应变曲线可划分为5个阶段,如图1所示,分别是初始压密阶段(OA)、弹性变形阶段(AB)、应变硬化阶段(BC)、应变软化阶段(CD)和残余强度阶段(DE)。虽然不同类型的充填体材料在单轴压缩试验中的应力—应变曲线不尽相同,但其主要特征相似,如:初始阶段产生压密过程,弹性阶段弹性模量保持一致,应变硬化阶段弹性模量逐渐减小,峰后阶段应力快速衰减,以及由于破碎面的摩擦,试件在加载末尾存在残余阶段。
图1
图1
充填体材料在单轴压缩条件下的经典应力—应变曲线
Fig.1
Typical stress-strain curve of backfill material under the uniaxial compression condition
1.2 充填体试件经典损伤本构模型的推导
充填体材料中存在大量的微孔洞和微裂隙等缺陷,这些缺陷在外荷载作用下逐渐扩展和延伸,最终导致材料的破坏,材料的损伤是一个累积的过程(Justo et al.,2017;Wang et al.,2019a;Lin et al.,2015;Wang et al.,2019b)。但这些微缺陷的位置、尺寸、强度和刚度等特性无法准确预测。Weibull分布是在研究材料强度与疲劳寿命时提出的,在开展材料力学试验时,Weibull分布得到广泛的应用(杨圣奇等,2004;张社荣等,2019;张超等,2019),其微单元强度的概率密度函数可表示为
式中:
在单轴荷载下充填体材料内部的损伤可以定义为失效单元数量与总单元数量的比值,当充填体材料荷载至某一应变水平ε时,充填体材料内部的损伤可表示为
式中:充填体损伤变量D的值域为(0,1),其值域范围对应充填体材料从未受损到完全受损的破坏状态。
Lemaitre(1972)提出了应变等效假说。其假设材料损伤仅通过有效应力来改变应变行为,该假说被广泛应用于各种加载条件下的材料损伤领域的研究(Huang et al.,2018;Voyiadjis et al.,2008;Ren et al.,2013;Al-Rub et al.,2010)。根据应变等效假说,Lemaitre(1985)建立了单轴加载损伤本构模型,结合
式中:σ为轴向应力;E为充填体试件的弹性模量。
1.3 充填体试件经典损伤本构模型的修正
上述经典损伤本构方程的建立中,没有考虑充填体材料在初始阶段的压密过程。如图1所示,充填体材料内部存在许多微孔和裂纹等缺陷,这些初始缺陷在加载初期被逐渐压实,因此应力—应变曲线在加载初始阶段呈现明显的凹陷。为了准确地模拟充填体试件在初始阶段的压密过程,提出压密系数α,其为无量纲的常数,在试件荷载未到达弹性变形阶段之前,其数值随着应变的增大呈对数函数形式增大。当试件荷载到应变为εc时,即试件进入弹性变形阶段的初始点,此时压密系数α的数值为1。
式中:n为通过试验数据拟合得到的常数;εc值对应充填体材料压密阶段末尾的应变。在εc点之前,压密系数α呈对数函数形式增大,而在εc点之后,压密系数α为1。
εc值的确定方法如下:①作出试验数据应力—应变曲线弹性变形阶段的线性拟合曲线;②将应力—应变弹性变形阶段的线性拟合曲线向下延伸,直至与应力—应变曲线分离,如图2所示;③找出应力—应变曲线与线性拟合曲线的分离点,即为εc。
图2
压密系数α定义为充填体试件应力—应变曲线的斜率与弹性模量之比,其数值随应变的增大呈对数函数增大的趋势。将该系数引入
式中:n、a和m为常数,其数值可以通过拟合试验数据获得。
2 模型验证与拟合参数分析
2.1 模型验证
通过对3种不同试验结果进行拟合,并与经典损伤本构模型进行对比分析,来验证修正损伤本构模型的可靠性。具体结果如下:
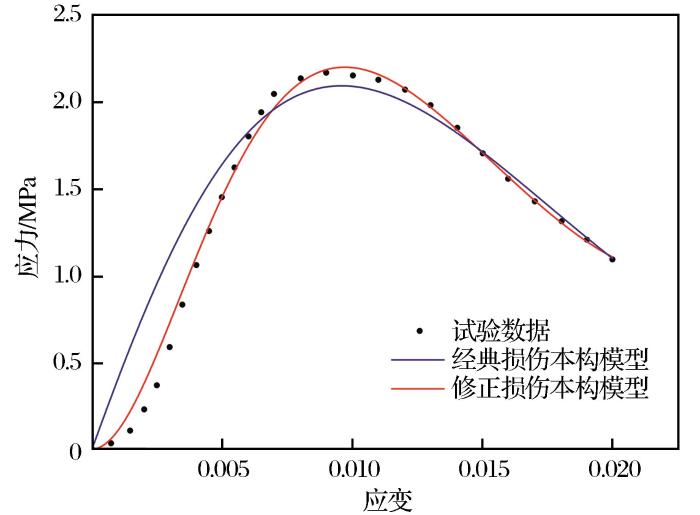
(1)刘艳章等(2019)对尾砂胶结充填体进行了单轴压缩试验,采用细粒级大冶铁矿全尾砂制备了尾砂胶结充填体。在试件制备过程中,采用325#普通硅酸盐水泥作胶凝剂,全尾砂中值粒径为28.6 μm,灰砂比为1∶6,所制备的试件尺寸为Φ50 mm × 100 mm。制备好的充填体试样在温度为(20±2)℃、相对湿度为(95±1)%的环境中养护28 d后采用WAW-300电液伺服万能试验机进行单轴压缩试验。试验加载方式采用力控制,加载速率为0.02 kN/s。分别采用经典损伤本构模型和修正损伤本构模型对试验数据进行拟合,拟合曲线如图3所示。由图3可知,修正损伤本构模型的拟合优度R2=0.990,拟合效果优于经典损伤本构模型。拟合参数及相关的物理力学参数见表1。
图3
图3
单轴荷载下尾砂胶结充填体应力—应变试验数据及拟合曲线
Fig.3
Stress-strain test data and fitting curves of cemented tailings backfill under uniaxial load
表1 尾砂胶结充填体拟合参数及相关物理力学参数
Table 1
| 参数 | 数值 | 参数 | 数值 |
|---|---|---|---|
| n | 0.858 | εc /(×10-2) | 0.326 |
| a /(×10-2) | 0.584 | E/GPa | 0.413 |
| m | 1.242 | R2 | 0.990 |
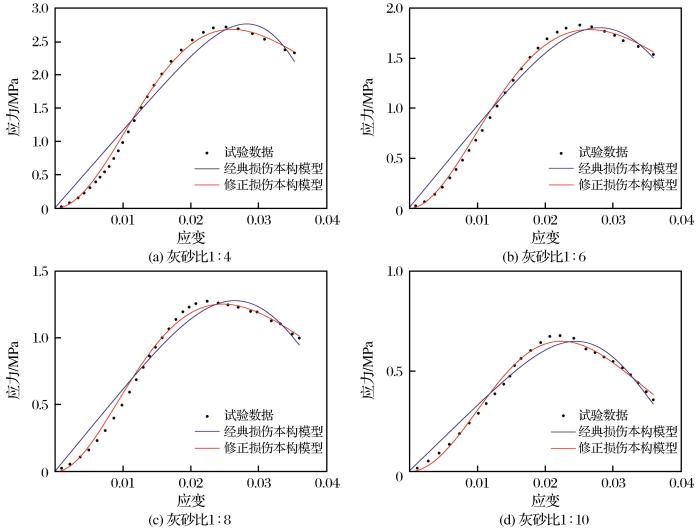
(2)柯愈贤等(2019)对不同灰砂比全尾砂充填体进行单轴压缩试验。采用普通硅酸盐水泥与某矿全尾砂制备了质量分数为68%而灰砂比不同的全尾砂充填体试块。试块在恒温养护箱(20 ℃)养护28 d后在MTS Landmark试验机上进行单轴荷载试验。分别采用经典损伤本构模型和修正损伤本构模型对试验结果进行拟合,拟合曲线如图4所示。
图4
图4
不同灰砂比全尾砂充填体单轴压缩试验数据及拟合曲线
Fig.4
Uniaxial compression test data and fitting curves of full tailings backfill with different cement-sand ratios
表2 不同灰砂比全尾砂充填体拟合参数及相关物理力学参数
Table 2
| 灰砂比 | n | a /(×10-2) | m | εc /(×10-2) | E /GPa | R2 |
|---|---|---|---|---|---|---|
| 1∶4 | 0.756 | 1.876 | 1.529 | 1.1561 | 0.188 | 0.995 |
| 1∶6 | 0.857 | 1.754 | 1.339 | 0.894 | 0.107 | 0.996 |
| 1∶8 | 0.834 | 1.660 | 1.366 | 0.934 | 0.089 | 0.993 |
| 1∶10 | 0.837 | 1.929 | 1.757 | 0.934 | 0.038 | 0.991 |
图5
图5
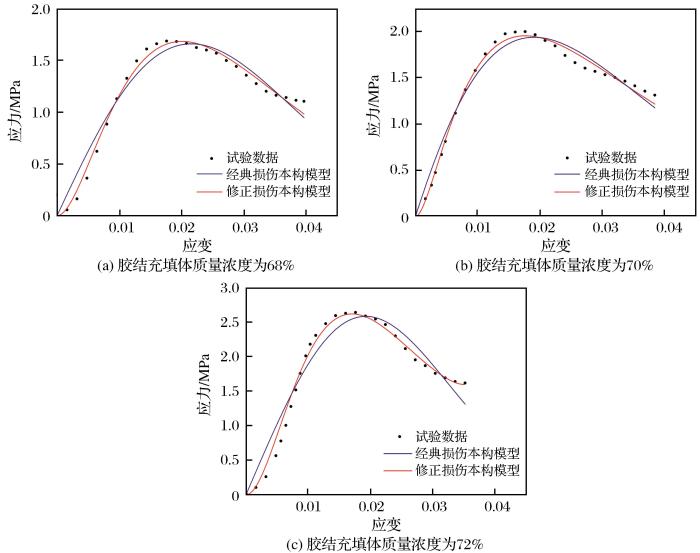
不同质量浓度尾砂胶结充填体单轴压缩试验数据及拟合曲线
Fig.5
Uniaxial compression test data and fitting curves of cemented tailings backfill with different mass concentrations
表3 不同质量浓度尾砂胶结充填体拟合参数及相关物理力学参数
Table 3
| 胶结充填体 质量浓度/% | n | a/ (×10-2) | m | εc /(×10-2) | E/GPa | R2 |
|---|---|---|---|---|---|---|
| 68 | 1.180 | 1.086 | 0.972 | 0.481 | 0.152 | 0.988 |
| 70 | 1.371 | 0.687 | 0.754 | 0.207 | 0.188 | 0.993 |
| 72 | 0.861 | 0.907 | 1.147 | 0.533 | 0.307 | 0.982 |
由上述3组试验数据的拟合结果可得:修正损伤本构模型可以较好地模拟充填体试件在单轴荷载下应力—应变变化的整个过程,且试验数据与所建模型基本吻合;与经典损伤本构模型相比,修正损伤本构模型可以模拟充填体试件在初始阶段的压密过程。这充分说明了所建损伤本构模型的可靠性。
2.2 拟合参数对拟合曲线形状的影响
参数n、a和m影响拟合曲线的几何尺度和形状,拟合参数的准确性对充填体损伤本构模型在单轴压缩载荷作用下的适用性具有重要意义。本文采用控制变量法分析参数变化对拟合曲线形状的影响。为了减少工作量,仅选取柯愈贤等(2019)试验数据的拟合曲线进行分析。其中,该类型充填体试件试验数据拟合参数的拟合结果标准误差分别为0.173346、0.205529e-2和0.202294。在参数误差范围内,分析参数变化对拟合曲线几何形状的影响。
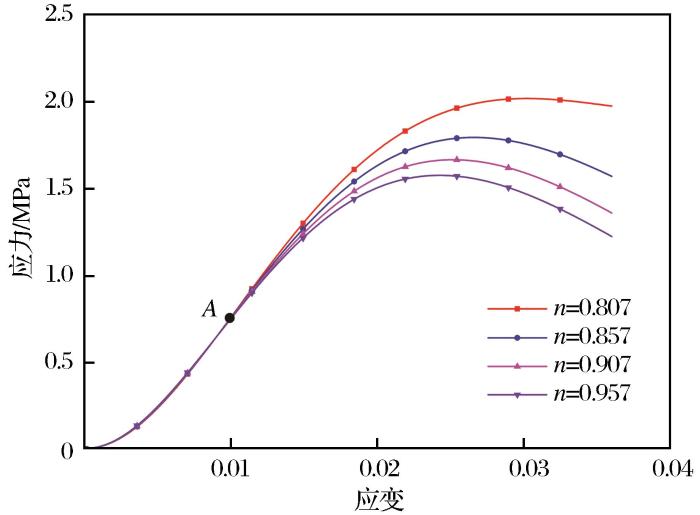
(1)参数n对拟合曲线几何尺度和形状的影响。当分析参数n值对拟合曲线几何尺度和形状的影响时,保持参数a(0.01754)和m(1.529)的值不变,n值分别取0.807、0.857、0.907和0.957(在标准差范围内对参数n进行等差数列取值,公差为0.050),得到4条不同的应力—应变曲线,如图6所示。从图6中可以看出,不同n值对应的4条应力—应变曲线在初始阶段有一个分离点A。在起始点与分离点之间,4条应力—应变曲线几乎是重叠的,说明在这一阶段参数n值的变化几乎不影响曲线的几何形状。在A点之后,不同参数n值对应的应力—应变曲线逐渐分离,且曲线的应力随着n的增大而减小。峰值点之后,4条不同参数n值对应的曲线的应力逐渐减小,且应力的衰减速率随着n值的增大而增大。
图6
图6
参数n对拟合曲线形状的影响
Fig.6
Effect of parameters n on the shape of the fitting curves
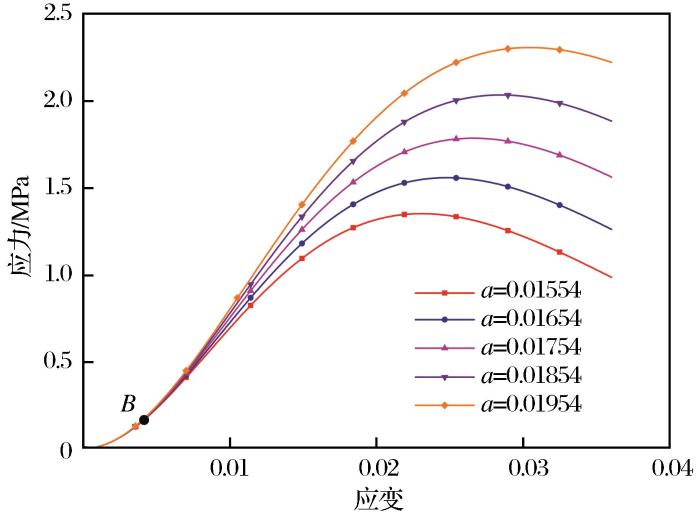
(2)参数a对拟合曲线几何尺度和形状的影响。当分析参数a值对拟合曲线几何尺度和形状的影响时,保持参数n(0.857)和m(1.339)的值不变,a值分别取0.01554、0.01654、0.01754、0.01854和0.01954(在标准差范围内对参数a进行等差数列取值,公差为0.001),得到5条不同的应力—应变曲线,如图7所示。从图7中可以看出,不同a值对应的5条应力—应变曲线在初始阶段有一个分离点B。在起始点与分离点之间,5条不同参数a值对应的应力—应变曲线几乎是重叠的,说明在这一阶段参数a值的变化几乎不影响曲线的几何形状。在B点之后,不同参数a值对应的应力—应变曲线逐渐分离,且曲线的应力随着a值的增大而增大。峰值点之后,5条不同参数a值对应的曲线的应力逐渐减小。此处与n值变化对应的曲线不同之处是:①a值变化对应的应力—应变曲线重叠部分较少(起始点与分离点B之间);②峰值点后不同a值对应的曲线应力的衰减速率几乎相同。
图7
图7
参数a对拟合曲线形状的影响
Fig.7
Effect of parameters a on the shape of the fitting curves
(3)参数m对拟合曲线几何尺度和形状的影响。当分析参数m值对拟合曲线几何尺度和形状的影响时,保持参数n(0.857)和a(1.754)的值不变,m值分别取1.139、1.239、1.339、1.439和1.539(在标准差范围内对参数m进行等差数列取值,公差为0.1),得到5条不同的应力—应变曲线,如图8所示。从图中可以看出,不同m值对应的应力—应变曲线在初始阶段几乎是重叠的,说明参数m的变化不影响初始阶段曲线的形状。不同m值对应的应力—应变曲线在C点分离,在D点再次相交。在分离点C与交点D之间,应力—应变曲线的应力随着m值的增大而增大。在交点D之后,应力—应变曲线的应力随着m值的增大而减小。峰值点之后,随着m的增加,应力的衰减速率也随之增大。
图8
图8
参数m对拟合曲线形状的影响
Fig.8
Effect of parameters m on the shape of the fitting curves
3 结论
基于统计损伤理论、最大拉应力准则和应变等效假说,推导了充填体材料在单轴荷载下的经典损伤本构模型。根据充填体材料的应力—应变曲线在初始荷载下存在压密阶段,提出了压密系数并将其引入经典损伤本构模型中,建立了充填体试件在单轴荷载下的修正损伤本构模型。
通过拟合几组试验数据,获得了修正损伤本构模型的拟合曲线,将修正损伤本构模型与经典损伤本构模型进行对比分析,验证了本文所构建的充填体损伤本构模型的可靠性,并进一步研究了模型参数变化对修正损伤本构模型曲线形状的影响。得出如下结论:
(1)修正损伤本构模型拟合曲线很好地体现了单轴荷载下充填体材料的应力—应变变化的初始压密阶段、弹性变形阶段、应变硬化阶段、应变软化阶段和残余强度阶段,且3组试验数据拟合优度R2>0.98,说明修正损伤本构模型的拟合效果比经典损伤本构模型的效果好。
(2)与经典损伤本构模型相比,修正损伤本构模型很好地模拟了充填体材料在单轴荷载下初始阶段的压密行为,说明修正损伤本构模型比经典损伤本构模型更加可靠。
(3)根据试验数据拟合结果的标准误差,在误差范围内对拟合参数进行等差数列取值,研究不同参数的变化对拟合曲线形状的影响,结果显示不同参数对拟合曲线形状产生的影响不同,参数的准确性对充填体损伤本构模型在单轴压缩载荷作用下的适用性具有重要物理意义。
http://www.goldsci.ac.cn/article/2021/1005-2518/1005-2518-2021-29-4-555.shtml
参考文献
Computational applications of a coupled plasticity-damage constitutive model for simulating plain concrete fracture
[J].
Study on size effect of damage evolution of cemented backfill
[J].
Coupled thermo-hydro-mechanical-chemical behaviour of cemented paste backfill in column experiments.Part I:Physical,hydraulic and thermal processes and characteristics
[J].
Mechanical properties and meso-structure response of cemented gangue-fly ash backfill with cracks under seepage-stress coupling
[J].
A statistical damage constitutive model under freeze-thaw and loading for rock and its engineering application
[J].
Notch effect on the fracture of several rocks:Application of the theory of critical distances
[J].
Strength determination of crude tailings backfill in deep mine based on non-linear constitutive model
[J].
Evaluation of dissipation and damage in metals submitted to dynamic loading
[J].
A continuous damage mechanics model for ductile fracture
[J].
Three-dimensional effects in a flattened Brazilian disk test
[J].
Analysis of damage variables and specific energy evolution for cemented tailings backfill under uniaxial compression condition
[J].
On damage model of cemented tailings backfill and its match with rock mass
[J].
A unified dynamic model for concrete considering viscoplasticity and rate-dependent damage
[J].
A comparative study of damage variables in continuum damage mechanics
[J].
Damage constitutive model and strength criterion of horizontal stratified cemented backfill
[J].
Seismic response of tunnel lining structure in a thick expansive soil stratum
[J].
Numerical analysis of fiber-reinforced soils based on the equivalent additional stress concept
[J].
Damage constitutive model of cemented tailing paste under initial temperature effect
[J].
Coupled effects of cement type and water quality on the properties of cemented paste backfill
[J].
Statistical constitutive model for rock damage under uniaxial compression and its experimental study
[J].
Experimental study on the fracture evolution of cemented waste rock-tailings backfill (CWRB) of metal ore using in-situ CT scanning
[J].
Study of damage constitutive model of brittle rock considering post-peak stress dropping rate
[J].
Dynamic mechanical property analysis of roller-compacted concrete and damage constitutive model establishment
[J].
Experimental study on AE characteristics of cemented tailings backfill failure process with different concentration
[J].
Study on damage model of backfill based on Weibull distribution under uniaxial compression
[J].
On acoustic emission characteristics,initiation crack intensity,and damage evolution of cemented paste backfill under uniaxial compression
[J].
胶结充填体损伤演化尺寸效应研究
[J].
基于全尾砂充填体非线性本构模型的深井充填强度指标
[J].
单轴压缩条件下尾砂胶结充填体的损伤变量与比能演化
[J].
尾砂胶结充填体损伤模型及与岩体的匹配分析
[J].
水平分层胶结充填体损伤本构模型及强度准则
[J].
初始温度条件下全尾胶结膏体损伤本构模型
[J].
单轴压缩下岩石损伤统计本构模型与试验研究
[J].
金属矿尾废胶结充填体破裂演化过程原位CT扫描试验研究
[J].
考虑峰值后区应力跌落速率的脆岩损伤本构模型研究
[J].
碾压混凝土的动态力学特性分析及损伤演化本构模型建立
[J].
不同浓度的尾砂胶结充填体破坏过程声发射特性试验研究
[J].
基于Weibull分布的充填体单轴压缩损伤模型研究
[J].







 甘公网安备 62010202000672号
甘公网安备 62010202000672号