单向受限应力下镐型截齿破岩特性及其影响因素分析

doi:10.11872/j.issn.1005-2518.2021.05.009

单向受限应力下镐型截齿破岩特性及其影响因素分析

唐宇^,, 王少锋^,

中南大学资源与安全工程学院，湖南长沙 410083

Analysis on Rock Breakage Characteristic and Its Influence Factors of Conical Pick Under Uniaxial Confining Stress

TANG Yu^,, WANG Shaofeng^,

School of Resources and Safety Engineering，Central South University，Changsha 410083，Hunan，China

通讯作者: 王少锋（1989-），男，河南洛阳人，特聘教授，硕士生导师，从事深部硬岩破碎与岩体灾害防控方面的研究工作。sf.wang@csu.edu.cn

收稿日期: 2020-12-29 修回日期: 2021-04-06

基金资助:

国家自然科学基金项目“深部高应力下镐形截齿破岩特性及诱导调控机理”. 51904333
“深部硬岩可切割性综合表征与靶向诱导致裂研究”. 52174099

Received: 2020-12-29 Revised: 2021-04-06

作者简介 About authors

唐宇（1998-），男，湖南邵阳人，硕士研究生，从事深部硬岩破碎方面的研究工作195512136@csu.edu.cn , E-mail：195512136@csu.edu.cn

摘要

基于刀具破岩的非爆机械化开采有望成为深部矿山开采的主要替代方法之一。矿岩可切割性是制约刀具破岩的关键因素，其受到受限应力条件和岩石性质的影响。因此，研究不同种类岩石在不同受限应力条件下的可切割性，可为机械刀具破岩提供理论依据和关键技术参数支撑。首先在不同受限应力条件下，对花岗岩、大理岩、红砂岩和磷矿石进行了截齿破岩试验。然后，以试验结果为基础，对脆性指数、受限应力条件与截齿破岩峰值载荷和破岩比能之间的关系分别进行了回归分析。最后，利用熵权法评价了岩石强度特性和受限应力条件对截齿破岩峰值载荷和破岩比能的影响权重。结果表明：所建立的回归模型具有良好的预测精度，单向受限应力和脆性指数对截齿破岩峰值载荷和破岩比能的影响均呈非线性变化；单向受限应力和岩石强度特性对截齿破岩性能均有显著影响，且单向受限应力的影响权重略大于岩石强度特性。研究结果可为深部矿山非爆机械化开采可行性判别以及破岩参数设计提供理论依据。

关键词： 深部开采 ; 非爆机械化开采 ; 截齿破岩 ; 单向受限应力 ; 可切割性 ; 熵权法

Abstract

With the gradual depletion of shallow resources，deep mining is an inevitable trend. However，the traditional drilling and blasting method has been difficult to meet the requirements of continuous，large-scale，safe，efficient and green resource exploitation in deep mining. Non-explosive mechanized mining based on cutting tool rock breaking will be one of the main alternative methods for deep mining. The cuttability of deep hard rock is the key factor to determine the non-explosive mechanical rock breaking. Therefore，we carried out the rock breaking experiment by conical pick and studied the rock cuttability under different confining pressures and rock properties. The experiment was performed on the TRW-3000 true triaxial electro-hydraulic servo test system designed and manufactured by Central South University. The system can simulate the stress conditions under uniaxial，biaxial and triaxial confining stress conditions. The maximum static load applied in X，Y and Z directions is 2 000 kN，2 000 kN and 3 000 kN respectively. The rock samples utilized in this experiment are granite，marble，red sandstone and phosphate rock，all of which are cubic rock samples with the size of 100 mm×100 mm×100 mm. In order to simulate the stress on the pillar to be mined，uniaxial confining pressure was applied to the rock sample on the Y-axis. The range of confining pressure of granite and marble is 0~120 MPa，that of red sandstone is 0~90 MPa，and that of phosphate rock is 0~100 MPa. Then，the rock breakage load is applied to rock specimen by conical pick through Z-axis，so as to cut the rock sample vertically. In the whole experiment process，the system recorded the load change on rock in the loading process automatically. According to the curve change，the peak indentation force and corresponding penetration depth of the pick were obtained，and the cutting work required for rock breaking could be obtained. Then，the specific energy of rock breaking could be calculated according to the cutting work and the volume of the spalling rock block. In addition，according to the ISRM standards，the uniaxial compressive strength and tensile strength of four types of rocks were obtained by uniaxial compression test and Brazilian splitting test. Then，the brittleness index of rock was obtained. The uniaxial compressive strength，brittleness index，peak indentation force and specific energy were normalized. Through regression analysis，the regression models of the relationships among the peak indentation force，rock strength characteristics and confining stress conditions，as well as the relationships among specific energy，rock strength characteristics and confining stress conditions were obtained. Finally，the entropy weight method was used to evaluate the influence weights of rock strength characteristics and confining stress conditions on the peak indentation force and specific energy. Through the above experimental study，regression analysis，and the weight determination，the necessary theoretical basis can be provided for the feasibility evaluation of non-explosive mechanized mining and the design of rock breaking parameter in deep mine. This study has important guiding significance for the realization of non-explosive mechanized mining in deep hard rock.

Keywords： deep mining ; non-explosive mechanized mining ; rock breakage ; uniaxial confining stress ; rock cuttability ; entropy weight method

PDF (5364KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

唐宇, 王少锋. 单向受限应力下镐型截齿破岩特性及其影响因素分析[J]. 黄金科学技术, 2021, 29(5): 669-679 doi:10.11872/j.issn.1005-2518.2021.05.009

TANG Yu, WANG Shaofeng. Analysis on Rock Breakage Characteristic and Its Influence Factors of Conical Pick Under Uniaxial Confining Stress[J]. Gold Science and Technology, 2021, 29(5): 669-679 doi:10.11872/j.issn.1005-2518.2021.05.009

随着矿山浅部资源开采殆尽，深部开采已是必然趋势。然而，传统的钻爆法已难以适应深部开采对连续化、规模化和安全高效绿色资源开发的需求。基于刀具破岩的非爆机械化开采有望成为深部矿山开采的主要替代方法之一（李夕兵等，2019；王少锋等，2021）。岩石切割是一个复杂的过程，受到众多因素的影响，如切割机械及刀具性能、岩石自身性质和地应力条件等。因此，国内外众多学者开展了大量的机械刀具破岩特性研究。

TBM作为隧道开挖的重要工具，许多学者对其进行了研究。Barton（1999）利用Q系统来评价TBM岩石切割性能。Balci（2009）将试验和现场TBM岩石切割性能相结合，研究了TBM切割性能。Bilgin et al.（2012）和Copur et al.（2014）也通过试验对TBM切割性能进行了研究。与此同时，刀具性能作为提高破岩机械效率的关键因素，引起了众多学者的关注。有学者针对不同刀具对岩石的可切割性影响进行了研究。Chen et al.（2006）采用楔形切割刀具对岩石进行切割试验。Geng et al.（2016）采用圆盘滚刀来研究岩石切割的整个过程。Bilgin et al.（2012）研究了凿刀和圆盘刀具之间的性能差异。Wang et al.（2018，2019）利用镐形截齿在高应力下对岩石进行切割试验，并将其应用于现场机械化开采。Evans（1974）将镐型刀具和圆盘刀具切割效率进行对比分析。然而，在岩石切割过程中，刀具的磨损会严重影响岩石的切割效率。因此如何解决刀具钝化问题，也是提高生产效率的关键。Dogruoz et al.（2010，2014）采用不同钝化程度的刀具对低、微中、中硬度岩石进行切割，并分析了切割性能的影响因素。Rostamsowlat et al.（2018）研究了磨损对刀具切割性能的影响。

此外，岩石性质的差异也会影响岩石切割效率。基于此，McFeat-Smith et al.（1977）通过试验研究了不同岩石性质与切割性能之间的关系。Balci et al.（2012）利用V型切割刀具研究不同岩石的可切割性。Abu Bakar et al.（2014）利用圆盘滚刀分别对干砂岩和饱和砂岩进行了岩石切割性能测试。Yagiz（2008）利用岩体特性预测了TBM的切割性能。

随着开采不断向深部推进，受限应力条件逐渐成为影响岩石切割性的关键因素，甚至当围压过高时，在开采过程中会发生岩爆，严重威胁到人员和设备的安全（冯夏庭等，1998，2012；李夕兵等，2002；何满潮等，2007）。为了解决这一难题，Li et al.（2018）和杜坤（2013）等在不同围压下对岩石进行切割试验；陈景涛等（2006）和龚秋明等（2010）在高地应力下对岩石进行切割试验。同时，大量的数值模拟方法也被应用于破岩机械性能和岩石可切割性研究中（Innaurato et al.，2007；孙金山等，2011；夏毅敏等，2014）。然而，之前的研究鲜有同时考虑地应力条件和不同岩石性质的影响。

为此，本文采用真三轴加载系统，对花岗岩、大理岩、红砂岩和磷矿石进行了不同单向受限应力条件下的岩石切割试验。根据试验结果，构建岩石可切割性与岩石性质和受限应力条件的关系模型，用于科学评价现场矿岩的可切割性，为深部硬岩矿体的非爆机械化开采提供理论与关键技术支撑。

1 试验方法

1.1 试验仪器

本次镐形截齿破岩试验在中南大学开发的真三轴电液伺服诱变（扰动）试验系统上进行。该系统主要由计算机控制系统、液压控制系统和视频成像系统组成。X、Y和Z 3个方向可通过液压柱向岩石施加载荷，来模拟岩石在实际三向、双向和单向边界应力（岩石在立体空间中3个方向上所受到的边界应力情况）下的应力状态，且在X、Y和Z 3个方向上最大加载力分别可达到2 000，2 000，3 000 kN，能够极大程度地模拟岩石在实际现场中所处的应力条件，从而实现不同应力条件下实验室岩石切割测试。

1.2 岩石样本

本次试验采用4类共35组岩石样品，其中花岗岩、大理岩和磷矿石各9组，红砂岩8组，且均为100 mm×100 mm×100 mm的立方体岩样。通过进行单轴抗压强度测试和巴西劈裂试验分别得到4类岩石的单轴抗压强度和抗拉强度，并以试验所得的单轴抗压强度和抗拉强度为基础，计算得到常见的2个与岩石抗压强度和抗拉强度密切相关的脆性指数，其中单轴抗压强度、抗拉强度和脆性指数具体数值如表1所示。脆性指数分为2种（Hucka et al.，1974），分别按照式（1）和式（2）计算得到。

$B_{1} = \frac{σ_{c}}{σ_{t}}$

（1）

$B_{2} = \frac{(σ_{c} - σ_{t})}{(σ_{c} + σ_{t})}$

（2）

式中： $σ_{c}$ 为单轴抗压强度； $σ_{t}$ 为单轴抗拉强度。

表1 岩样力学性质

Table 1 Mechanical properties of rocks

岩石样本	单轴抗压强度 $σ_{c} / M P a$	单轴抗拉强度 $σ_{t} / M P a$	脆性指数 $B_{1}$	脆性指数 $B_{2}$
花岗岩	126.24	7.56	16.698	0.887
大理岩	129.22	6.18	20.909	0.909
红砂岩	97.79	5.31	18.416	0.897
磷矿石	106.21	5.24	20.269	0.906

新窗口打开| 下载CSV

1.3 试验过程

首先，将岩石置于承载台中央。然后，在Y轴的左、右方向，利用液压柱向岩石施加载荷。最后，在安装好截齿的Z轴方向，利用液压柱均匀向岩石施加载荷，直至岩石发生破碎。依次按照上述步骤分别对花岗岩、大理岩、红砂岩和磷矿石进行不同单向受限应力条件下的破岩试验，且单向受限应力的范围选择来源于4类岩石的单轴抗压强度，以不超过其单轴抗压强度为准则，分别在0，5，10，20，40，60，80，100，120 MPa单向受限应力条件下对花岗岩和大理岩进行试验，在0，5，10，20，40，60，80，90 MPa单向受限应力条件下对红砂岩进行试验，在0，5，10，20，40，60，80，90，100 MPa单向受限应力条件下对磷矿石进行试验。

在整个试验过程中，计算机系统会实时记录岩石的载荷变化曲线。根据载荷变化曲线，可得到岩石发生破坏时的破岩峰值载荷和对应的截齿侵入深度。由式（3）计算对应的切割功。通过测量岩石破坏后，截齿所截落的岩块或岩屑体积，由式（4）计算破岩比能。

$W_{c} = \frac{1}{2} F_{c} D_{c}$

（3）

$E_{c} = \frac{W_{c}}{V_{c}}$

（4）

式中： $W_{c}$ 为切割功； $F_{c}$ 为截齿破岩峰值载荷； $D_{c}$ 为截齿侵入深度； $V_{c}$ 为截落体积； $E_{c}$ 为破岩比能。

2 回归分析

为了研究在不同受限应力条件下，岩石自身性质与岩石可切割性之间的关系，结合上述试验结果，将进行归一化处理后的2种脆性指数和单向受限应力作为自变量，建立了一系列与截齿破岩峰值载荷以及破岩比能相关的回归模型，试验获得的35组数据均用于模型建立。其中，模型可划分为无量纲化后的回归模型和没有进行无量纲化处理的一般模型。相较于一般的非无量纲化模型而言，无量纲化后的模型与所选的参量单位无关，使其更具普遍性，消除了各参量不同量纲的影响。最后，利用确定系数R²和均方根误差RMSE对各模型回归效果进行分析和评价，并绘制了试验值与模型预测值之间的对比图，来验证模型回归效果。

2.1 非无量纲化回归模型

以归一化后的脆性指数1和脆性指数2分别为X轴，单向受限应力为Y轴，截齿破岩峰值载荷和破岩比能分别为Z轴，建立了4组回归模型。归一化方程为

$f (x) = \frac{x - x_{m i n}}{x_{m a x} - x_{m i n}}$

（5）

式中：f（x）为归一化后的数值；x为影响因素试验数值；x_min为试验数值的最小值；x_max为试验数值的最大值。

（1）截齿破岩峰值载荷回归模型

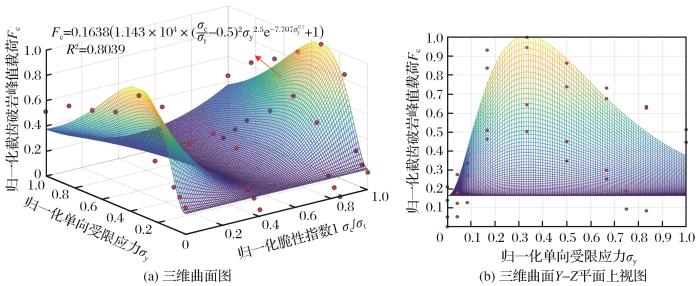
将归一化后的脆性指数1、单向受限应力和截齿破岩峰值载荷分别作为X轴、Y轴和Z轴，通过拟合得到如式（6）所示的回归模型，并绘制如图1所示的回归曲面，其中红色散点是通过归一化处理的试验值。

$\begin{array}{l} F_{c} = 0.1638 [1.143 \times 10^{4} \times \begin{matrix} \end{matrix} \\ {(\frac{σ_{c}}{σ_{t}} - 0.5)}^{2} σ_{y}^{2.5} e^{- 7.707 σ_{y}^{0.7}} + 1] \end{array}$

（6）

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 截齿破岩峰值载荷回归模型（X轴脆性指数1）

Fig.1 Regression model of peak indentation force of pick rock breakage（X-axis brittleness index 1）

以归一化后的脆性指数2、单向受限应力和截齿破岩峰值载荷分别作为X轴、Y轴和Z轴，通过拟合得到如式（7）所示的回归模型，其回归曲面与图1类似。

$\begin{array}{l} F_{c} = 0.1769 {[1 540 \times (\frac{σ_{c} - σ_{t}}{σ_{c} + σ_{t}} - 0.5)}^{4} \\ \begin{matrix} \end{matrix} σ_{y}^{1.5} e^{- 4.248 σ_{y}} + 1] \end{array}$

（7）

（2）破岩比能回归模型

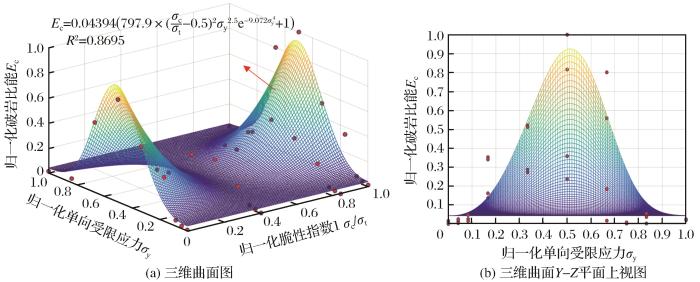
将归一化后的脆性指数1、单向受限应力和破岩比能分别作为X轴、Y轴和Z轴，通过拟合得到如式（8）所示的回归模型，并绘制如图2所示的回归曲面。

$\begin{array}{l} E_{c} = 0.04394 {[797.9 \times (\frac{σ_{c}}{σ_{t}} - 0.5)}^{2} \\ \begin{matrix} \end{matrix} σ_{y}^{2.5} e^{- 9.072 σ_{y}^{4}} + 1] \end{array}$

（8）

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 破岩比能回归模型（X轴脆性指数1）

Fig.2 Regression model of rock breakage specific energy （X-axis brittleness index 1）

将归一化后的脆性指数2、单向受限应力和破岩比能分别作为X轴、Y轴和Z轴，通过拟合得到如式（9）所示的回归模型，其回归曲面与图2类似。

$\begin{array}{l} E_{c} = 0.03315 {[659.6 \times (\frac{σ_{c} - σ_{t}}{σ_{c} + σ_{t}} - 0.5)}^{2} \\ \begin{matrix} \end{matrix} σ_{y}^{2} e^{- 7.792 σ_{y}^{4}} + 1] \end{array}$

（9）

2.2 无量纲化回归模型

首先，对单向受限应力、截齿破岩峰值载荷和破岩比能进行无量纲化处理。将单向受限应力与单轴抗压强度比值、不同受限应力条件下截齿破岩峰值载荷与0 MPa受限应力下峰值载荷比值、不同受限应力条件下的破岩比能与0 MPa受限应力下破岩比能比值，分别作为对应的无量纲值。然后，对其进行归一化处理。最后，进行拟合得到4组回归模型。

（1）截齿破岩峰值载荷回归模型

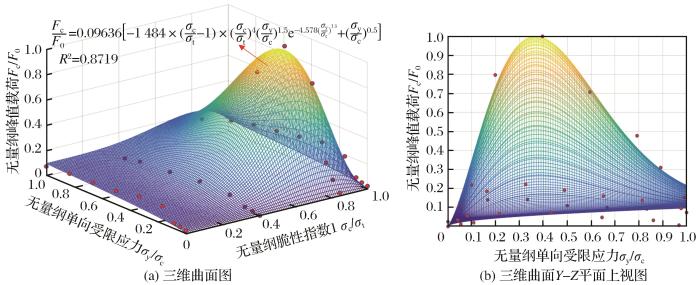
将无量纲化和归一化处理后的脆性指数1、单向受限应力和截齿破岩峰值载荷相关数据分别作为X轴、Y轴和Z轴。通过拟合得到如式（10）所示的回归模型，并根据模型绘制了如图3所示的三维曲面图。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 无量纲化截齿破岩峰值载荷回归模型（X轴脆性指数1）

Fig.3 Dimensionless regression model of peak indentation force of pick rock breakage（X-axis brittleness index 1）

$\frac{F_{c}}{F_{0}} = 0.09636 [- 1 484 \times (\frac{σ_{c}}{σ_{t}} - 1) \times {(\frac{σ_{c}}{σ_{t}})}^{4} {(\frac{σ_{y}}{σ_{c}})}^{1.5} e^{- 4.578 {(\frac{σ_{y}}{σ_{c}})}^{1.5}} + {(\frac{σ_{y}}{σ_{c}})}^{0.5}]$

（10）

针对脆性指数2，通过拟合得到如式（11）所示的回归模型，其三维曲面类似于图3。

$\frac{F_{c}}{F_{0}} = 0.1044 [- 3 293 \times (\frac{σ_{c} - σ_{t}}{σ_{c} + σ_{t}} - 1) \times {(\frac{σ_{c} - σ_{t}}{σ_{c} + σ_{t}})}^{4} \times {(\frac{σ_{y}}{σ_{c}})}^{2} e^{- 5.914 {(\frac{σ_{y}}{σ_{c}})}^{1.5}} + {(\frac{σ_{y}}{σ_{c}})}^{0.5}]$

（11）

（2）无量纲破岩比能回归模型

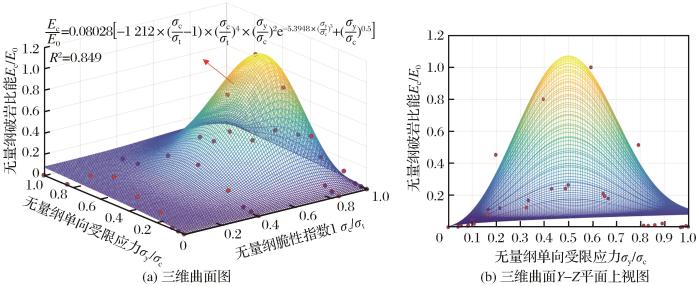
将经过处理的脆性指数1、单向受限应力和破岩比能相关数据分别作为X轴、Y轴和Z轴。通过拟合得到如式（12）所示的回归模型，并根据模型绘制如图4所示的三维曲面图。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 无量纲破岩比能回归模型（X轴脆性指数1）

Fig.4 Dimensionless regression model of rock breakage specific energy （X-axis brittleness index 1）

$\frac{E_{c}}{E_{0}} = 0.08028 [- 1 212 \times (\frac{σ_{c}}{σ_{t}} - 1) \times {(\frac{σ_{c}}{σ_{t}})}^{4} \times {(\frac{σ_{y}}{σ_{c}})}^{2} e^{- 5.3948 {(\frac{σ_{y}}{σ_{c}})}^{3}} + {(\frac{σ_{y}}{σ_{c}})}^{0.5}]$

（12）

针对脆性指数2，通过拟合得到如式（13）所示的回归模型，其三维曲面类似于图4。

$\frac{E_{c}}{E_{0}} = 0.07237 [- 2 895 \times (\frac{σ_{c} - σ_{t}}{σ_{c} + σ_{t}} - 1) \times {(\frac{σ_{c} - σ_{t}}{σ_{c} + σ_{t}})}^{4} \times {(\frac{σ_{y}}{σ_{c}})}^{2.5} e^{- 5.916 {(\frac{σ_{y}}{σ_{c}})}^{2.5}} + {(\frac{σ_{y}}{σ_{c}})}^{0.5}]$

（13）

2.3 模型评价

利用确定性系数 $R^{2}$ 和均方差误差 $R M S E$ 对所建立的回归模型进行分析和评价。由式（14）和式（15）计算得各模型的 $R^{2}$ 和 $R M S E$ 值，列于表2中。

$R^{2} = \sum_{i = 1}^{n} (y_{p (i)} {- \bar{y_{t}})}^{2} / \sum_{i = 1}^{n} (y_{t (i)} {- \bar{y_{t}})}^{2}$

（14）

RMSE=

$\sqrt[]{\frac{1}{n} \sum_{i = 1}^{n} (y_{t (i)} - y_{p (i)})^{2}}$

（15）

式中： $n$ 为样本数量； $y_{p (i)}$ 为回归预测值； $y_{t (i)}$ 为试验测试值； $\bar{y_{t}}$ 为试验测试值的平均值。

表2 回归模型R²和RMSE值

Table 2 R²and RMSE of regression models

评价指标	非无量纲化回归模型				无量纲化回归模型
	脆性指数1		脆性指数2		脆性指数1		脆性指数2
	F_c/kN	E_c/（10^-3J·cm^-3）	F_c/kN	E_c/（10^-3J·cm^-3）	F_c/F₀	E_c/E₀	F_c/F₀	E_c/E₀
$R^{2}$	0.8039	0.8695	0.7845	0.8573	0.8719	0.8490	0.8110	0.8235
$R M S E$	27.14	924.69	28.46	966.98	2.17	19.37	2.64	32.29

新窗口打开| 下载CSV

然后，根据得到的模型，将各原始参数代入回归模型，得到初始预测值，再通过反归一化得到最终的预测值。图5和图6分别为非无量纲和无量纲下截齿破岩峰值载荷和破岩比能的预测值和试验值对应分布图。

图5

新窗口打开| 下载原图ZIP| 生成PPT

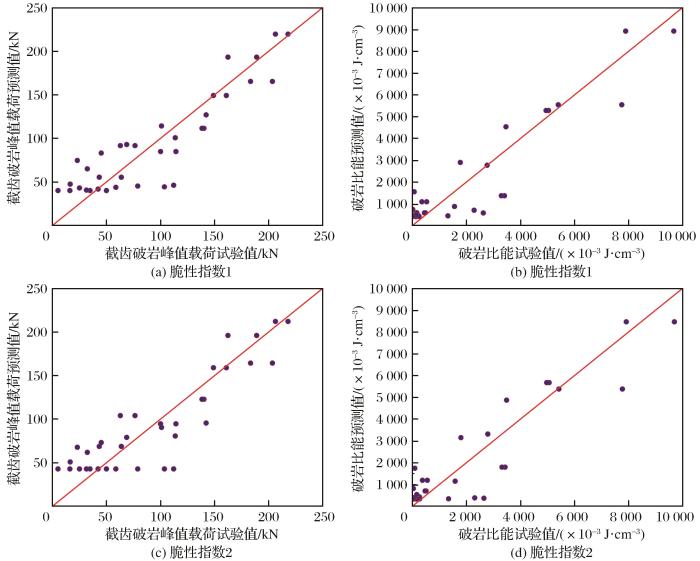
图5 非无量纲回归模型预测值与试验值对比

Fig.5 Comparison of predicted and experimental values of non-dimensionless regression model

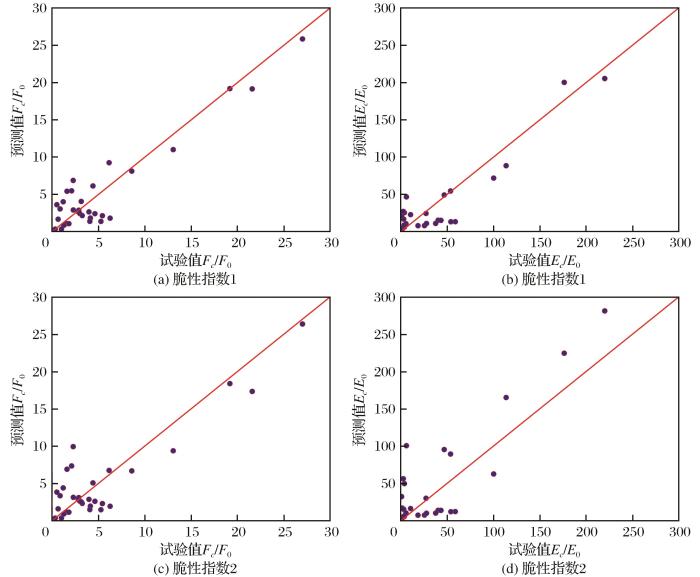
图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 无量纲回归模型预测值与试验值对比

Fig.6 Comparison of predicted and experimental values of dimensionless regression model

2.4 脆性指数和受限应力条件对破岩特性的影响分析

（1）脆性指数影响。通过回归分析可得，无论是在非无量纲还是无量纲条件下的回归模型，单向受限应力和两类脆性指数对截齿破岩峰值载荷和破岩比能的影响均呈非线性变化，且在不同脆性指数范围内，对岩石的可切割性影响不同。其中，对于非无量纲回归模型，将其脆性指数1划分为2个区间：区间1为16.698~18.416，区间2为18.417~20.909。在区间1内，截齿破岩峰值载荷和破岩比能随着脆性指数1的增加而减少，即岩石的可切割性增加；而在区间2内，截齿破岩峰值载荷和破岩比能随着脆性指数1的增加而增加，即岩石的可切割性降低。同样，脆性指数2也可以划分为2个区间：区间1为0.887~0.897，区间2为0.898~0.909。与脆性指数1类似，在区间1内，截齿破岩峰值载荷和破岩比能随着脆性指数2的增加而减少，岩石的可切割性增加；而在区间2内，截齿破岩峰值载荷和破岩比能随着脆性指数2的增加而增加，岩石的可切割性降低。

对于无量纲回归模型，当脆性指数1在16.698~20.269范围内，脆性指数2在0.887~0.906范围内时， $F_{c} / F_{0}$ 和 $E_{c} / E_{0}$ 均随着脆性指数的增加而增加；当脆性指数1在20.270~20.907范围内，脆性指数2在0.907~0.909范围内时， $F_{c} / F_{0}$ 和 $E_{c} / E_{0}$ 均随着脆性指数的增加而减少。

（2）受限应力条件影响。随着单向受限应力的增加，所有的截齿破岩峰值载荷和破岩比能均呈现出先增加后减少的趋势，意味着岩石的可切割性随着单向受限应力的增加先减少后增加。试验结果和回归分析表明，单向受限应力对岩石可切割性的影响可划分为3个区域：区域1，当单向受限应力小于岩石单轴抗压强度的30%~40%时，单向受限应力的增大对岩石可切割性起阻碍作用；区域2，当单向受限应力小于岩石单轴抗压强度的40%~80%时，单向受限应力的继续增大反而对岩石可切割性有一定的促进作用；区域3，当单向受限应力达到岩石单轴抗压强度的80%以上时，纵使单向受限应力对岩石的可切割性继续起促进作用，但在较高的单向受限应力条件下，由于岩石切割的点载荷扰动作用，会引发岩爆现象。

3 熵权法权重评价

熵权法是利用指标变异性大小来确定客观权重的方法，其广泛应用于工程技术和社会经济等领域。本文以上述模型为基础，借用熵权法来评价岩石自身性质和受限应力条件对岩石可切割性的影响权重。熵权法确定指标权重步骤如下：

（1）数据标准化。在采用熵权法之前，需要对每个数据进行归一化处理。但根据指标性质的不同采用的归一化处理方式也不同，本文采用式（16）对数据进行归一化。

$Y_{i j} = \frac{X_{i j} - m i n (X_{i})}{m a x (X_{i}) - m i n (X_{i})}$

（16）

（2）求指标信息熵。信息熵E_j反映了指标变异程度的大小。E_j越小，表明变异程度越大，能够提供的信息量越大，在指标衡量中的作用也越大，则权重也越大，反之则权重越小。信息熵E_j的计算公式为

$E_{j} = - K \sum_{i = 1}^{n} P_{i j} l n P_{i j}$

（17）

式中： $E_{j}$ 为第 $j$ 个指标的信息熵；K为熵系数， $K = l n {(n)}^{- 1}$ ；n为该指标的样本总数； $P_{i j} = \frac{Y_{i j}}{\sum_{i = 1}^{n} Y_{i j}}$ 。

（3）权重计算。结合步骤（2）计算得到的信息熵，计算各指标权重，表示为

$W_{j} = \frac{(1 - E_{j})}{(m - \sum_{j = 1}^{m} E_{j})}$

（18）

式中：W_j为指标权重；m为信息熵总个数。

按照上述步骤，对不同脆性指数下无量纲化和非无量纲化下的岩石自身性质及受限应力条件进行了权重评价，通过计算得到脆性指数1、脆性指数2的指标信息熵分别为0.9003和0.9038，无量纲单向受限应力和没有进行无量纲化处理的单向受限应力的信息熵分别为0.8825和0.8834。计算所得的最终权重值见表3。

表3 岩石性质和单向受限应力权重值

Table 3 Weight values of rock properties and uniaxial confining pressure

影响权重	非无量纲回归模型		无量纲回归模型
影响权重	脆性指数1	脆性指数2	脆性指数1	脆性指数2
岩石性质	0.459	0.450	0.461	0.452
受限应力条件	0.541	0.550	0.539	0.548

新窗口打开| 下载CSV

结果表明，无论利用脆性指数1还是脆性指数2，无量纲化或非无量纲化下的单向受限应力权重总是大于岩石自身性质权重。所以，岩石在切割过程中所受到的受限应力条件比岩石自身性质对岩石可切割性的影响更大。但是，由于权重值差别不大，因此，岩石性质和受限应力条件对岩石的可切割性均具有重要影响。

4 结论

通过开展不同受限应力条件下花岗岩、大理岩、红砂岩和磷矿石的截齿破岩试验，研究不同单向受限应力和不同岩石性质对岩石可切割性的影响。然后，基于试验所得数据建立了脆性指数、单向受限应力与截齿破岩峰值载荷及破岩比能之间的归一化回归模型，其中包括非无量纲和无量纲两类归一化回归模型。最后，采用熵权法衡量了岩石性质和受限应力条件对岩石可切割性的影响权重，得到如下结论：

（1）所建立的回归模型能够较好地反映岩石脆性指数、单向受限应力与岩石可切割性之间的关系。对于非无量纲模型，截齿破岩峰值载荷和破岩比能随着脆性指数的增加先降低后升高，岩石可切割性先增加后减少；对于无量纲模型，随着脆性指数的增加，截齿破岩峰值载荷和破岩比能先升高后降低，岩石的可切割性先减少后增加。然而，就单向受限应力对岩石可切割性的影响而言，无论是非无量纲模型还是无量纲模型，岩石的可切割性均随着单向受限应力的增加先减少后增加。

（2）通过熵权法分析了岩石脆性指数和单向受限应力对岩石可切割性的影响权重，结果表明，受限应力条件对岩石可切割性的影响大于岩石脆性指数，但是由于权重值差别不大，因此，岩石性质和受限应力条件均被视为影响岩石可切割性的重要因素。

（3）本文构建的考虑岩石性质和受限应力条件的岩石可切割性定量模型有望应用到采矿实际过程中，通过现场矿岩的力学性质和应力条件来评价矿岩的可切割性，从而为合理设计深部矿山非爆机械化开采技术参数提供理论依据。

http://www.goldsci.ac.cn/article/2021/1005-2518/1005-2518-2021-29-5-669.shtml

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[]

Abu Bakar

M Z

，Gertsch

L S

，Rostami

，2014.

Evaluation of fragments from disc cutting of dry and saturated sandstone

［J］.Rock Mechanics and Rock Engineering，47：1891-1903.

Balci

，2009.

Correlation of rock cutting tests with field performance of a TBM in a highly fractured rock formation： A case study in Kozyatagi-Kadikoy metro tunnel，Turkey

［J］.Tunnelling & Underground Space Technology， 24：423-435.DOI：https：//doi.org/10.1016/j.tust.2008.12.001.