基于正态隶属度—属性区间识别模型的岩爆倾向等级预测

doi:10.11872/j.issn.1005-2518.2022.03.037

基于正态隶属度—属性区间识别模型的岩爆倾向等级预测

贡力^,¹^,², 陆丽丽^,¹, 靳春玲¹, 梁栋³, 周汉国³, 谢平³

1.兰州交通大学土木工程学院，甘肃兰州 730070

2.兰州交通大学调水工程及输水安全研究所，甘肃兰州 730070

3.中国中铁科学研究院有限公司，四川成都 610000

Propensity Grade Prediction of Rockburst Based on Normal Membership-Attribute Interval Recognition Model

GONG Li^,¹^,², LU Lili^,¹, JIN Chunling¹, LIANG Dong³, ZHOU Hanguo³, XIE Ping³

1.College of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, Gansu, China

2.Institute of Water Diversion Engineering and Water Security, Lanzhou Jiaotong University, Lanzhou 730070, Gansu, China

3.China Railway Academy Co. , Ltd. , Chengdu 610000, Sichuan, China

通讯作者: 陆丽丽（1994-），女，甘肃白银人，硕士研究生，从事土木工程建造与管理方面的研究工作。lullin@qq.com

收稿日期: 2021-03-05 修回日期: 2021-08-29

基金资助:

国家自然科学基金项目“西北盐渍干寒地区多因素耦合作用下长距离明渠的劣化机理研究”. 51969011
甘肃省科技计划资助项目“ 黄河流域突发水污染应急调控关键技术与应用”. 20JR10RA274

Received: 2021-03-05 Revised: 2021-08-29

作者简介 About authors

贡力（1977-），男，江苏丹阳人，教授，博士生导师，从事深埋隧道及输水工程方面的研究工作gongl@mail.lzjtu.cn , E-mail：gongl@mail.lzjtu.cn

摘要

岩爆是地下工程开挖面临的关键问题之一，为了准确预测深埋隧洞中岩爆烈度倾向等级，提出了正态隶属度—属性区间识别模型的岩爆预测方法。针对岩爆倾向等级属于典型的多属性有序分割类问题，构建了属性区间识别模型，并将岩爆倾向等级划分为4个等级进行预测。根据岩爆发生的成因和机理，选取应力系数、脆性系数、弹性应变指数和岩石完整性系数作为预测指标，考虑各指标之间、指标与标准等级之间的交互关系，采用正态隶属度函数和Jousselme距离计算评价指标权重。结合13个深埋隧洞工程对该预测模型进行准确性测试，并以双江口水电站SPD9厂房为例进行工程实例验证，该模型预测结果与实际相吻合，证明该模型用于具体工程实践中是可行且有效的，研究结果可为类似深埋隧洞岩爆倾向等级预测提供新的思路。

关键词： 深埋隧洞 ; 岩爆倾向等级 ; 岩爆预测 ; 正态隶属度函数 ; 属性区间识别模型 ; 均化系数

Abstract

Rockburst is one of the key problems in underground engineering excavation，in order to accurately predict the grade of rockburst propensity in deep-buried tunnels，a rockburst prediction method based on the normal membership degree-attribute interval recognition model was proposed.Due to the rockburst propensity is a typical multi-attribute orderly segmentation problem，the attribute interval recognition model was constructed to divide the rockburst propensity into four grades for prediction.The occurrence of rockburst is affected by engineering geology，and the geological parameter is usually an interval value.The attribute interval recognition model can be better applied to the problem that each grade index value is an interval value.According to the mechanism of rockburst，the stress coefficient，brittleness coefficient，elastic strain index and rock integrity coefficient were selected as predictive indicators，considering the interaction between the indicators and the standard grade，the normal membership function and Jousselme distance were used to calculate the weight of the index.The method had different weights for the measured values of different indexes under the same index system，which can avoid the drawback that the traditional method didn’t consider the interaction relationship between the indexes，and improve the robustness of the model.The accuracy of the prediction model was tested with 13 deep-buried tunnel projects.Since the value of the averaging coefficient had a greater impact on the prediction accuracy of the model，in order to obtain the optimal value of the averaging coefficient，the step size was 0.1 and selected within the interval ［0.05，0.95］.The analysis shows that when the averaging coefficient is 0.65，the prediction accuracy of the model is the highest，which is 92.31%.The left bank of SPD9 in the Huangjiangkou hydropower project was used to verify the model.The prediction results are consistent with the actual rockburst propensity grade.The prediction results prove that the model is feasible and effective in specific engineering practice，and it can provide new ideas for predicting the rockburst propensity grade in similar deep-buried tunnels.

Keywords： deep-buried tunnels ; rockburst propensity grade ; rockburst prediction ; normal membership function ; attribute interval recognition model ; averaging coefficient

PDF (1004KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

贡力, 陆丽丽, 靳春玲, 梁栋, 周汉国, 谢平. 基于正态隶属度—属性区间识别模型的岩爆倾向等级预测[J]. 黄金科学技术, 2022, 30(3): 404-413 doi:10.11872/j.issn.1005-2518.2022.03.037

GONG Li, LU Lili, JIN Chunling, LIANG Dong, ZHOU Hanguo, XIE Ping. Propensity Grade Prediction of Rockburst Based on Normal Membership-Attribute Interval Recognition Model[J]. Gold Science and Technology, 2022, 30(3): 404-413 doi:10.11872/j.issn.1005-2518.2022.03.037

岩爆是一种发生在深埋隧洞中的常见地质灾害，是隧洞开挖工程中由于岩体本身积聚的应变能量超过岩体破坏时消耗的能量，岩石受到应力重分布作用将多余能量释放出来致使岩石发生爆裂、剥离的现象（李任豪等，2020）。岩爆是高地应力地区常见的地质现象，最早发生在矿井中，后来随着大量深埋隧洞修建于高地应力区域，岩爆问题受到了矿山和隧道工程领域研究人员的重视。为了降低岩爆灾害对作业人员及机械的损害程度，探寻科学、合理的岩爆倾向等级预测方法对岩爆防控具有极其重要的意义。

多年来，众多学者对岩爆预测展开了诸多研究。早期岩爆预测研究只考虑单一因素的影响，如：岩石刚度、强度和能量等，且国内外学者提出了不同的判据，如：Russense判据（张镜剑等，2008）和Kidybinski判据（Kidybinski，1981）等。然而，岩爆发生受多种因素共同制约，单一判据具有片面性。随着岩爆灾害研究工作的深入，岩爆发生的影响因素与岩爆倾向等级的非线性关系逐渐引起学者们的关注，新的数学方法及智能算法模型开始应用到岩爆预测过程中。数学方法主要有模糊综合评判法（Adoko et al.，2013；王元汉等，1998）、物元可拓理论（张乐文等，2010）、灰色系统理论（裴启涛等，2013）、功效系数法（王迎超等，2014）和云模型（王迎超等，2015）等。智能算法主要有BP神经网络（孙臣生，2019）、人工神经网络（张光存等，2013）、深度神经网络（田睿等，2020）和随机森林方法（Dong et al.，2013）等。

上述方法在岩爆倾向等级预测方面取得了一定的成果，但是由于岩爆预测的复杂性，这些方法在实际应用中仍存在2个问题：（1）各种方法自身具有一定的局限性，例如：模糊综合评价法在确定指标权重时，人为因素的影响较多，评判结果不够客观；BP神经网络学习速率的选择缺乏有效的方法且不能保证收敛到全局最小点；随机森林法对于小样本数据可信度不高。（2）运用非线性关系评价方法的核心是指标权重的计算，其中应用较广的是采用主观权重与客观权重相结合来消除单一权重的影响，但其核心是针对评价指标体系的构建，忽略了指标实测值的改变以及其余指标对权重的影响，导致同一指标体系下的不同工程实例和不同指标实测值所赋权重均相同。

岩爆倾向等级预测属于多属性有序分割类问题，通过分析现有数学方法和智能算法，发现智能算法应用简单，计算过程全部由软件驱动，但是部分智能算法由于初始化随机权重使得计算结果不稳定。而数学方法可以避免该缺点，其中属性区间识别模型在解决多属性有序分割类问题上具有明显的优越性（殷欣等，2020）。因此，本文引入属性区间识别模型进行岩爆倾向等级预测。为了避免权重计算出现前述问题，本文采用正态隶属度函数计算指标概率密度，并利用Jousselme公式计算指标间距离，进而确定指标权重。该方法从各指标所属各等级的距离出发，综合考虑各指标各等级间的相互影响程度，对同一指标体系下不同工程实例赋予不同权重值，使得权重计算相对更加合理。最后，应用13个典型深埋引水隧洞案例进行模型准确性测试，并以双江口水电站SPD9厂房为例进行了工程实例验证，结果表明该模型预测结果能够客观反映岩爆实际结果，可为预测类似深埋引水隧洞岩爆倾向等级提供新思路。

1 属性区间识别模型

设D为全体待评价隧洞，D_i ∈D（i=1，2，…，m）为若干典型的待评价隧洞，每个隧洞有n个评价指标I₁，I₂，…，I_n，x_ij 为第i个标段的第j个评价指标的测量值。假定G为D上的某类属性空间，评价集（E₁，E₂，…，E_k ）为属性测度区间空间G的有序分割类，根据已知的分级标准构造标准的分级矩阵为

[\begin{matrix} E_{1} & E_{2} & \dots & E_{k} \\ I_{1} & [a_{11}, b_{11}] & [a_{12}, b_{12}] & \dots & [a_{1 k}, b_{1 k}] \\ I_{2} & [a_{21}, b_{21}] & [a_{22}, b_{22}] & \dots & [a_{2 k}, b_{2 k}] \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ I_{n} & [a_{n 1}, b_{n 1}] & [a_{n 2}, b_{n 2}] & \dots & [a_{n k}, b_{n k}] \end{matrix}]

（1）

式中： $a_{j p}, b_{j p}$ （1 $\leq j \leq n, 1 \leq p \leq k)$ 为第j个评价指标在评价集E_p 上的端点值，且满足 $a_{j 1} < a_{j 2} < \dots < a_{j k}, b_{j 1} < b_{j 2} < \dots < b_{j k}$ 或者 $a_{j 1} > a_{j 2} > \dots > a_{j k}, b_{j 1} > b_{j 2} > \dots > b_{j k}$ 。

1.1 单指标属性测度区间的计算

将x_ij 具有属性E_p （1≤p≤k）的属性测度区间记为 $[μ_{i j p}] = [{\underset{̲}{μ}}_{i j p}, {\bar{μ}}_{i j p}]$ ，则有：

当

x_{i j} \leq a_{j 1} (x_{i j} \geq a_{j 1}

）时，有

{\underset{̲}{μ}}_{i j 1} = 1, {\underset{̲}{μ}}_{i j 2}

\dots = {\underset{̲}{μ}}_{i j k}

=0；（2）

当

x_{i j} \leq b_{j 1} (x_{i j} \geq b_{j 1}

）时，有

{\bar{μ}}_{i j 1} = 1, {\bar{μ}}_{i j 2}

\dots = {\bar{μ}}_{i j k}

=0；（3）

当

x_{i j} \geq a_{j k} (x_{i j} \leq a_{j k}

）时，有

{\underset{̲}{μ}}_{i j k} = 1, {\underset{̲}{μ}}_{i j 1}

\dots = {\underset{̲}{μ}}_{i j (k - 1)}

=0；（4）

当

x_{i j} \geq b_{j k} (x_{i j} \leq b_{j k}

）时，有

{\bar{μ}}_{i j k} = 1, {\bar{μ}}_{i j 1}

\dots = {\bar{μ}}_{i j (k - 1)}

=0；（5）

当 $a_{j y} \leq x_{i j} \leq a_{j (y + 1)}$ （ $a_{j (y + 1)} \leq x_{i j} \leq a_{j y}$ ）（1 $\leq$ y $\leq$ k-1）时，则有：

\{\begin{matrix} {\underset{̲}{μ}}_{i j y} = \frac{|x_{i j} - a_{j (y + 1)}|}{|a_{j y} - a_{j (y + 1)}|} \\ {\underset{̲}{μ}}_{i j p} = 0 (p < y 或 p > y + 1) \\ {\underset{̲}{μ}}_{i j (y + 1)} = \frac{|x_{i j} - a_{j y}|}{|a_{j y} - a_{j (y + 1)}|} \end{matrix}

（6）

当 $b_{j y} \leq x_{i j} \leq b_{j (y + 1)}$ （ $b_{j (y + 1)} \leq x_{i j} \leq b_{j y}$ ）（1 $\leq$ y $\leq$ k-1）时，则有：

\{\begin{matrix} {\bar{μ}}_{i j y} = \frac{|x_{i j} - b_{j (y + 1)}|}{|b_{j y} - b_{j (y + 1)}|} \\ {\bar{μ}}_{i j p} = 0 (p < y 或 p > y + 1) \\ {\bar{μ}}_{i j (y + 1)} = \frac{|x_{i j} - b_{j y}|}{|b_{j y} - b_{j (y + 1)}|} \end{matrix}

（7）

1.2 综合属性测度的计算

将均化系数（邹强等，2011）引入属性测度区间，计算各指标的综合属性测度 $μ_{i j p}$ ，表示为

μ_{i j p} = ε {\underset{̲}{μ}}_{i j p} + (1 - ε) {\bar{μ}}_{i j p}

（8）

式中：ε为均化系数，ε∈（0，1）。

1.3 待评价隧洞等级识别

通过综合属性测度计算第i个评价标段属于等级E_p 的综合属性测度μ_ip，表示为

μ_{i p} = \sum_{j = 1}^{n} w_{j} μ_{i j p} (1 \leq i \leq m, 1 \leq p \leq k)

（9）

式中：w_j 为第j个评价指标的权重。

按照置信度准则，取置信度λ（0.5≤λ≤1），若p满足式（10），则可确定评价对象x_i 属于第p个评价等级E_p。

p_{i} = m i n \{p : \sum_{y = 1}^{p} μ_{i y} \geq λ, 1 \leq p \leq k\}

（10）

2 权重的确定

2.1 正态隶属度函数

评价对象的性质决定评价指标，模糊理论的关键是建立指标隶属度函数（林大涌等，2018）。正态隶属度函数具有模糊性，且能够减少主观因素的影响，因此本文采用正态隶属度函数来确定岩爆评价指标属于某评价等级的隶属度，具体公式如下：

u (x) = e^{- {[(x - \bar{x}) / c]}^{2}}

（11）

c = \frac{a_{k}^{+} - a_{k}^{-}}{2 \sqrt[]{- l n (0.5)}}

（12）

式中： $x$ 为指标的实测值； $\bar{x}$ 为某等级区间的均值； $a_{k}^{+}$ 和 $a_{k}^{-}$ 为评价等级的端点值。

各评价等级指标边界值与相邻2个评价等级隶属度相同，因此计算某评价等级端点值时，式（11）中的c应为2c。假设各评价等级 $k$ 用 $a_{k}^{-}, {\bar{a}}_{k}, a_{k}^{+}$ 表示，其中， ${\bar{a}}_{k}$ 表示该等级区间的均值， $a_{k}^{-}$ 和 $a_{k}^{+}$ 表示该等级区间的上限值和下限值， $x$ 为岩爆某指标的实测值。用任意区间k对应岩爆评价等级中的非边界评价等级，则以k=1对应第一个评级等级，k+1对应最后一个评价等级，将正态隶属度函数推广到一般形式，可得到各区间的一般表达式（以效益型指标为例）：

u_{k + 1} (x) = \{\begin{array}{l} 1 (x < {\bar{a}}_{k + 1}) \\ e^{- {[\sqrt[]{- l n (0.5)} (\frac{x - {\bar{a}}_{k + 1}}{a_{k + 1}^{+} - {\bar{a}}_{k + 1}})]}^{2}} ({\bar{a}}_{k + 1} \leq x \leq a_{k + 1}^{+}) \\ 1 - e^{- {[\sqrt[]{- l n (0.5)} (\frac{x - {\bar{a}}_{k}}{{\bar{a}}_{k} - a_{k + 1}^{+}})]}^{2}} (a_{k + 1}^{+} \leq x \leq {\bar{a}}_{k}) \end{array}

（13）

u_{k} (x) = \{\begin{array}{l} 0 (x \leq {\bar{a}}_{k + 1}, x \geq {\bar{a}}_{k - 1}) \\ 1 - e^{- {[\sqrt[]{- l n (0.5)} (\frac{x - {\bar{a}}_{k + 1}}{{\bar{a}}_{k} - {\bar{a}}_{k + 1}})]}^{2}} ({\bar{a}}_{k + 1} < x \leq a_{k}^{-}) \\ e^{- {[2 \sqrt[]{- l n (0.5)} (\frac{x - {\bar{a}}_{k}}{a_{k}^{+} - a_{k}^{-}})]}^{2}} (a_{k}^{-} \leq x < a_{k}^{+}) \\ 1 - e^{- {[\sqrt[]{- l n (0.5)} (\frac{x - {\bar{a}}_{k - 1}}{{\bar{a}}_{k - 1} - a_{k}^{+}})]}^{2}} (a_{k}^{-} \leq x < a_{k}^{+}) \end{array}

（14）

u_{1} (x) = \{\begin{array}{l} 0 (x \leq {\bar{a}}_{k}) \\ 1 - e^{- {[\sqrt[]{- l n (0.5)} (\frac{x - {\bar{a}}_{k}}{a_{1}^{-} - {\bar{a}}_{k}})]}^{2}} ({\bar{a}}_{1} < x \leq a_{1}^{-}) \\ e^{- {[\sqrt[]{- l n (0.5)} (\frac{x - {\bar{a}}_{1}}{a_{1}^{-} - {\bar{a}}_{1}})]}^{2}} (a_{1}^{-} < x \leq {\bar{a}}_{1}) \\ 1 (x > {\bar{a}}_{1}) \end{array}

（15）

根据式（13）~式（15）确定各评价指标对应各评价等级的隶属度函数。

2.2 指标权重的确定

评价指标的权重值是度量指标重要性的方法。考虑各指标间以及各等级间的相互影响，采用指标间的相互距离计算指标权重。正态隶属度函数确定的指标隶属度又称为指标概率密度，由概率密度计算指标距离进而确定权重，计算步骤如下：

设I_i 和I_j 为指标集合中的2个评价指标，则其对应的各等级概率密度为m_i 和m_j，计算指标I_i 和I_j 之间的Jousselme距离d_ij （Shen et al.，2019），表示为

d_{i j} = \sqrt[]{0.5 ({‖m_{i}‖}^{2} + {‖m_{j}‖}^{2} - 2 〈m_{i}, m_{j}〉)}

（16）

式中：m_i 和m_j $为对应的各等级概率密度; 〈m_{i}, m_{j}〉$ 为2个向量内积。

由指标间的距离可以计算指标I_i 和I_j 的信任度，表示为

α_{i j} = 1 - d_{i j} (i, j = 1,2, \dots, n)

（17）

指标I_i 相对于指标I_j 的可信度为

s u p (M_{i}) = \sum_{j = 1, j \neq i}^{n} α_{i j} (i = 1,2, \dots, n)

（18）

将各指标的可信度进行归一化处理，得到指标权重，表示为

w_{i} = \frac{s u p (M_{i})}{\sum_{i = 1}^{n} s u p (M_{i})} (i = 1,2, \dots, n)

（19）

3 模型验证

3.1 构建岩爆倾向等级评价指标体系

内因和外因共同作用造成岩爆灾害。其中，内因是指岩石的物理力学性质，外因是指不同的开挖方式造成岩石应力重分布。目前，关于岩爆等级评价指标的选择国内外没有统一的理论标准，因此本文在参考大量岩爆实例和已有岩爆判据（Wang et al.，2020；Russenes，1974）的基础上，选择4个评价指标：（1）应力系数，即岩石最大切向应力与单轴抗压强度之比σ_θ/σ_c，比值大小代表岩体的强度条件，而岩爆灾害多发生于硬岩条件下；（2）脆性系数，即岩石单轴抗压强度与抗拉强度之比σ_c/σ_t，比值大小代表岩体的稳定性条件，稳定性越差则岩爆程度越严重；（3）弹性应变指数W_et，反映了岩石储存弹性变形势能的能力，数值越大则发生岩爆灾害的倾向性越大；（4）岩石完整性系数k_v，岩石完整性越好，越容易储存应变能量，发生岩爆灾害的倾向性也越大。

以上评价指标相互独立又相互关联，参照王元汉等（1998）、殷欣等（2020）和刘晓悦等（2021）的研究，将岩爆等级划分为4个区间，即：无岩爆（Ⅰ级）、弱岩爆（Ⅱ级）、中等岩爆（Ⅲ级）和剧烈岩爆（Ⅳ级），并确定了岩爆等级与评价指标之间的关系，如式（20）所示。由式（20）可以看出，每个评价指标集的端点值均满足 $a_{j 1} < a_{j 2} < \dots < a_{j k}, b_{j 1} < b_{j 2} < \dots < b_{j k}$ ，因此可以判定岩爆倾向等级预测属于典型的有序分割类问题。

[\begin{matrix} Ⅰ & Ⅱ & Ⅲ & Ⅳ \\ σ_{θ} / σ_{θ} & [0.1,0.3] & [0.3,0.5] & [0.5,0.7] & [0.7,0.9] \\ σ_{o} / σ_{t} & [40.0,46.0] & [26.7,40.0] & [14.5,26.7] & [0.0,14.5] \\ W_{e t} & [0.0,2.0] & [2.0,3.5] & [3.5,5.0] & [5.0,6.5] \\ k_{v} & [0.0,0.55] & [0.55,0.65] & [0.65,0.75] & [0.75,1.0] \end{matrix}]

（20）

在工程实践中常采用微震监测法和声发射监测法进行岩爆监测，岩爆等级的特征描述如表1所示。

表1 岩爆倾向等级的特征描述

Table 1 Characteristic description of rockburst tendency grade

岩爆倾向等级	分级特征描述
无岩爆（Ⅰ级）	表层围岩没有出现爆炸脱落、剥离等现象，对施工基本无影响
弱岩爆（Ⅱ级）	表层围岩出现爆裂脱落、剥离等现象，并且内部不时出现轻微噼啪、撕裂声，对施工影响较小
中等岩爆（Ⅲ级）	围岩爆裂脱落、剥离现象较严重，出现少量弹射、偶尔抛射现象，时常发出尖锐爆裂声音，破坏范围明显，对施工有一定影响
强岩爆（Ⅳ级）	围岩大片爆裂脱落，出现强烈弹射现象，持续发出尖锐爆裂声音，围岩急剧变形，严重影响施工

新窗口打开| 下载CSV

3.2 深埋隧洞工程数据

为了验证本文所用模型的准确性，选取国内外13个典型深埋隧洞原始数据进行数据处理，指标实测值见表2。

表2 典型深埋隧洞原始数据

Table 2 Original index of typical deep-buried tunnels

深埋隧洞编号	工程名称	评价指标实测值				文献来源
深埋隧洞编号	工程名称	σ_θ/σ_c	σ_c/σ_t	W_et	k_v	文献来源
1	天生桥二级水电站引水隧洞	0.30	24.0	6.60	0.73	陈祥等（2009）、张彪等（2017）
2	瀑布沟地下水电站地下洞室	0.33	24.6	5.00	0.80	徐琛等（2017）
3	二滩水电站2#支洞	0.41	29.7	7.30	0.64	殷欣等（2020）、张彪等（2017）
4	鲁布革水电站引水隧洞	0.23	27.8	7.80	0.69	陈祥等（2009）、张彪等（2017）
5	李家峡水电站地下洞室	0.10	23.0	5.70	0.34	张研等（2011）、殷欣等（2020）
6	鱼子溪水电站引水隧洞	0.53	14.8	9.00	0.71	陈祥等（2009）、张彪等（2017）
7	Vietas水电站引水隧洞	0.44	26.7	5.50	0.73	殷欣等（2020）
8	太平驿水电站引水隧洞	0.38	17.6	9.00	0.75	陈祥等（2009）、张研等（2011）
9	锦屏一级水电站引水隧洞	0.67	12.0	3.50	0.53	徐琛等（2017）
10	猴子岩水电站引水隧洞	0.54	28.5	4.71	0.55	贾哲强等（2016）
11	锦屏二级水电站引水隧洞	0.82	18.5	3.80	0.80	陈祥等（2009）、张彪等（2017）
12	龙羊峡水电站地下洞室	0.11	31.2	7.40	0.42	刘冉等（2019）、殷欣等（2020）
13	挪威Sima水电站地下厂房	0.27	21.7	5.00	0.81	李鹏程等（2019）

新窗口打开| 下载CSV

3.3 指标权重的确定

采用正态隶属度函数计算各指标的基本概率分配值，利用Jousselme距离计算指标间距离，然后通过指标间距离值确定指标的信任度，最后通过指标信任度计算每个指标的权重，具体计算过程如下：

（1）根据表2和式（20），利用式（13）~式（15）的指标隶属度函数计算各指标基本概率分配值。以天生桥二级水电站引水隧洞为例，计算结果列于表3中。

表3 指标概率分配表

Table 3 Probability assignment of each index

评价指标	岩爆倾向等级基本概率分配
评价指标	Ⅰ级	Ⅱ级	Ⅲ级	Ⅳ级
σ_θ/σ_c	0.5000	0.5000	0.0000	0.0000
σ_c/σ_t	0.0000	0.1930	0.8070	0.0000
W_et	0.0000	0.0000	0.0000	1.0000
k_v	0.0000	0.0000	0.7800	0.2200

新窗口打开| 下载CSV

（2）根据式（16）计算指标间距离，计算结果见表4。

表4 各指标间距离

Table 4 Distance between each index

评价指标	σ_θ/σ_c	σ_c/σ_t	W_et	k_v
σ_θ/σ_c	0.0000	0.7055	0.8660	0.7605
σ_c/σ_t	0.7055	0.0000	0.9188	0.2078
W_et	0.8660	0.9188	0.0000	0.7800
k_v	0.7605	0.2078	0.7800	0.0000

新窗口打开| 下载CSV

（3）根据式（17）和式（18）计算指标间信任度。指标间距离越小，指标相互支持程度越大，可信度越高，13个深埋隧洞指标权重见表5。

表5 深埋隧洞指标权重值

Table 5 Index weight of deep buried tunnels

深埋隧洞编号	工程名称	指标权重值
深埋隧洞编号	工程名称	σ_θ/σ_c	σ_c/σ_t	W_et	k_v
1	天生桥二级水电站引水隧洞	0.1896	0.3315	0.1235	0.3554
2	瀑布沟地下水电站地下洞室	0.1693	0.2534	0.3206	0.2567
3	二滩水电站2#支洞	0.2940	0.3451	0.0409	0.3200
4	鲁布革水电站引水隧洞	0.1581	0.4469	0.1048	0.2902
5	李家峡水电站地下洞室	0.4401	0.0715	0.0310	0.4574
6	鱼子溪水电站引水隧洞	0.2878	0.3265	0.1206	0.2651
7	Vietas水电站引水隧洞	0.2277	0.3522	0.1494	0.2707
8	太平驿水电站引水隧洞	0.0524	0.3439	0.2620	0.3417
9	锦屏一级水电站引水隧洞	0.2811	0.2335	0.2837	0.2017
10	猴子岩水电站引水隧洞	0.2877	0.2622	0.2501	0.2000
11	锦屏二级水电站引水隧洞	0.2107	0.2791	0.2179	0.2923
12	龙羊峡水电站地下洞室	0.3664	0.1153	0.0456	0.4726
13	挪威Sima水电站地下厂房	0.1487	0.2104	0.3721	0.2688

新窗口打开| 下载CSV

3.4 预测结果及分析

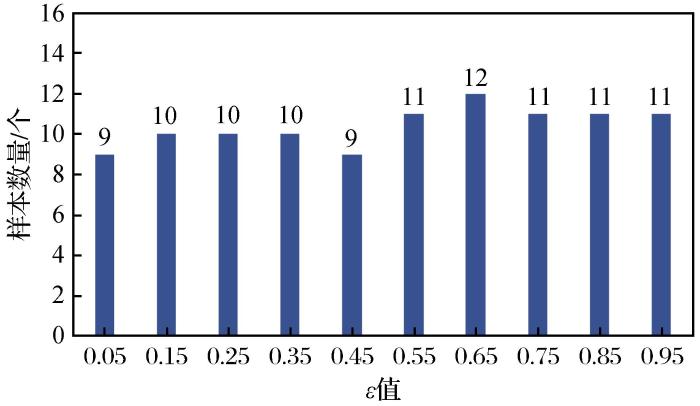
采用置信度识别准则对13个典型深埋隧洞岩爆工程进行等级识别，取置信度λ=0.5。均化系数ε的目的是各指标的综合属性测度在单指标属性测度区间的上限值和下限值取一个均衡的结果，因此ε取值不同，各评价指标属性测度也发生不同程度的变化，对预测准确度会产生一定的影响。为了获得最优ε值，通过收集实际深埋隧洞岩爆工程指标数据进行计算，使ε步长为0.1并在区间［0.05，0.95］选值，最终选择岩爆预测最正确的ε值。由图1可知，样本数据为13个，当ε取值为0.05、0.45时，正确预测岩爆数量为9个，此时预测准确度最低；当ε取值为0.65时，正确预测岩爆数量为12个，此时预测准确度最好，因此本文选择最优ε值为0.65。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 正确预测岩爆个数与ε值的关系

Fig.1 Relationship between the number of rockburst prediction correctly and ε value

当ε值为0.65时，各深埋隧洞的综合属性测度结果见表6。从表6中可以看出，除隧洞编号为8的工程之外，其他深埋隧洞岩爆等级的预测结果与实际情况一致，准确率达到92.31%。对于8号太平驿水电站引水隧洞，根据陈祥等（2009）研究记录，该隧洞共发生400多例岩爆，岩爆等级不定，本文将其判定为强岩爆（Ⅳ），可以采取应力释放钻孔、超前导洞等措施进行超前应力解除，降低岩爆发生的概率。因此，从工程安全角度考虑，将其判定为高等级岩爆是允许的。

表6 岩爆预测评价等级

Table 6 Rockburst prediction evaluation level

深埋隧洞编号	综合属性测度				本文预测结果	实际级别
深埋隧洞编号	$μ_{1}$	$μ_{2}$	$μ_{3}$	$μ_{4}$	本文预测结果	实际级别
1	0.0664	0.3162	0.2836	0.3338	Ⅲ	Ⅲ
2	0.0475	0..2249	0.3162	0.4113	Ⅲ	Ⅲ
3	0.1091	0.4647	0.3853	0.0409	Ⅱ	Ⅱ
4	0.1145	0.4075	0.2977	0.1803	Ⅱ	Ⅰ或Ⅱ
5	0.5742	0.2366	0.1745	0.0147	Ⅰ	Ⅰ
6	0.0023	0.2390	0.5067	0.2520	Ⅲ	Ⅲ
7	0.2528	0.2473	0.2148	0.2551	Ⅱ	Ⅱ
8	0.0165	0.0884	0.3325	0.5626	Ⅳ（误判）	400多例，等级不定
9	0.0901	0.3367	0.4654	0.1078	Ⅲ	Ⅲ
10	0.0935	0.3870	0.3509	0.1686	Ⅲ	Ⅱ或Ⅲ
11	0.0000	0.1209	0.3937	0.4854	Ⅲ	Ⅲ或Ⅳ
12	0.5478	0.2745	0.1372	0.0404	Ⅰ	Ⅰ
13	0.0286	0.1573	0.3447	0.4693	Ⅳ	Ⅲ或Ⅳ

注： $μ 1$ ~ $μ 4$ 表示各深埋隧洞属于Ⅰ~Ⅳ等级的综合属性测度

新窗口打开| 下载CSV

通过模型验算，说明本文提出的正态隶属度—属性区间识别模型对于岩爆倾向等级的预测有一定的实践意义。该模型有以下2个优势：

（1）岩爆的发生与工程地质有很大的关系，在实践中，地质参数通常为一个区间值，与传统模型相比，属性区间识别模型能够更好地适用于各等级指标值为区间的问题，且该模型的准确率有所提升。

（2）指标权重是判定分类结果的重要因素，基于Jousselme距离和指标信任度确定的权重方法考虑了各指标之间、指标与标准等级之间的交互关系的计算方法，因此对于同一指标体系下不同的指标实测值有不同的权重，提高了模型的稳健性。

4 实例验证

双江口水电站位于四川省阿坝藏族羌族自治州马尔康县与金川县交界处，坝高312 m（李航，2020）。地层岩性主要为可尔因花岗岩杂岩体，由钾长石、斜长石、石英、黑云母和白云母等矿物组成，具细—中粒结构，片麻状构造，岩体坚硬完整，含水量少，局部存在断层和挤压破碎带。其中，地下厂房（SPD9）处硐口高程为2 267.6 m，主厂房水平埋深400~640 m，垂直埋深320~500 m，在硐深400 m处测出最大地应力为37.82 MPa，属于高地应力区。SPD9平硐处岩体坚硬完整，裂隙发育稀疏，极易发生岩爆等围岩破坏，因此需要提前进行岩爆倾向等级预判。

通过本文提出的正态隶属度—属性区间识别模型，结合李航（2020）提供的SPD9厂房指标数据实测值对指标权重进行分析，结果见表7。

表7 SPD9洞室指标原始数据及指标权重值

Table 7 Original index and index weight of SPD9 cavern

桩号	评价指标实测值				指标权重值
桩号	σ_θ/σ_c	σ_c/σ_t	W_et	k_v	σ_θ/σ_c	σ_c/σ_t	W_et	k_v
0+123	0.50	10.2	5.0	0.70	0.2510	0.1928	0.3293	0.2269
0+200	0.62	9.4	5.5	0.75	0.1261	0.2878	0.2931	0.2931
0+301	0.57	10.24	5.0	0.70	0.2889	0.1542	0.2889	0.2681
0+406	1.09	10.56	5.5	0.75	0.2582	0.2748	0.2748	0.1923
0+570	0.56	10.61	4.5	0.70	0.3046	0.0817	0.3134	0.3003

新窗口打开| 下载CSV

当ε取值为0.65时，根据指标权重值和式（1）~式（9）计算指标的综合属性测度，同时，根据置信度识别准则，取置信度λ=0.5，得到每个待评价洞段的岩爆预测等级，结果见表8。将本文预测结果与李航（2020）研究结果进行比较，发现本文预测结果与现场实际相吻合，说明本文提出的正态隶属度—属性区间识别模型运用于具体工程实践中是可行且有效的。

表8 SPD9洞室岩爆预测评价等级

Table 8 Rockburst prediction evaluation level of SPD9 cavern

桩号	综合属性测度				本文预测结果	实际级别
桩号	μ₁	μ₂	μ₃	μ₄	本文预测结果	实际级别
0+123	0.0000	0.1276	0.4800	0.3924	Ⅲ	Ⅲ
0+200	0.0000	0.0177	0.5419	0.4404	Ⅲ	Ⅲ
0+301	0.0000	0.1126	0.4633	0.4241	Ⅲ	Ⅲ
0+406	0.0000	0.0000	0.2615	0.7385	Ⅳ	Ⅳ
0+570	0.0000	0.1480	0.4524	0.3996	Ⅲ	Ⅲ

新窗口打开| 下载CSV

5 结论

（1）针对深埋隧洞开挖过程中遇到的岩爆问题，选取应力系数、脆性系数、弹性应变指数和岩石完整性系数作为岩爆倾向等级预测指标，建立了岩爆等级与评价指标之间的对应关系。

（2）采用正态隶属度函数确定指标概率密度，并利用Jousselme距离计算指标间相互距离，计算得到4个不同指标的权重值。与传统赋权方法相比，该方法充分考虑了指标间、指标与标准等级间的联系，对同一指标体系不同工程实例赋予不同权重值，使权重的计算更具科学性。

（3）建立了正态隶属度—属性区间识别模型，将该模型应用到13个典型深埋隧洞工程进行模型准确性测试，并以双江口水电站SPD9厂房为例进行工程实例验证，验证结果精确度较高，表明该模型在实际工程中有一定的应用价值。

中国矿业报

http://www.goldsci.ac.cn/article/2022/1005-2518/1005-2518-2022-30-3-404.shtml

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[]

Adoko

A C

， Gokceoglu

， Wu

，et al，2013.

Knowledge-based and data-driven fuzzy modeling for rockburst prediction

［J］.International Journal of Rock Mechanics and Mining Sciences，61：86-95.

[本文引用: 1]

Chen

Xiang

， Sun

Jinzhong

， Zhang

Jiekun

，et al，2009.

Judgment indexes and classification criteria of rock-burst with the extension judgment method

［J］.China Civil Engineering Journal，42（9）：82-88.

Dong

L J

， Li

X B

， Peng

，2013.

Prediction of rockburst classification using random forest

［J］.Transactions of Nonferrous Metals Society of China，23（2）：472-477.

[本文引用: 1]

Jia

Zheqiang

， Zhang

Yanfei

，et al，2016.

Integrated prediction for rockburst of underground powerhouse of Houziyan hydropower station

［J］.Chinese Journal of Geotechnical Engineering，38（Supp.2）：110-116.

Kidybinski

，1981.

Bursting liability indices of coal

［J］.International Journal of Rock Mechanics and Mining Sciences，18（4）：295-304.

[本文引用: 1]

Hang

，2020.

Research on Tunnel Rockburst Prediction Method Based on Combination Weight Ideal Point Method-Database

［D］.Beijing：China University of Geosciences （Beijing）.

Pengcheng

， Ye

Yicheng

， Wang

Qihu

，et al，2019.

Grey evaluation rockburst prediction model based on normal whitening weight function

［J］.Industrial Minerals & Processing，48（5）：16-22，26.

Renhao

， Gu

Helong

， Li

Xibing

，et al，2020.

A PSO-RBF neural network model for rockburst tendency prediction

［J］.Gold Science and Technology，28（1）：134-141.

Lin

Dayong

， Lei

Mingfeng

， Cao

Haorong

，et al，2018.

Study on construction risk of shield tunnel under-passing existing railway by fuzzy comprehensive evaluation

［J］.Journal of Railway Science and Engineering，15（5）：1347-1355.

Liu

Ran

， Ye

Yicheng

， Zhang

Guangquan

，et al，2019.

Grading prediction model of rockburst based on rough set-multidiensional normal cloud

［J］.Metal Mine，（3）：48-55.

Liu

Xiaoyue

， Yang

Wei

， Zhang

Xuemei

，2021.

Rockburst prediction of multi-dimensional cloud model based on improved hierarchical analytic method and critic method

［J］.Journal of Hunan University（Natural Sciences），48（2）：118-124.

Pei

Qitao

， Li

Haibo

， Liu

Yaqun

，et al，2013.

Rockburst prediction based on a modified grey

［J］.Chinese Journal of Rock Mechanics and Engineering，32（10）：2088-2093.

Russenes

B F

，1974.

Analysis of Rock Spalling for Tunnels in Steep Valley Sides

［D］.Trondheim：Norwegian Institute of Technology.

[本文引用: 1]

Shen

Y N

， Zhang

J B

，2019.

Equipment management performan-ce assessment based on cloud model and evidence theory

［J］.Systems Engineering and Electronics，41（5）：1049-1055.

[本文引用: 1]

Sun

Chensheng

，2019.

A prediction model of rock burst in tunnel based on the improved MATLAB-BP neural network

［J］.Journalof Chongqing Jiaotong University（Natural Science），38（10）：41-49.

Tian

Rui

， Meng

Haidong

， Chen

Shijiang

，et al，2020.

Prediction of intensity classification of rockburst based on deep neural network

［J］.Journal of China Coal Society，45（Supp.1）：191-201.

Wang

M W

， Liu

Q Y

， Wang

，et al，2020.

Prediction of rockburst based on multidimensional connection cloud model and set pair analysis

［J］.International Journal of Geomechanics，20（1）.DOI：10.1061/（ASCE）GM.1943-5622.0001546 .

[本文引用: 1]

Wang

Yingchao

， Jing

Hongwen

， Ji

Xianwei

，et al，2014.

Model for classification and prediction of rock burst intensity in a deep underground engineering with rough set and efficacy coefficient method

［J］.Journal of Central South University（Science and Technology），45（6）：1992-1997.

Wang

Yingchao

， Jing

Hongwen

， Zhang

Qiang

，et al，2015.

A normal cloud model-based study of grading prediction of rockburst intensity in deep underground engineering

［J］.Rock and Soil Mechanics，36（4）：1189-1194.

Wang

Yuanhan

， Li

Wodong

， Li

Qiguang

，et al，1998.

Method of fuzzy comprehensive evaluations for rockburst prediction

［J］.Chinese Journal of Rock Mechanics and Engineering，（5）：15-23.

Chen

， Liu

Xiaoli

， Wang

Enzhi

，et al，2017.

Prediction and classification of strain mode rockburst based on five-factor crierion and combined weight-ideal point method

［J］.Chinese Journal of Geotechnical Engineering，39（12）：2245-2252.

Yin

Xin

， Liu

Quansheng

， Wang

Xinyu

，et al，2020.

Prediction model of rockburst intensity classification based on combined weighting and attribute interval recognition theory

［J］.Journal of China Coal Society，45（11）：3772-3780.

Zhang

Biao

， Dai

Xingguo

，2017.

rockburst intensity grade based on index distance and uncertainty measure

［J］.Rock and Soil Mechanics，38（Supp.2）：257-265.

Zhang

Guangcun

， Gao

Qian

， Du

Juqiang

，et al，2013.

Rockburst criterion based on artificial neural networks and nonlinear regression

［J］.Journal of Central South University（Science and Technology），44（7）：2977-2981.

Zhang

Jingjian

， Fu

Bingjun

，2008.

Rock burst and its criteria and control

［J］.Chinese Journal of Rock Mechanics and Engineering，27（10）：2034-2042.

Zhang

Lewen

， Zhang

Deyong

， Qiu

Daohong

，2010.

Application of extension evaluation based on rough set in rockburst prediction

［J］ .Coal Coal Journal，35（9）：1461-1465.

ZhangYan， Su

Guoshao

， Yan

Liubin

，2011.

Method of identifying rockburst grades based on Gaussian process machine learning

［J］.Chinese Journal of Underground Space and Engineering，7（2）：392-397.

Zou

Qiang

， Zhou

Jianzhong

， Yang

Xiaoling

，et al，2011.

A comprehensive assessment model for severity degree of dam failure impact based on attribute interval recognition theory

［J］.Journal of Sichuan University （Engineering Science Edition），43（2）：45-50.

陈祥，孙进忠，张杰坤，等，2009.

岩爆的判别指标和分级标准及可拓综合判别方法

［J］.土木工程学报，42（9）：82-88.

[本文引用: 1]

贾哲强，张茹，张艳飞，等，2016.

猴子岩水电站地下厂房岩爆综合预测研究

［J］.岩土工程学报，38（增2）：110-116.

李航

，2020.

基于组合权重理想点法—数据库的隧洞岩爆预测方法研究

［D］.北京：中国地质大学（北京）.

[本文引用: 3]

李鹏程，叶义成，王其虎，等，2019.

基于正态白化权函数的灰评估岩爆预测模型

［J］.化工矿物与加工，48（5）：16-22，26.

李任豪，顾合龙，李夕兵，等，2020.

基于PSO-RBF神经网络模型的岩爆倾向性预测

［J］.黄金科学技术，28（1）：134-141.

[本文引用: 1]

林大涌，雷明锋，曹豪荣，等，2018.

盾构下穿运营铁路施工风险模糊综合评价方法研究

［J］.铁道科学与工程学报，15（5）：1347-1355.

[本文引用: 1]

刘冉，叶义成，张光权，等，2019.

岩爆分级预测的粗糙集—多维正态云模型

［J］.金属矿山，（3）：48-55.

刘晓悦，杨伟，张雪梅，2021.

基于改进层次法与CRITIC法的多维云模型岩爆预测

［J］.湖南大学学报（自然科学版），48（2）：118-124.

[本文引用: 1]

裴启涛，李海波，刘亚群，等，2013.

基于改进的灰评估模型在岩爆中的预测研究

［J］.岩石力学与工程学报，32（10）：2088-2093.

[本文引用: 1]

孙臣生

，2019.

基于改进MATLAB-BP神经网络算法的隧道岩爆预测模型

［J］.重庆交通大学学报（自然科学版），38（10）：41-49.

[本文引用: 1]

田睿，孟海东，陈世江，等，2020.

基于深度神经网络的岩爆烈度分级预测研究

［J］.煤炭学报，45（增1）：191-201.

[本文引用: 1]

王迎超，靖洪文，吉咸伟，等，2014.

深埋地下工程岩爆烈度分级预测的RS-功效系数模型

［J］.中南大学学报（自然科学版），45（6）：1992-1997.

[本文引用: 1]

王迎超，靖洪文，张强，等，2015.

基于正态云模型的深埋地下工程岩爆烈度分级预测研究

［J］.岩土力学，36（4）：1189-1194.

[本文引用: 1]

王元汉，李卧东，李启光，等，1998.

岩爆预测的模糊数学综合评判方法

［J］.岩石力学与工程学报，（5）：15-23.

[本文引用: 2]

徐琛，刘晓丽，王恩志，等，2017.

基于组合权重—理想点法的应变型岩爆五因素预测分级

［J］.岩土工程学报，39（12）：2245-2252.

殷欣，刘泉声，王心语，等，2020.

基于组合赋权和属性区间识别理论的岩爆烈度分级预测模型

［J］.煤炭学报，45（11）：3772-3780.

[本文引用: 2]

张彪，戴兴国，2017.

基于指标距离与不确定度量的岩爆云模型预测研究

［J］.岩土力学，38（增2）：257-265.

张光存，高谦，杜聚强，等，2013.

基于人工神经网络及非线性回归的岩爆判据

［J］.中南大学学报（自然科学版），44（7）：2977-2981.

[本文引用: 1]

张镜剑，傅冰骏，2008.

岩爆及其判据和防治

［J］.岩石力学与工程学报，27（10）：2034-2042.

[本文引用: 1]

张乐文，张德永，邱道宏，2010.

基于粗糙集的可拓评判在岩爆预测中的应用

［J］.煤炭学报，35（9）：1461-1465.

[本文引用: 1]

张研，苏国韶，燕柳斌，2011.

基于高斯过程机器学习的岩爆等级识别方法

［J］.地下空间与工程学报，7（2）：392-397.

邹强，周建中，杨小玲，等，2011.

属性区间识别模型在溃坝后果综合评价中的应用

［J］.四川大学学报（工程科学版），43（2）：45-50.

[本文引用: 1]

Knowledge-based and data-driven fuzzy modeling for rockburst prediction

2013

... 多年来，众多学者对岩爆预测展开了诸多研究.早期岩爆预测研究只考虑单一因素的影响，如：岩石刚度、强度和能量等，且国内外学者提出了不同的判据，如：Russense判据（张镜剑等，2008）和Kidybinski判据（Kidybinski，1981）等.然而，岩爆发生受多种因素共同制约，单一判据具有片面性.随着岩爆灾害研究工作的深入，岩爆发生的影响因素与岩爆倾向等级的非线性关系逐渐引起学者们的关注，新的数学方法及智能算法模型开始应用到岩爆预测过程中.数学方法主要有模糊综合评判法（Adoko et al.，2013；王元汉等，1998）、物元可拓理论（张乐文等，2010）、灰色系统理论（裴启涛等，2013）、功效系数法（王迎超等，2014）和云模型（王迎超等，2015）等.智能算法主要有BP神经网络（孙臣生，2019）、人工神经网络（张光存等，2013）、深度神经网络（田睿等，2020）和随机森林方法（Dong et al.，2013）等. ...

Judgment indexes and classification criteria of rock-burst with the extension judgment method

2009

Prediction of rockburst classification using random forest

2013

Integrated prediction for rockburst of underground powerhouse of Houziyan hydropower station

2016

Bursting liability indices of coal

1981

Research on Tunnel Rockburst Prediction Method Based on Combination Weight Ideal Point Method-Database

2020

Grey evaluation rockburst prediction model based on normal whitening weight function

2019

A PSO-RBF neural network model for rockburst tendency prediction

2020

Study on construction risk of shield tunnel under-passing existing railway by fuzzy comprehensive evaluation

2018

Grading prediction model of rockburst based on rough set-multidiensional normal cloud

2019

Rockburst prediction of multi-dimensional cloud model based on improved hierarchical analytic method and critic method

2021

Rockburst prediction based on a modified grey

2013

Analysis of Rock Spalling for Tunnels in Steep Valley Sides

1974

... 内因和外因共同作用造成岩爆灾害.其中，内因是指岩石的物理力学性质，外因是指不同的开挖方式造成岩石应力重分布.目前，关于岩爆等级评价指标的选择国内外没有统一的理论标准，因此本文在参考大量岩爆实例和已有岩爆判据（Wang et al.，2020；Russenes，1974）的基础上，选择4个评价指标：（1）应力系数，即岩石最大切向应力与单轴抗压强度之比σ_θ/σ_c，比值大小代表岩体的强度条件，而岩爆灾害多发生于硬岩条件下；（2）脆性系数，即岩石单轴抗压强度与抗拉强度之比σ_c/σ_t，比值大小代表岩体的稳定性条件，稳定性越差则岩爆程度越严重；（3）弹性应变指数W_et，反映了岩石储存弹性变形势能的能力，数值越大则发生岩爆灾害的倾向性越大；（4）岩石完整性系数k_v，岩石完整性越好，越容易储存应变能量，发生岩爆灾害的倾向性也越大. ...

Equipment management performan-ce assessment based on cloud model and evidence theory

2019

... 设I_i 和I_j 为指标集合中的2个评价指标，则其对应的各等级概率密度为m_i 和m_j，计算指标I_i 和I_j 之间的Jousselme距离d_ij （Shen et al.，2019），表示为 ...

A prediction model of rock burst in tunnel based on the improved MATLAB-BP neural network

2019

Prediction of intensity classification of rockburst based on deep neural network

2020

Prediction of rockburst based on multidimensional connection cloud model and set pair analysis

2020

Model for classification and prediction of rock burst intensity in a deep underground engineering with rough set and efficacy coefficient method

2014

A normal cloud model-based study of grading prediction of rockburst intensity in deep underground engineering

2015

Method of fuzzy comprehensive evaluations for rockburst prediction

1998

Prediction and classification of strain mode rockburst based on five-factor crierion and combined weight-ideal point method

2017

Prediction model of rockburst intensity classification based on combined weighting and attribute interval recognition theory

2020

rockburst intensity grade based on index distance and uncertainty measure

2017

Rockburst criterion based on artificial neural networks and nonlinear regression

2013

Rock burst and its criteria and control

2008

Application of extension evaluation based on rough set in rockburst prediction

2010

Method of identifying rockburst grades based on Gaussian process machine learning

2011

A comprehensive assessment model for severity degree of dam failure impact based on attribute interval recognition theory

2011

岩爆的判别指标和分级标准及可拓综合判别方法

2009

... 当ε值为0.65时，各深埋隧洞的综合属性测度结果见表6.从表6中可以看出，除隧洞编号为8的工程之外，其他深埋隧洞岩爆等级的预测结果与实际情况一致，准确率达到92.31%.对于8号太平驿水电站引水隧洞，根据陈祥等（2009）研究记录，该隧洞共发生400多例岩爆，岩爆等级不定，本文将其判定为强岩爆（Ⅳ），可以采取应力释放钻孔、超前导洞等措施进行超前应力解除，降低岩爆发生的概率.因此，从工程安全角度考虑，将其判定为高等级岩爆是允许的. ...

猴子岩水电站地下厂房岩爆综合预测研究

2016

基于组合权重理想点法—数据库的隧洞岩爆预测方法研究

2020

... 双江口水电站位于四川省阿坝藏族羌族自治州马尔康县与金川县交界处，坝高312 m（李航，2020）.地层岩性主要为可尔因花岗岩杂岩体，由钾长石、斜长石、石英、黑云母和白云母等矿物组成，具细—中粒结构，片麻状构造，岩体坚硬完整，含水量少，局部存在断层和挤压破碎带.其中，地下厂房（SPD9）处硐口高程为2 267.6 m，主厂房水平埋深400~640 m，垂直埋深320~500 m，在硐深400 m处测出最大地应力为37.82 MPa，属于高地应力区.SPD9平硐处岩体坚硬完整，裂隙发育稀疏，极易发生岩爆等围岩破坏，因此需要提前进行岩爆倾向等级预判. ...

... 通过本文提出的正态隶属度—属性区间识别模型，结合李航（2020）提供的SPD9厂房指标数据实测值对指标权重进行分析，结果见表7. ...

... 当ε取值为0.65时，根据指标权重值和式（1）~式（9）计算指标的综合属性测度，同时，根据置信度识别准则，取置信度λ=0.5，得到每个待评价洞段的岩爆预测等级，结果见表8.将本文预测结果与李航（2020）研究结果进行比较，发现本文预测结果与现场实际相吻合，说明本文提出的正态隶属度—属性区间识别模型运用于具体工程实践中是可行且有效的. ...

基于正态白化权函数的灰评估岩爆预测模型

2019

基于PSO-RBF神经网络模型的岩爆倾向性预测

2020

... 岩爆是一种发生在深埋隧洞中的常见地质灾害，是隧洞开挖工程中由于岩体本身积聚的应变能量超过岩体破坏时消耗的能量，岩石受到应力重分布作用将多余能量释放出来致使岩石发生爆裂、剥离的现象（李任豪等，2020）.岩爆是高地应力地区常见的地质现象，最早发生在矿井中，后来随着大量深埋隧洞修建于高地应力区域，岩爆问题受到了矿山和隧道工程领域研究人员的重视.为了降低岩爆灾害对作业人员及机械的损害程度，探寻科学、合理的岩爆倾向等级预测方法对岩爆防控具有极其重要的意义. ...

盾构下穿运营铁路施工风险模糊综合评价方法研究

2018

... 评价对象的性质决定评价指标，模糊理论的关键是建立指标隶属度函数（林大涌等，2018）.正态隶属度函数具有模糊性，且能够减少主观因素的影响，因此本文采用正态隶属度函数来确定岩爆评价指标属于某评价等级的隶属度，具体公式如下： ...

岩爆分级预测的粗糙集—多维正态云模型

2019

基于改进层次法与CRITIC法的多维云模型岩爆预测

2021

... 以上评价指标相互独立又相互关联，参照王元汉等（1998）、殷欣等（2020）和刘晓悦等（2021）的研究，将岩爆等级划分为4个区间，即：无岩爆（Ⅰ级）、弱岩爆（Ⅱ级）、中等岩爆（Ⅲ级）和剧烈岩爆（Ⅳ级），并确定了岩爆等级与评价指标之间的关系，如式（20）所示.由式（20）可以看出，每个评价指标集的端点值均满足

a_{j 1} < a_{j 2} < \dots < a_{j k}, b_{j 1} < b_{j 2} < \dots < b_{j k}

，因此可以判定岩爆倾向等级预测属于典型的有序分割类问题. ...

基于改进的灰评估模型在岩爆中的预测研究

2013

基于改进MATLAB-BP神经网络算法的隧道岩爆预测模型

2019

基于深度神经网络的岩爆烈度分级预测研究

2020

深埋地下工程岩爆烈度分级预测的RS-功效系数模型

2014

基于正态云模型的深埋地下工程岩爆烈度分级预测研究

2015

岩爆预测的模糊数学综合评判方法

1998

a_{j 1} < a_{j 2} < \dots < a_{j k}, b_{j 1} < b_{j 2} < \dots < b_{j k}

，因此可以判定岩爆倾向等级预测属于典型的有序分割类问题. ...

基于组合权重—理想点法的应变型岩爆五因素预测分级

2017

基于组合赋权和属性区间识别理论的岩爆烈度分级预测模型

2020

... 岩爆倾向等级预测属于多属性有序分割类问题，通过分析现有数学方法和智能算法，发现智能算法应用简单，计算过程全部由软件驱动，但是部分智能算法由于初始化随机权重使得计算结果不稳定.而数学方法可以避免该缺点，其中属性区间识别模型在解决多属性有序分割类问题上具有明显的优越性（殷欣等，2020）.因此，本文引入属性区间识别模型进行岩爆倾向等级预测.为了避免权重计算出现前述问题，本文采用正态隶属度函数计算指标概率密度，并利用Jousselme公式计算指标间距离，进而确定指标权重.该方法从各指标所属各等级的距离出发，综合考虑各指标各等级间的相互影响程度，对同一指标体系下不同工程实例赋予不同权重值，使得权重计算相对更加合理.最后，应用13个典型深埋引水隧洞案例进行模型准确性测试，并以双江口水电站SPD9厂房为例进行了工程实例验证，结果表明该模型预测结果能够客观反映岩爆实际结果，可为预测类似深埋引水隧洞岩爆倾向等级提供新思路. ...

a_{j 1} < a_{j 2} < \dots < a_{j k}, b_{j 1} < b_{j 2} < \dots < b_{j k}

，因此可以判定岩爆倾向等级预测属于典型的有序分割类问题. ...

基于指标距离与不确定度量的岩爆云模型预测研究

2017

基于人工神经网络及非线性回归的岩爆判据

2013

岩爆及其判据和防治

2008

基于粗糙集的可拓评判在岩爆预测中的应用

2010

基于高斯过程机器学习的岩爆等级识别方法

2011

属性区间识别模型在溃坝后果综合评价中的应用

2011

... 将均化系数（邹强等，2011）引入属性测度区间，计算各指标的综合属性测度

μ_{i j p}

，表示为 ...

〈

〉