经济的快速发展导致世界各国对矿产资源的需求量不断增大，传统的采矿方式已难以满足现代社会的要求。21世纪初，一些发达国家纷纷开始布局智能化、无人化采矿，我国在“十二五”期间也实施了智能采矿领域的多项技术攻关并获得突破，智能采矿和无人化采矿已成为采矿技术发展的一大趋势（Wang et al.，2017；Li et al.，2018）。采矿设备的可靠性分析是采矿技术研究的一个重要课题。通过评估和分析能够及早发现潜在故障点，确保设备高效运行，减少故障和事故的发生。在智能采矿和无人化采矿快速发展的大背景下，智能采矿设备的可靠性分析更为重要。智能采矿设备通常集成了大量的传感器、控制系统和自动化功能，这些技术的运行稳定性和准确性直接关系到采矿作业的效率和安全。重视和深入进行智能采矿设备的可靠性分析，将有助于推动采矿技术的创新和进步，为行业带来更多的机遇和发展潜力。

国内外对设备系统的可靠性分析均有一定的研究，并已充分应用于各行各业的生产实践当中。根据设备自身的特点以及可靠性参数获取量的不同，采取的分析方法也不同。目前可靠性分析方法主要有故障树、可靠性框图、贝叶斯网络、马尔科夫链和蒙特卡洛仿真等（Li et al.，2012；Gao et al.，2021；Leite et al.，2022）。可靠性分析的方法在不同的行业均具有适用性，但在应用过程中通常需要针对具体的设备系统进行优化，这种做法提高了评估的准确性，也为后续其他学者的可靠性研究提供了更有价值的参考（Barabady et al.，2008；Dong et al.，2018；柯愈贤等，2018）。在对矿用设备的可靠性分析中，选择合适的建模方法，计算设备的故障率和维修间隔时间等可靠性指标，对设备可靠性进行预测，能够有效提高生产效率和安全性。如Hoseinie et al.（2012）根据现场数据和机器设计对采煤机进行可靠性建模，对子系统和机器的可靠性进行了评估。Furuly et al.（2013）讨论了比例危险模型（PHM）的应用，以量化气候条件对挪威斯瓦尔巴特群岛Svea煤矿堆垛机皮带危险率的影响。Vayenas et al.（2014）将离散分布函数引入软件工具（GenRel），对2台矿井提升机的动态可靠性进行预测，结果表明在给定置信水平5%下2台提升机的动态可靠性可接受。当前，在分析中引入机器学习的方法，通过开发算法模型实现更先进的统计，并对大规模的数据进行准确高效的处理，是可靠性研究的一个主流方向（Samatemba et al.，2020；Saymon et al.，2021；Odeyar et al.，2022）。然而，当前研究大多是针对某设备或其中重要部件的设计可靠性进行分析，对于设备在投入使用后在实际运行环境中的状态缺少系统分析。同时，由于智能采矿设备发展较晚，对其可靠性的分析研究更为匮乏。

因此，本文以山东黄金集团三山岛金矿智能铲运系统为研究案例，对智能采矿设备的可靠性进行分析，全面考虑了设备在实际运行环境中所受到的多方面因素的影响。通过采用模糊故障树分析与蒙特卡洛仿真相结合的研究方法，对系统可靠性的动态规律进行分析。主要目标包括：计算该智能采矿设备的故障发生概率，分析该设备常见的故障模式，通过可靠性仿真探究设备在动态时间内运行使用故障的规律并分析导致故障发生的主要事件。

山特维克智能柴油铲运机LH410行驶载重能力为10 t，举升铲取力为20.39 t，翻斗铲取力为19.34 t，倾翻荷载为23.40 t，标准斗容为4.0 m³。设备尺寸为9.70 m×2.55 m×2.40 m，转弯半径为内径3 283 mm，外径6 518 mm。LH410具有很大的举升高度，能够配合TH430卡车进行快速、准确的三斗满装作业。

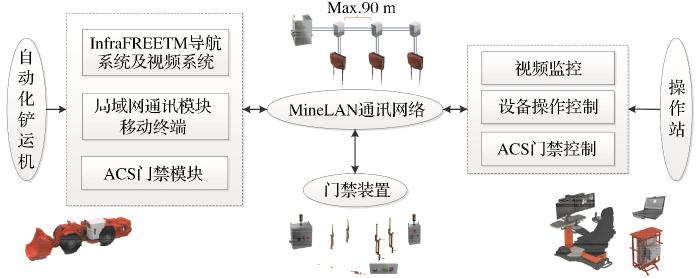
矿山采用AUTOMINE® Lite自动化出矿系统，主要系统部件包括如下4个部分：

（1）操作站：用于操作人员控制系统及查看用户地图界面。

（2）门禁控制系统（ACS）：布置进入屏障以便控制进入自动化运行区域的人员和设备。

（3）MineLAN通讯网络：100%覆盖整个铲运机运行的生产区域，为AutoMine®子系统和自动化铲运机之间提供可靠且稳定的无线网络连接。

（4）自动化铲运机：铲运机配有InfraFREETM导航及视频系统，部件还包含MineLAN矿山局域网通讯模块移动终端和ACS门禁模块。

系统构架如图1所示。在系统运行过程中，通过对出矿区域和路线进行准确规划，将操作人员和设备安置在各自的合适区域内，可以安全、高效地完成出矿作业。通过MineLAN通讯网络实现对生产区域网络的全覆盖，操作人员在操作站便可进行远程操作和视频监控。

以智能铲运系统运行使用故障作为顶事件，建立的故障树需要考虑设备本身可能产生的机械故障，由于管理和操作所带来的使用故障，以及由于井下复杂工况环境所造成的使用故障等。经过统计，得到该系统自投入生产以来记录到的故障数据如表1所示。

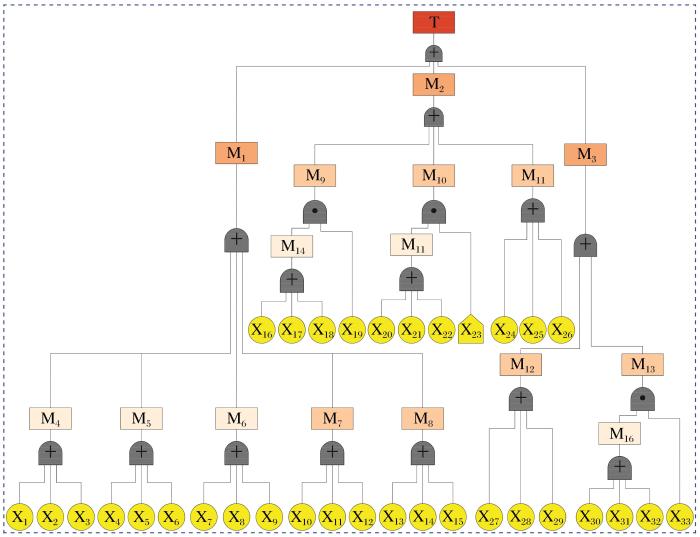
对系统目前已发生的故障进行分类，其中智能铲运系统使用故障34次、设计管理故障13次和其他原因故障16次。因此，以这3个事件作为智能铲运系统运行故障树的一级事件。对现有的故障原因进行进一步划分，得到相应的二级事件（表2中的M₄~M₁₃）。对具体的故障原因进行整理和归纳，使其分类清晰且符合底事件标准，得到24项底事件（表3中的X₁~X₁₁、X₁₃、X₁₅、X₁₆、X₁₉、X₂₀、X₂₂、X₂₅~X₃₁）。由于现有发生的故障较少，并不能涵盖所有可能导致系统故障的原因事件，因此在原有故障事件的基础上，还需要参考大量的文献资料（隋宝峰等，2014；任军，2017；李兆猛，2018；郇双宇等，2019），并进行实地考察调研，补充完善故障树。通过组织相关评估专家以及矿山工作人员对建立的故障树模型进行详细探讨，并反复修改以符合矿山设备实际运行情况。最终，在原有事件的基础上，补充了9项底事件（表3中的X₁₂、X₁₄、X₁₇、X₁₈、X₂₁、X₂₃、X₂₄、X₃₂、X₃₃）和3项中间事件（表2中的M₁₄~M₁₆），并审查各底事件之间的逻辑关系，以及中间事件与底事件之间的逻辑关系，用准确的逻辑门符号进行表达。采取自上而下的分析方式对智能铲运系统运行使用故障进行分析，得出中间事件16个（表2），底事件33个（表3）。采用逻辑与门和逻辑或门构建的故障树模型如图2所示。

底事件概率的求取采用模糊集合理论的方法，具体求取步骤如下：（1）采用专家调查法对底事件进行评价，得出语言评价值；（2）将语言评价值转化为故障概率的梯形模糊数并进行汇总；（3）对模糊数进行去模糊化处理，并转化为失效概率。

专家调查法共选取了10位采矿领域的专家，包括高校教授、矿山管理者、高级工程师和工程师，这些专家具有丰富的科研和实践工作经验。专家信息如表4所示。根据各专家的知识水平、职称、工作经验及与该设备运行系统的相关性，对专家评价结果进行权重划分，将计算系数进行归一化处理得到计算权重。评定结果如表5所示。

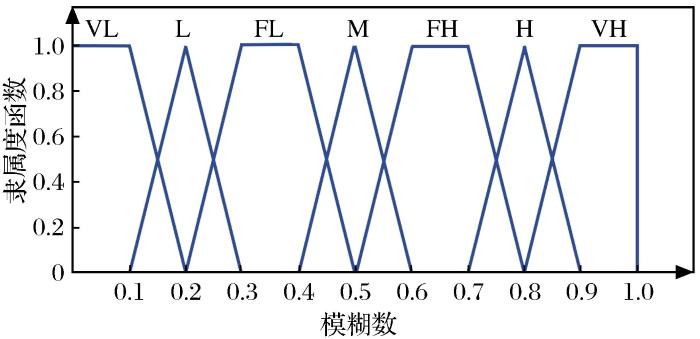
在专家对故障树底事件发生概率的评价中，将语言评价值定义为7个等级，分别为：｛非常低，低，比较低，中等，比较高，高，非常高｝。为了方便图形表示，以7个等级英语单词的前面1~2个字母进行表示，依次为：｛VL，L，FL，M，FH，H，VH｝。对评价值进行区间均匀分度，将其转化为模糊数，根据语言值及其对应的隶属函数，得到故障发生概率的模糊数如图3所示。

以底事件X₁（电机模块温度过高）为例，依据专家调查结果求取并汇总得出底事件概率。专家意见及对应权重如表6所示。

所有专家意见的汇总结果可表示为

式中：RXi为底事件X _i 的专家意见综合结果；m为专家数；i 为底事件序数；j为专家意见序数；（l_i，j，m_i，j，u_i，j，t_i，j ）为对第i个底事件第j个专家的专家意见对应的模糊数；w_i，j 为对应专家的计算权重。

采用式（1）对10位专家关于底事件X₁（电机模块温度过高）的意见的模糊数进行计算，得到结果为（0.08413，0.14875，0.20364，0.30364）。

将梯形模糊数（l，m，u，t）去模糊化，并转化为失效概率，需要先通过模糊数得到底事件的脆失效概率（CFP），再进一步转化为失效概率（FP）。脆失效概率和失效概率的求解公式（Onisawa，1988）分别为

式中：CFP为脆失效概率；l、m、u和t分别为梯形模糊数的第一、二、三、四项；FP为失效概率。

利用式（2）和式（3）对底事件X₁的模糊数进行处理，得到脆失效概率和失效概率分别为0.186809和0.000175。

采取同样的方法，将底事件X₂~X₁₀的专家意见进行汇总，并采用式（2）和式（3）进行去模糊化再转化为失效概率。最后求得所有底事件的脆失效概率和失效概率如表7所示。

采用布尔代数法对故障树进行化简，得到其最小割集如表8所示。

根据表8中的最小割集进行计算，将所有的底事件视为相互独立的事件，则顶事件概率计算公式为

式中：g为顶事件发生概率；NG为系统中最小割集数；r为最小割集序数；i 为底事件序数；xi∈Gr为第i个底事件属于第r个最小割集；qi为第i个底事件的概率。

计算得到的顶事件发生概率即为智能铲运系统运行使用故障概率，结果为0.3481%。由表1可知，实际故障概率为0.4598%，计算结果与实际运行结果相差约0.1%，说明计算得出的智能铲运系统运行使用故障概率与矿山实际运行情况相符合，验证了计算方法和模型的有效性。

对故障树的定量计算可以得到系统的故障概率，然而，计算结果只能表示系统在某一时刻下的可靠度，具有较大的局限性。为了更好地解决智能铲运系统在运行使用过程中的各种可靠性问题，需要分析智能铲运系统随时间响应的实时动态可靠性指标。为此，采用蒙特卡洛仿真的方法，对该系统的动态可靠性进行分析。

蒙特卡洛方法是一种通过生成随机数来实现对复杂系统进行评估的计算仿真模拟方法，该方法已广泛运用于诸多领域之中，用以解决实际的工程问题。在工业生产、环境治理、灾害预防和矿业生产等方面，该方法在复杂系统的可用性评估和故障诊断方面具有很高的应用价值（Boiarkina et al.，2017；Ramesh et al.，2021；Chudasama，2022；Li et al.，2022）。本文基于对智能铲运系统的故障树分析，运用蒙特卡洛的方法原理，分析计算系统的平均无故障时间、可靠度、不可靠度、失效概率和底事件重要度等参数。

蒙特卡洛方法的分析过程通常包括3个步骤：（1）建立模型。模型的解为需要得到的各项参数指标，且需要设定一个固定的时间增量，以此分析系统的动态过程。（2）随机抽样。该抽样以计算机生成的伪随机数代替真实的随机数，随机数的生成特征应当符合实际的概率分布。（3）统计指标。需要分析的系统参数往往不止一个，模型的输出结果也可能包含估计值、区间和数值分布等，然后统计计算模型最终解。

在智能铲运系统运行使用故障树中共有i（i=33）个底事件，用X _i 来表示每一个底事件。λ_i 表示每一个底事件的失效率，λ表示智能铲运系统运行使用故障的概率，用t来表示系统的运行时间，假设该故障树中所有底事件均服从指数分布。以二态系统来分析该故障树，即设定故障树中所有事件的故障状态只有“故障”和“正常”2种，且底事件之间相互独立。用x_i 来表示底事件X _i 的故障状态，用Y来表示顶事件的故障状态。

智能铲运系统运行使用故障树的结构函数为Y（t）=［x₁（t），x₂（t），x₃（t），…，x_i （t）］，可以看出，当底事件的状态确定时，顶事件Y的状态也随之确定。

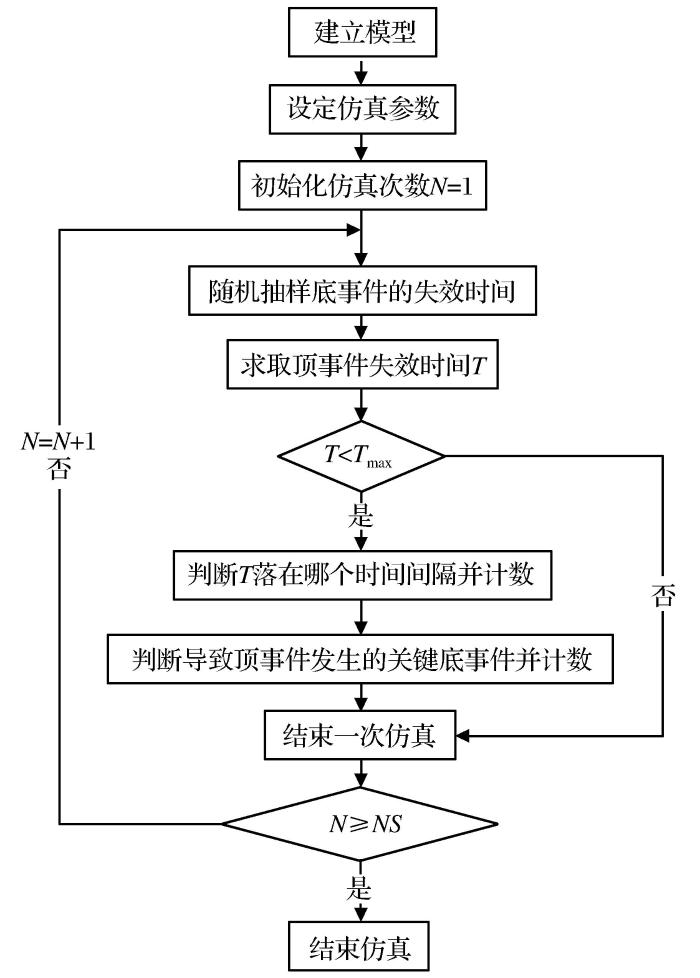
因此，设计仿真步骤如下：

步骤1：确定仿真参数。仿真参数包括最大运行时间T_max、时间间隔数m和仿真次数NS。最大运行时间需要先进行假设，其数值需要保证在绝大多数仿真结果中，系统的仿真寿命均落在这个区间内且不宜过大，以免影响结果的展现，经过多次模拟，将最大运行时间设定为1 000 h。在模拟中，以点代表相应的时间段，将最大运行时间分成的时间段数为时间间隔数，时间间隔数设定为1 000，则最大运行时间被划分为1 000个区间，且每个区间的时长为1 h。仿真次数同样需要足够大以保证结果的精度，经过模拟对比，设定仿真次数为10 000次。

步骤2：随机抽样。假设底事件服从指数分布，求取特征寿命并在每次仿真中生成一组参数矩阵，该矩阵即为在该次仿真下各底事件的随机寿命。

步骤3：求取顶事件寿命。根据故障树的结构对各底事件进行排序，按照底事件之间的逻辑关系找出每次仿真中导致顶事件发生的关键事件寿命，即可得到顶事件寿命。

步骤4：确定区间。当顶事件寿命在最大运行时间之外时，该次仿真失效。记录未失效仿真中顶事件寿命所在区间和导致顶事件发生的关键底事件。

步骤5：重复上述步骤2至步骤4，多次仿真，直至达到设定次数。仿真流程如图4所示。

（1）平均无故障时间MTBF：指每2次相邻故障之间的工作时间的数学期望值，相当于系统的工作时间与这段时间内的故障数的比值。在仿真中，其计算公式为

式中：MTBF为平均无故障时间；NS为设定仿真次数；j为仿真次数序数；tk为顶事件寿命所在区间。

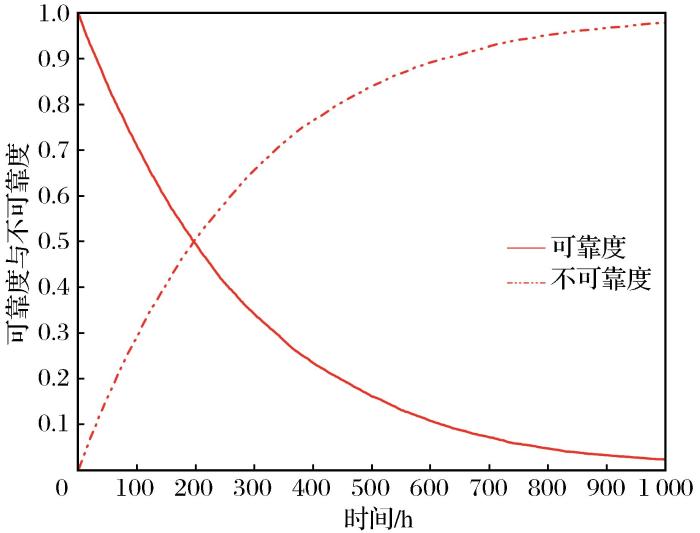
（2）系统的可靠度与不可靠度：统计从开始到各个时间间隔内顶事件发生的总次数，在每段时间间隔内的顶事件发生总次数对总仿真次数的占比即为该段时间间隔内的系统不可靠度，系统可靠度则为顶事件未发生的总次数在总仿真次数中的占比。

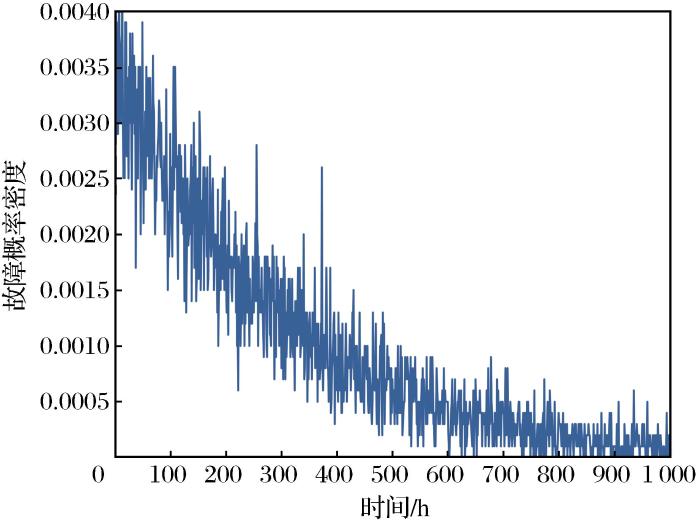
（3）系统的失效概率密度：指在该段时间内的顶事件发生的次数对总仿真次数的占比，可以反映故障概率随时间的变化趋势。

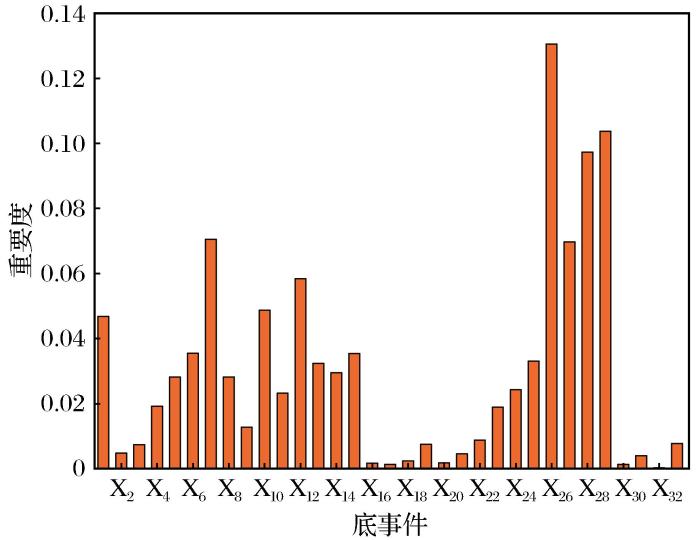
（4）底事件的重要度：分别统计由于各个底事件所导致顶事件发生的次数，以该次数在顶事件发生次数中的占比来表示各底事件的仿真重要度，通过对仿真重要度进行排序可以找出导致顶事件发生的重要事件。

根据上述原理和方法，使用MATLAB数值模拟软件，编写蒙特卡洛仿真算法，对智能铲运系统运行使用进行仿真模拟，结果如下：

（1）平均无故障时间为270 h，将结果与表1中的实际平均无故障时间进行对比分析，计算得到符合度为97.1%，验证了仿真模拟的精度。

（2）可靠度与不可靠度曲线如图5所示。由图5可以看出，系统的可靠度随时间的增加呈不断降低趋势，且降低速度越来越慢。在133 h时，可靠度降低至0.631，此时判定该系统不可靠，需要进行维护；在279 h时，可靠度降低至0.368，若不加维护地运行系统至该状态，将会导致系统运行失效。

（3）失效概率分布如图6所示。可以看出，系统的失效概率同样随着时间的增加越来越小，时间为0时失效概率最大，数值在0.0035左右；到900 h时，失效概率已经接近于0。

（4）底事件重要度仿真结果如图7所示。由图7可知，在导致智能铲运系统运行使用故障的各项底事件中，影响最大的因素为管理原因X₂₆（操作规范不合格）和人员原因X₂₉（信息沟通失误），个人原因X₂₈（工作不专注）和X₂₇（安全意识欠缺）的影响也较大，从机械设计的角度，X₇（操作装置故障）和X₁₂（制动系统老化）为影响最大的因素。从这6个方面入手进行管理，易减少系统故障的发生。

（1）采用模糊故障树的方法对系统可靠性进行分析计算，得出各底事件的发生概率，进而得到系统故障概率为0.3481%。

（2）采用蒙特卡洛算法对故障树进行仿真模拟，得到系统平均无故障时间为270 h。通过分析仿真结果获得了系统可靠性、不可靠性以及系统失效概率随时间变化的动态结果，更好地反映了系统可靠性变化的过程和阶段，其中系统可靠性变化的关键节点为133 h和279 h时，该结果能够为系统生产运行提供有效指导。同时，通过计算各底事件的仿真重要度，得出底事件中影响较大的因素，为工业实际提供参考。

（3）将系统故障概率理论计算结果与实际值进行对比，误差约为0.1%，验证了故障模型和计算方法的准确性。将仿真平均无故障时间与实际平均无故障时间进行对比分析，符合度为97.1%，验证了仿真模拟的有效性和精度。