外荷载下青砂岩声发射特征及损伤演化规律

图1 岩石试样

Fig.1 Rock samples

表1 岩石试样基本物理参数

Table 1 Basic physical parameters of rock samples

岩性	试样编号	直径/mm	高度/mm	形状
青砂岩	QSY₁	49.22	100.28	圆柱体
	QSY₂	49.32	99.80	圆柱体
	QSY₃	49.24	100.34	圆柱体

1.2 试验装置、方法及参数设置

（1）试验装置。单轴压缩声发射试验设备主要有加载设备（a）、变形采集仪（b）和AE声发射系统（c），如图2所示；纽迈MiniMR-60核磁共振仪由信号接收设备（a）和岩样检测设备（b）组成，如图3所示。

图2

图2 单轴压缩声发射试验设备

Fig.2 Uniaxial compression acoustic emission test equipment

图3

图3 纽迈MiniMR-60核磁共振检测仪

Fig.3 Newman MiniMR-60 nuclear magnetic resonance scanner

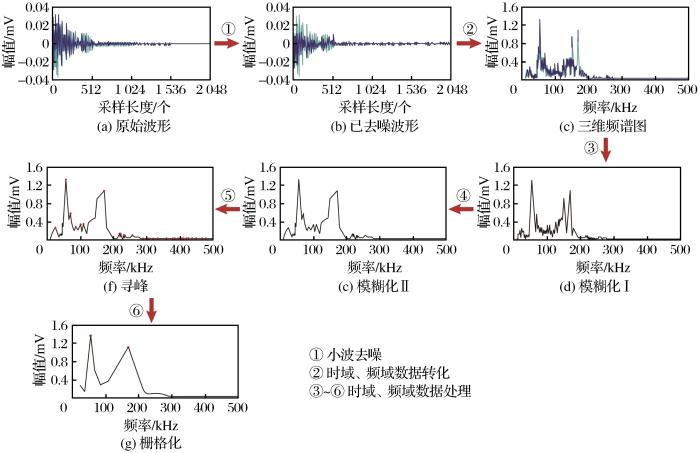
（2）试验方法及参数设置。采用纽迈MiniMR-60核磁共振仪和电液伺服岩石试验机对青砂岩岩样进行孔隙率检测及单轴压缩声发射试验。具体方法如下：首先，将3块青砂岩试样放入核磁共振仪中，通过信号接收设备将检测数据绘制成T2频谱图；其次，将2个声发射探头均匀涂抹耦合剂后用工业胶带固定于试样两侧；最后，将处理好的试样装入引伸计中，设置试验机参数为预加荷载2 kN、加载速率0.1 mm/min；最后，设置声发射参数为采样频率100 kHz，采样长度2 048个，波形门限40 dB，参数门限40 dB，前放增益40 dB。

2 青砂岩试验特征及形态劣化规律分析

2.1 孔隙特征分析

根据核磁共振原理，隙流体中的H质子受外加磁场作用会吸收电磁能，这种现象叫弛豫（Coates et al.，2007；李杰林等，2012；毛思羽等，2020）。弛豫速率可表达为

\frac{1}{T_{2}} = \frac{1}{T_{2 自由}} + ρ^{2} {(\frac{S}{V})}_{孔隙} + \frac{D (γ G T_{E})^{2}}{12}

（1）

当岩石孔隙中只有一种流体时，体积弛豫所表现出的变化要比表面弛豫慢，因此T_2自由可以忽略不计，当磁场均匀且同时采用短的 $T_{E}$ 时，扩散弛豫也可忽略，将式（1）简化为

\frac{1}{T_{2}} = ρ^{2} {(\frac{S}{V})}_{孔隙} = \frac{F_{S}}{r} ρ^{2}

（2）

式中：T_2自由为流体自由弛豫；S为孔隙表面积（cm²）；ρ²为横向表面弛豫强度（μm/ms）； $D$ 为扩散系数；γ为旋磁比［rad/（S·T）］；G为磁场梯度（G/cm）； T_E 为回波时间（ms）；F_S 为几何形状因子；r为孔隙半径（cm）。

由式（2）可知，弛豫速率取决于孔隙的表面与体积之比（S/V）（张昌达等，2006）。由此说明 $T_{2}$ 值越小，则孔隙越小，反之， $T_{2}$ 值越大，则孔隙越大（周科平等，2012；Cai et al.，2013；毛思羽等，2020；杨明等，2021）。将0.01~10 ms划分为小孔、10~100 ms划分为中孔、100~1 000 ms划分为大孔，由此可知 $r$ 越大，则 $T_{2}$ 越大，根据核磁测试原理绘制青砂岩岩样的 $T_{2}$ 频谱图，如图4所示。

图4

图4 青砂岩试样T₂频谱图

Fig.4 T₂ spectrum of green sandstone rock sample

由图4可知，青砂岩的T₂分布区间大致位于10^-1~10³ms之间，呈双峰结构，第一谱峰位于1^{ms附近，为小孔；第二谱峰位于10~10²ms之间，为中孔，即青砂岩试样为小孔和中孔并存。由曲线分布情况可知同一岩性的相同试样孔隙分布规律及大小相似，由于第一谱峰高于第二谱峰，可确定青砂岩的3块试样均以小孔为主，局部存在部分中孔。}

2.2 QSY试样试验结果特征分析

（1）应力—时间特征分析。根据QSY（青砂岩）孔隙特征，同一岩石所取试样的孔隙率存在类同（表2），故在篇幅一定的情况下，选择QSY₁进行分析，下文均以QSY命名。

表2 青砂岩孔隙率测试结果

Table 2 Porosity test results of green sandstone

试样编号	体积/cm³	信号量	孔隙率/%
QSY₁	190.71	1 867	3.12
QSY₂	190.57	1 877	3.24
QSY₃	190.98	1 914	3.71

轴向应力—时间曲线作为试样在外荷载下直观的分析曲线，能够很好地揭示岩石受力破坏机制和规律，如图5所示，其特征分布如下：

图5

图5 青砂岩单轴压缩轴向应力—时间曲线

Fig.5 Axial stress-time curve of green sandstone under uniaxial compression

①依据张安斌等（2017）和陈国庆等（2018）对外荷载下砂岩全应力—时间曲线划分依据，可将青砂岩受载过程划分为3个阶段：阶段Ⅰ（压密阶段，OA段），应力缓慢增加，曲线朝上凹，青砂岩试样内部孔隙和微裂隙逐渐被压缩闭合产生非线性变形；阶段Ⅱ（弹性变形阶段，AB段），曲线近似直线，局部存在少许上凹，属线性关系；阶段Ⅲ（塑性变形阶段，BC段），曲线由直线状形成突变，发生偏离。

②吴贤振等（2015）提出岩石变形破坏类型可划分为脆性破坏、脆—延性破坏和延性破坏3种，其中脆性破坏应力达到峰值后会直接失去承载。由应力—时间曲线的阶段Ⅲ（BC段）可以看出，当试样的轴向应力达到峰值时会失去承载，因此可以确定青砂岩的破坏类型为脆性破坏，3块试样的轴向应力强度分别为48.5，47.7，49.8 MPa，平均值为48.7 MPa，均值强度与QSY₁较为接近，如表3所示。

表3 青砂岩试样轴向应力试验结果

Table 3 Axial stress test results of green sandstone samples

岩性	试样编号	单轴抗压强度σ_c/MPa	平均值 ${\bar{σ}}_{c}$ /MPa
青砂岩（QSY）	QSY₁	48.5	48.7
	QSY₂	47.7
	QSY₃	49.8

（2）AE声发射特征信号分析。在声发射室内试验中，受外界环境影响，AE采集系统所收集的信号不是试样在外荷载下破裂的全部信号且伴有噪声。为减少噪声对试验结果的影响，需进行去噪处理，常用的去噪方法是物理去噪法，如涂抹黄油等，虽然在一定程度上能够减弱噪声的影响，但无法彻底消除。基于此，本文在前人研究（常新科，2020）的基础上，采用小波阈值去噪的软阈值方法，依据图6所示流程，按照初始设定的2 048个采样点为一个采样长度进行采集去噪处理，然后采用MATLAB软件对AE信号进行再处理，得到青砂岩时域、频域信号演化关系，如图7和图8所示。

图6

图6 AE原始波形处理流程图

Fig.6 Flow chart of AE original waveform processing

图7

图7 外荷载下青砂岩时域信号演化关系图

Fig.7 Time domain signal evolution diagram of green sandstone under external load

图8

图8 AE主频、轴向应力随时间演化特征图

Fig.8 Evolution characteristics of AE dominant frequency and axial stress with time

①AE时域变化特征分析

如图7所示，AE时域信号演化特征分布如下：

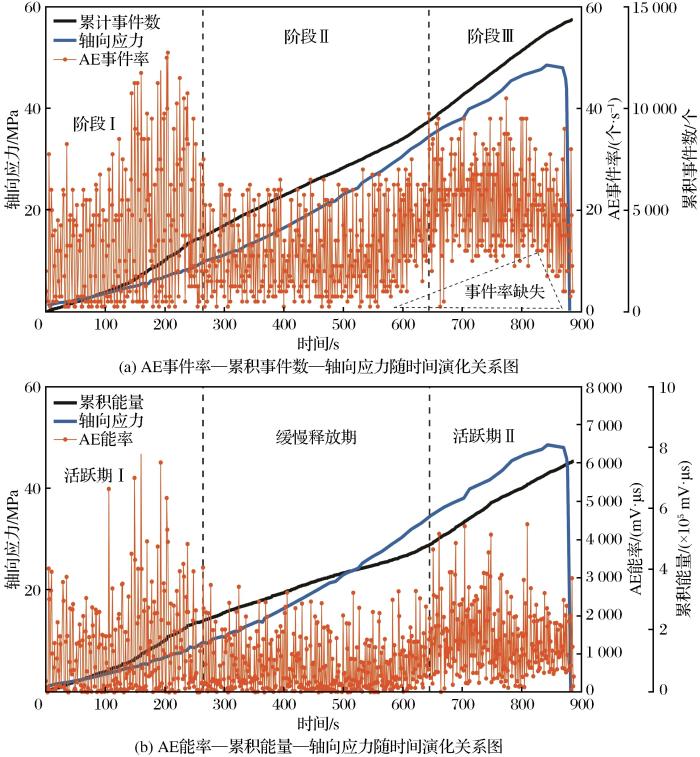
随着轴向应力的增长和下降，AE时域信号呈“上升—降低—上升”变化，上升期表现为由低事件率和低能率向高事件率和高能率发展，降低期表现则相反，AE累积事件数和累积能量随着时间和轴向应力的变化累积增长，事件率整体变化趋势呈近似倒“M”型，能率整体变化趋势呈近似“U”型。

根据青砂岩试样的应力—时间变化规律，结合李仕璋（2021）对裂纹体积应变法在岩石受力破坏中的阶段划分以及事件率和能率的变化规律，可将青砂岩的AE事件率和能率划分为3个阶段，且各阶段相互对应。具体如下：阶段Ⅰ（压密阶段），因试样内部原生孔隙和微裂隙在加载下得到压密闭合，释放部分压缩能，AE事件率和能率由低向高发展；阶段Ⅱ（弹性变形阶段），试样密实度持续增大，以吸收压缩能为主，事件率和能率均表现较为平缓，后期表现出一定的弹塑性特征；阶段Ⅲ（塑性变形阶段），在高应力作用下，试样内部原生微裂隙发生扩展，相互贯通，并释放出能量，能率和事件率上升，达到峰值应力后发生突降，试样发生破坏，此时AE累积事件数和累积能量达到最大值，分别为14 379 a和9.07×10⁵mV·μs。同时，由于岩石试样声学性能特征具有离散性，因此3块试样在3个阶段表现出的AE事件率和能率存在差异，每一阶段的事件数和能率均不同，但由于3块试样取自同一块岩石，相互之间的差异变化较小，如表4所示，后续可针对同一岩性的不同岩石进行相关分析。

表4 青砂岩试样AE信号试验结果

Table 4 AE signal test results of green sandstone samples

参数名称	青砂岩试样及试验结果
参数名称	QSY₁	QSY₂	QSY₃
阶段Ⅰ累积事件数/个	3 681	3 573	3 812
阶段Ⅰ累积能量/［（mV·μs） ·s^-1］	2.81×10⁵	2.73×10⁵	2.93×10⁵
阶段Ⅱ累积事件数/个	9 381	8 768	9 627
阶段Ⅱ累积能量/［（mV·μs）·s^-1］	5.79×10⁵	5.42×10⁵	5.91×10⁵
阶段Ⅲ累积事件数/个	14 379	13 694	15 098
阶段Ⅲ累积能量/［（mV·μs）·s^-1］	9.07×10⁵	8.46×10⁵	9.24×10⁵

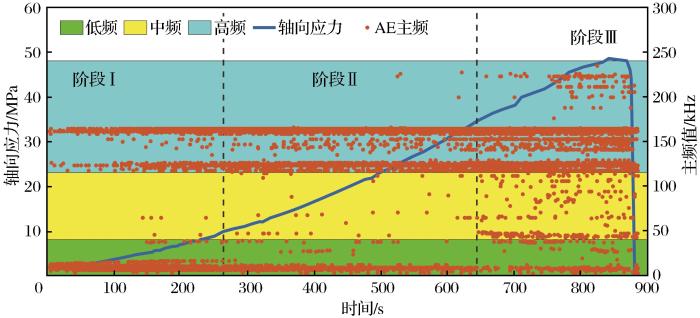
AE事件率缺失存在2个方面的原因（闫章程等，2020；常新科，2020）：原生缺陷闭合和试样破坏征兆。其中，试样破坏征兆特征表现为低水平事件率消失，中、高水平事件率交替出现，且能够维持一定时间，当失稳发生时，表现为下降趋势。青砂岩的事件率缺失处信号表现为交替上升至中、高水平，且在中、高水平内保持上下波动，不存在低事件信号，当达到峰值应力后缺失现象消失，由此可判定事件率缺失为试样破坏征兆。

②AE频域变化特征分析如图8所示。根据上文分析，也可将AE主频划分为3个阶段，结合AE主频信号高低分布特点及主频群集现象，划分为低频、中频和高频，特征分布如下：

AE主频信号主要位于低频和高频区内，中频区内的信号较少，且低频和高频信号无间断，王创业等（2020）将这种频带称为岩石破裂过程的主导频带。

AE主频信号的3个阶段：阶段Ⅰ（压密阶段），高、低频带为无间断信号，说明试样内部孔隙和原有缺陷发生压实；阶段Ⅱ（弹性变形阶段），压密结束，高、低频带连续信号宽度加大，伴有间断信号产生，且中频带有大量间断信号形成，Cai et al.（2007）将该现象称为微裂纹萌生和原生裂纹重新发育；阶段Ⅲ（塑性变形阶段），试样低频带连续信号宽度变窄、高频带宽度变宽，中、高频带伴有局部信号聚集成带现象，说明在此阶段新萌生和重新发育的微裂纹存在贯通现象，直至达到峰值应力时发生破坏，高、中、低频3个频带分别对应10~42，42~117，117~241 kHz，其余2块试样的频带分布与试样QSY₁频带分布差距较小，如表5所示。

表5 青砂岩试样AE主频试验结果

Table 5 AE dominant frequency test results of green sandstone samples

主频类型	青砂岩试样及试验结果
主频类型	QSY₁	QSY₂	QSY₃
高频/kHz	117~241	122~250	120~248
中频/kHz	42~117	44~122	44~120
低频/kHz	0~42	0~44	0~44

2.3 青砂岩受力破坏特征分析

试样在加载下的破坏方式以张拉和剪切破坏为主，此过程中会诱发大量固定形态的AE信号（刘建坡等，2015；张鹏海，2015）。常新科（2020）采用AE时序参数RA-AF值对此进行表征，其中，RA为上升时间与幅值的比值，AF为撞击计数与持续时间的比值，表达式为

R A = \frac{R i s e t i m e}{A m p l i t u d e}

（3）

A F = \frac{C o u n t s}{D u i a t i o n}

（4）

式中：RA为上升时间和幅值的比值（ms/V）；AF为撞击计数和持续时间的比值（kHz）。当AF>RA时，岩样破坏类型为张拉破坏，形成张拉裂纹；当AF<RA时，岩样破坏类型为剪切破坏，形成剪切裂纹，如图9所示，根据AE时序参数RA-AF定义，利用MATLAB软件计算后得到青砂岩试样的AE信号时序参数RA-AF分布图，如图10所示。

图9

图9 AE信号时序参数裂纹分类示意图

Fig.9 Crack classification diagram of AE signal time series parameter

图10

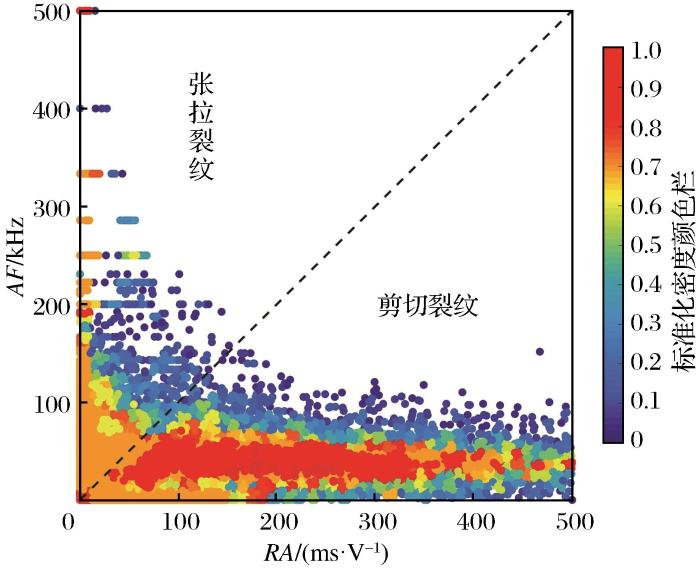
图10 AE信号时序参数RA-AF分布图

Fig.10 RA-AF distribution diagram of AE signal time series parameters

图10中0表示散点数量最为稀疏的位置（蓝色），1表示散点数量最为稠密的位置（红色）。青砂岩的RA值为0~500 ms/V，AF值为0~250 kHz；试样破坏后，位于剪切裂纹区域的红色和橘色面积占比较大，标准化密度达到0.6以上，张拉裂纹区域虽存在部分橘色和黄色，但相比蓝色占比小，也不存在红色区域，结合图11和图12可以看出青砂岩的3块试样破坏类型主要为剪切破坏，破坏方式为单斜面和双斜面剪切破坏，形成裂纹为剪切裂纹。

图11

图11 青砂岩试样破坏形态

Fig.11 Failure mode of green sandstone samples

图12

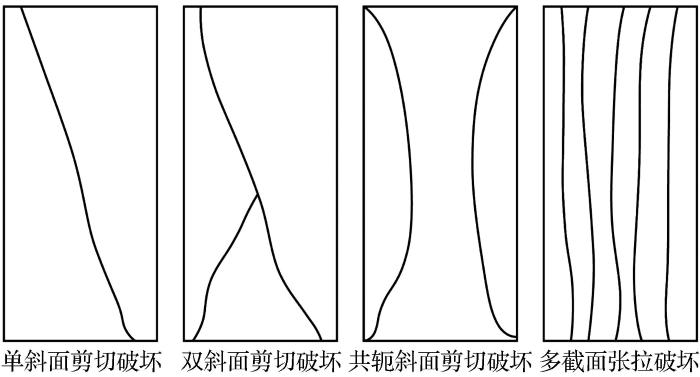
图12 试样不同破坏特征示意图

Fig.12 Schematic diagram of different failure characteristics of rock samples

3 青砂岩元胞自动机模型建立及损伤临界值确定

3.1 元胞自动机

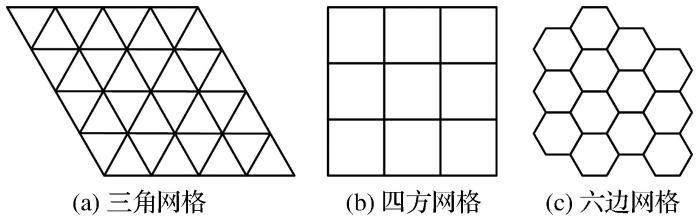
元胞自动机（Cellular Automaton，CA）是由美国著名的数学家Von Neumann提出来的，用来模拟离散动力系统内部单元之间因强烈非线性作用而导致系统自组织演化过程的一种动力学建模方法（Wolfram，1983；马志涛等，2005）。它能够对复杂系统的时空演化过程进行模拟，由元胞、元胞空间、元胞邻居和元胞规则4个部分组成，如图13所示。常见的元胞模型有三角网格、四方网格和六边网格（萨木哈尔·波拉提等，2020），如图14所示。

图13

图13 元胞自动机构成示意图

Fig.13 Schematic diagram of cellular automata composition

图14

图14 常见的元胞空间结构

Fig.14 Common cellular space structure

3.2 青砂岩元胞模型建立及损伤特征分析

近年来，相关学者在分形理论的基础上将元胞自动机引入岩石损伤研究中。损伤作为对岩石劣化程度的定量描述，其值可表示为0≤D≤1；当D=0时试样处于无损状态；当0<D<1时，试样由无损向损伤劣化转变；当D=1时，试样完全损伤。试样受载过程中内部颗粒会发生随机破坏，破坏后的颗粒对周边颗粒形成新的作用力，诱发周围其他颗粒也发生破坏，依此类推，直至发生破裂，这种现象与元胞自动机中微元单元破坏较为一致。在上述基础上，结合青砂岩结构特征、损伤理论和Weibull分布函数建立Moore型四方网格的元胞模型，具体为：首先，假定试样的损伤发生在某个截面处；其次，将这个截面进行单元划分；最后，将划分好的每个单元设为一个元胞，Moore型四方网格元胞模型如图15所示。

图15

图15 Moore型元胞邻居模型

Fig.15 Moore-type cellular neighbor model

如图15所示，建立3×3二维元胞模型，将试样截面划分为3n×3n的网格单元，假设：①建立的元胞单元受到相同作用力 $F$ （图16），当 $F$ 大于元胞承受的最大荷载时，岩样发生破坏，作用力 $F$ 继续向相邻元胞单元转移，且在转移过程中使2个相邻元胞同时发生破坏可判定此级元胞发生破坏；②试样中每个元胞单元破坏概率服从Weibull函数分布规律（张慧梅等，2014；梁辉等，2016）；③试样损伤值 $D$ 为元胞单元 $的破坏总概率 P (F)$ 。

图16

图16 元胞单元受力模型图

Fig.16 Stress model diagram of cellular unit

依据李胜林等（2017）提出的单元重整化方法构建9个单元标度的重整化Moore型元胞邻居模型，使9个1级元胞组成一个2级元胞，9个2级元胞组成一个3级元胞，依次类推，周而复始，不断重构，如图17所示。

图17

图17 元胞单元重整化示意图

Fig.17 Schematic diagram of cellular units renormalization

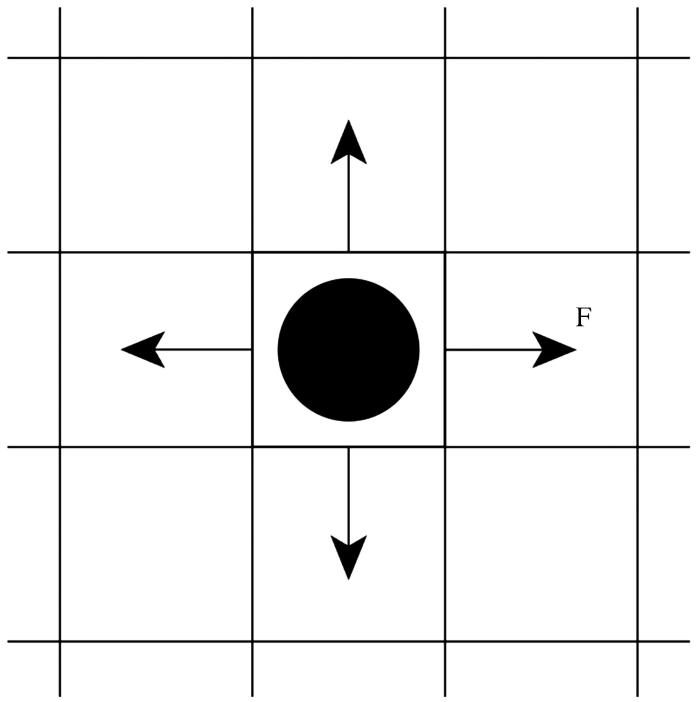
假设在力F作用下各级元胞的破坏情况分为2个部分：第一部分为元胞自身破坏概率，用P表示；第二部分为破坏元胞应力传递扩散概率，用P_m表示，则第一部分元胞不破坏的概率为1-P，由此可以确定元胞模型的破坏分类情况，如表6所示。

表6 元胞单元破坏模型分类（个）

Table 6 Classification of cellular unit destruction model

被破坏单元胞数	被破坏单元数量	未被破坏单位数量	应力扩散元胞相邻已损坏元胞数
被破坏单元胞数	被破坏单元数量	未被破坏单位数量	1	2	3	4
0	0	1	0	0	0	0
1	0	9	24	0	0	0
2	16	20	60	22	0	0
3	68	16	28	36	8	0
4	120	6	0	16	8	1
5	125	1	0	0	4	0
6	84	0	0	0	0	0
7	36	0	0	0	0	0
8	9	0	0	0	0	0
9	1	0	0	0	0	0

由表6可以得出1级元胞破坏概率的计算步骤如下：

（1）9个单元全部完好的概率可表示为

P {(F)}_{1} = {(1 - P)}^{9}

（5）

则元胞破坏概率为

P_{1} = 0

（6）

（2）9个单元中只有1个破坏的概率可表示为

P {(F)}_{2} = 9 P {(1 - P)}^{8}

（7）

扩散后被破坏的概率为

P (F_{1})_{2} = 9 P {(1 - P)}^{8} 24 P_{m}

（8）

元胞破坏的概率表示为

P_{2} = P_{1} + P (F_{1})_{2}

（9）

依此类推。

（3）9个单元中只有9个破坏的概率可表示为

P {(F)}_{10} = P^{9}

（10）

元胞破坏概率为

P_{10} = P {(F)}_{10}

（11）

通过上述计算可得出在力 $F$ 作用下，元胞破坏的总概率为

\begin{array}{l} P (F) = P_{1} + P_{2} + P_{3} + P_{4} + P_{5} + P_{6} + P_{7} + P_{8} + P_{9} + P_{10} = 68 P^{5} {(P - 1)}^{6} - 16 P^{2} {(P - 1)}^{7} - 120 P^{4} {(P - 1)}^{5} + 125 P^{5} {(P - 1)}^{4} - \\ 84 P^{6} {(P - 1)}^{3} + 36 P^{7} {(P - 1)}^{2} + P^{9} - 9 P^{8} (P - 1) + 216 P P_{m} {(P - 1)}^{8} - 12 P_{m} [120 P^{4} {(P - 1)}^{5} + 360 P^{4} P_{m} {(P - 1)}^{5}] {(P - 1)}^{4} - 1 440 P^{2} P_{m} {(P - 1)}^{7} + 2 496 P^{3} P_{m} {(P - 1)}^{6} - 360 P^{4} P_{m} {(P - 1)}^{5} \end{array}

（12）

由于岩石具有自相似和自组织性，不动点定理可适用于元胞机失效表达，即一级元胞与多级元胞的失效表达相同，则有：

P = P (F)

（13）

李胜林等（2017）假设各相邻元胞之间无相互作用，即元胞破坏后，应力不发生扩散，则有P_m = 0，结合式（12）和式（13），解得P=0，1，0.078，0.43。因为0和1为稳定的不动点，由此根据上述元胞模型求得破坏概率，可确定0.078和0.43为不稳定的不动点，加之0.078与0相差较小，可归于不动点0处，则可确定损伤0.43为不稳定的不动点，即当D>0.43时，岩石内部微裂纹受外力作用存在加速，由稳定状态向不稳定状态转变，当达到极限损伤值时（D=1）就会发生破坏。

3.3 青砂岩单轴压缩损伤演化规律分析

试样在荷载下的演化过程，其实质是裂纹的萌生、扩展和贯通，前人研究指出试样微单元强度服从Weibull函数分布规律（陈忠辉等，2002；张檑，2011；赵宏宝等，2011），即：

φ (ε) = \frac{m}{α} ε^{m - 1} e x p (- \frac{ε^{m}}{α})

（14）

式中：ε为试样受载的应变值；m为试样形状参数；α为试样的尺度参数；φ（ε）为单元损伤率。

根据文献（张檑，2011），试样变形破坏可用损伤量D表示，由此可以推出损伤变量与微单元损伤率之间的关系，即：

φ (ε) = \frac{d D}{d ε}

（15）

将式（14）与式（15）联立，可得：

D = \int_{0}^{ε} φ (x) d x = 1 - e x p (- \frac{ε^{m}}{α})

（16）

大量研究表明，试样受荷载过程中衍生的AE信号［事件数（振铃计数）］能够很好地反映损伤变量D的变化范围，此范围为0≤D≤1。若将W_m作为青砂岩的累积事件数，W则为在应力为ε时发生破坏的累积事件数，则有：

W = W_{m} \int_{0}^{ε} φ (x) d x

（17）

将式（16）与式（17）联立，可得：

\frac{W}{W_{m}} = 1 - e x p (- \frac{ε^{m}}{α})

（18）

将式（16）与式（18）进行联立，得到青砂岩的临界损伤破坏值D，可表示为

\frac{W}{W_{m}} = D

（19）

通过对W_m和W的表述，可将W_t 作为加载时长为t时的累积事件数，D_t 为对应的损伤值，可表示为

D_{t} = \frac{W_{t}}{W_{m}}

（20）

由上述可知，W_m为试样在荷载过程中的累积事件数（累积振铃计数），W为试样在应力为 $ε$ 时发生破坏的累积事件数（累积振铃计数），根据式（19）和式（20）可计算出青砂岩的临界损伤值和损伤演化过程，如图18所示。

图18

图18 青砂岩损伤演化过程

Fig.18 Damage evolution process of green sandstone

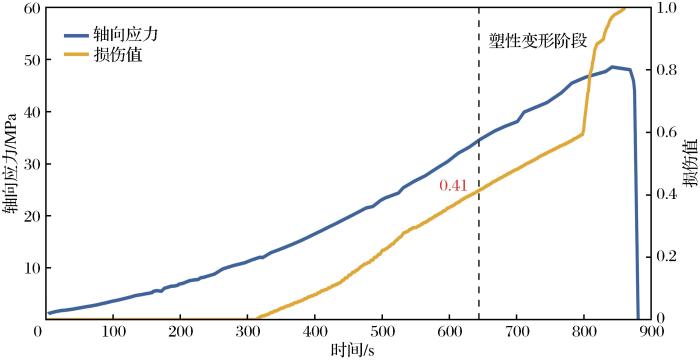
由图18可以看出，试样的损伤演化规律与应力—时间变化及AE信号变化规律相似。因此，根据裂纹体积应变法，可将损伤演化过程划分为3个阶段，分别是损伤平静阶段、损伤萌生阶段和损伤变形阶段。各阶段的变化规律分布特征如下：

损伤平静阶段：青砂岩内部孔隙和原生微缺陷处于AE信号特征的压密阶段，损伤值近乎趋近于0，沿着0轴移动，相对应力—时间和AE信号的第一阶段时间略长。

损伤萌生阶段：青砂岩内部孔隙和微缺陷的压密结束，在高应力作用下损伤值由0逐步发生变化，主要原因是受矿山生产影响，试样内部存在微缺陷，因此在弹性阶段发生了损伤演化，其间隔损伤值为0.41，未达到所建立的青砂岩元胞模型的不稳定损伤值0.43，此过程中虽然试样存在损伤变化，但稳定性较好。

损伤变形阶段：试样因弹性阶段的不可逆损伤破坏，随着荷载持续，内部原生缺陷和新生裂隙持续扩展，导致损伤值持续增大，直至损伤值达到0.599（大于0.43）时，因微裂纹扩展贯通形成大裂纹，达到峰值应力时试样发生失稳破坏，损伤值快速增长至1。

4 结论

（1）基于核磁共振原理对青砂岩3块试样进行了监测，确定了3块试样均以小孔为主，伴有部分中孔；通过应力—时间曲线变化规律可确定压缩过程中试样经历3个阶段，即OA段（压密阶段）、AB段（弹性变形阶段）和BC段（塑性变形阶段），其中第一阶段为非线性变形，第二阶段为线性变形。

（2）以小波软阈值去噪方法处理后的AE特征信号具有不同的分布特征和信息表现，事件率变化呈近似倒“M”型，能率变化呈近似“U”。由AE时序参数特征可知，试样的破坏类型划分为张拉和剪切破坏，当AF>RA值时试样表现为张拉破坏，当AF<RA值时试样表现为剪切破坏。青砂岩的RA-AF值分布范围分别为0~500 ms/V和0~250 kHz，位于剪切裂纹区的红色和橘色区域面积占比较大，标准化密度达到0.6以上，张拉裂纹区以蓝色区域为主，存在部分橘色和黄色区域，无红色区域，由RA-AF值和3块试样的破坏形态可确定青砂岩的破坏方式主要为单斜面和双斜面剪切破坏，形成的裂纹为剪切裂纹。

（3）根据岩石损伤演化的自组织现象、丛集行为及服从幂律分布特征，结合岩石结构分形和损伤理论建立青砂岩损伤二维元胞模型，归纳出青砂岩3个损伤变形阶段，即损伤平静阶段、损伤萌生阶段和损伤变形阶段。研究确定了当试样损伤值达到0.43时，试样内部微裂纹萌生和发育会加速，试样由稳定状态向不稳定状态转变。通过计算确定了试样在损伤萌生阶段的间隔损伤值为0.41，未达到0.43的不稳定损伤值，稳定性较好，直至损伤值达到0.599（大于0.43）时，在微裂纹扩展贯通形成大裂纹时，损伤加剧，试样发生失稳破坏，损伤值快速增长至1。

http://www.goldsci.ac.cn/article/2023/1005-2518/1005-2518-2023-31-3-516.shtml

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[]

Cai

， Kaiser

P K

， Morioka

，et al，2007.

FLAC/PFC coupled numerical simulation of AE in large-scale underground excavations

［J］.International Journal of Rock Mechanics and Mining Sciences，44（4）：550-564.

Cai

Y D

， Liu

D M

， Pan

Z K

，et al，2013.

Petrophysical characterization of Chinese coal cores with heat treatment by nuclear magnetic resonance

［J］.Fuel，108：292-302.

Chang

Xinke

，2021.

Multi-parameter Coupling Analysis of Acoustic Emission in Different Rock Failure

［D］.Baotou：Inner Mongolia University of Science and Technology.

Chen

Guoqing

， Zhao

Cong

， Wei

Tao

，et al，2018.

Evaluation method of brittle characteristics of rock based on full stress-strain curve and crack initiation stress

［J］.Chinese Journal of Rock Mechanics and Engineering，37（1）：591-597.

Chen

Zhonghui

， Tan

Guohuan

， Yang

Wenzhu

，2002.

Renormalization study and numerical simulation on brittle failure of rocks

［J］.Chinese Journal of Geotechnical Engineering，24（2）：184-187.

Coates G，Xiao Lizhi，Prammer M，2007.NMR Logging Principles and Application［M］.Meng Transl.Beijing：Petroleum Industry Press：36-39.

Dong

Zhikai

， Li

Haoran

， Ouyang

Zuolin

，et al，2019.

Reserch on temporal and spatial evolution characteristics of acoustic emission of marble under uniaxial compression

［J］.Chinese Journal of Underground Space and Engineering，15（Supp.2）：609-615.

Fan

L F

， Gao

J W

， Wu

Z J

，et al，2018.

An investigation of thermal effects on micro-properties of granite by X-ray CT technique

［J］.Applied Thermal Engineering，140：505-519.

Gong

Yuxin

， He

Manchao

， Wang

Zhenghong

，et al，2013.

Research on time-frequency analysis algorithm and instantaneous frequency precursors for acoustic emission data from rock failure experiment

［J］.Chinese Journal of Rock Mechanics and Engineering，32（4）：787-799.

Hongguang

， Wang

Hongwei

， Cao

Shanzhong

，et al，2012.

Experimental research on frequency characteristics of acoustic emission signals under uniaxial compression of granite

［J］.Chinese Journal of Rock Mechanics and Engineering，31（Supp.1）：2900-2905.

Kaiser

E J

，1959.

A Study of Acoustic Phenomena in Tensile Test

［D］.Munchen：Technisce Hochschule.

Jielin

， Zhou

Keping

， Zhang

Yamin

，et al，2012.

Experimental study of rock porous structure damage characteristics under condition of freezing-thawing cycles based on Nuclear magnetic resonance technology

［J］.Chinese Journal of Ro-ck Mechanics and Engineering，31（6）：1208-1214.

Shenglin

， Zhang

Qingcheng

， Wu

Shuaifeng

，et al，2017.

Theoretical study and SHPB experimental verification on the critical damage of uniform sandstone

［J］.Journal of Beijing Institute of Technology，37（8）：807-812，823.

Shizhang

，2021.

Experimental Study on the Influence of Freeze-thaw Cycles on Physical and Mechanical Properties of Sandstone

［D］.Baotou：Inner Mongolia University of Science and Technology.

X B

， Cao

W Z

， Zhou

Z L

，et al，2014.

Influence of stress path on excavation unloading response

［J］.Tunnelling and Underground Space Technology，42：237-246.

Yuanhui

， Liu

Jianpo

， Zhao

Xingdong

，et al，2009.

Study on b-value and fractal dimension of acoustic emission during rock failure process

［J］.Rock and Soil Mechanics，30（9）：2559-2563，2574.

Liang

Hui

， Zou

Ronghua

， Peng

Gang

，et al，2016.

Damage constitutive model of concrete based on Weibull statistical theory

［J］.Journal of Yangtze River Scientific Research Institute，33（2）：111-114.

Liu

Jianpo

， Liu

Zhaosheng

， Wang

Shaoquan

，et al，2015.

Analysis of acoustic emission source mechanisms for tensile and shear cracks of rock fractures

［J］.Journal of Northeastern University（Natural Science），36（11）：1624-1628.

Zhitao

， Tan

Yunliang

，2005.

Simulation study of rock failure based on MH-PCA model

［J］.Chinese Journal of Rock Mechanics and Engineering，24（15）：2704-2708.

Mao

Siyu

， Cao

Ping

， Li

Jianxiong

，et al，2020.

Fatigue damage analysis of fractured sandstone based on nuclear magnetic resonance T2 spectrum

［J］.Gold Science and Technology，28（3）：430-441.

Bolati

Samuhaer

， Zhou

Xinjie

， Hao

Ming

，et al，2020.

Discussion on evacuation model based on cellular automata

［J］.Safety and Environmental Engineering，27（5）：122-127.

Tan

Yunliang

， Zhou

Hui

， Wang

Yongjia

，et al，2001.

Physical cellular automata theory for simulating the failure evolution of mesoscopic heterogeneous materials

［J］.Journal of Physics，50（4）：704-710.

Wang

Chuangye

， Chang

Xinke

， Liu

Yilin

，et al，2020.

Spectrum evolution characteristics of acoustic emission during the rupture process of marble under uniaxial compression condition

［J］.Rock and Soil Mechanics，41（Supp.1）：51-62.

Wolfram

，1983.

Statistical mechanics of cellular automata

［J］.Reviews of Modern Physics，55（3）：601-643.

Xianzhen

， Liu

Jianwei

， Liu

Xiangxin

，et al，2015.

Study on the coupled relationship between AE accumulative ring-down count and damage constitutive model of rock

［J］.Journal of Mining and Safety Engineering，32（1）：28-41.

Xianzhen

， Liu

Xiangxin

， Liang

Zhengzhao

，et al，2012.

Experimental study of fractal dimension of AE serials of different rocks under uniaxial compression

［J］.Rock and Soil Mechanics，33（12）：3561-3569.

Yan

Zhangcheng

， Sun

Hui

， Li

Liping

，et al，2020.

Acoustic emission characteristics in dry and water-saturated limestones under uniaxial compression

［J］.Journal of Yangtze River Scientific Research Institute，37（4）：109-114，121.

Yang

Ming

， Liu

Lei

， Zhang

Xuebo

，et al，2021.

Nuclear magnetic resonance experimental study on pore structure and fluid characteristics of coal at different ranks

［J］.China Safety Science Journal，31（1）：81-88.

Yang

S Q

， Jing

H W

， Li

Y S

，et al，2011.

Experimental investigation on mechanical behavior of coarse marble under six diffe-rent loading paths

［J］.Experimental Mechanics，51：315-334.

Jie

， Liu

Xiaohui

， Hao

Qijun

，2020.

Acoustic emission characteristics and damage evolution of coal and rock under different confining pressures

［J］.Coal Geology and Exploration，48（3）：128-136.

Zhang

Anbin

， Liu

Xiangxin

， Zhang

Yanbo

，et al，2017.

Experimental research on acoustic emission characteristics of argillaceous siltstone failure under different moisture contents

［J］.Chinese Journal of Underground Space and Engineering，13（3）：51-59.

Zhang

Changda

， Pan

Yuling

，2006.

Some views on petrophysical interpretation of SNMR date

［J］.Chinese Journal of Engineering Geophysics，3（1）：1-8.

Zhang

Dongming

， Bai

Xin

， Yin

Guangzhi

，et al，2018.

Analysis of acoustic emission parameters and energy dissipation characteristics and damage evolution of bedding rock failure process under uniaxial compression

［J］.Journal of China Coal Society，43（3）：646-656．

Zhang

Huimei

， Lei

Lina

， Yang

Gengshe

，2014.

Research on rock statistical damage model and determination of parameters

［J］.Journal of Hunan University of Science and Technology（Natural Science Edition），29（3）：29-32.

Zhang

， Li

Y W

， Che

M G

，et al，2018.

Energy-based brittleness index and acoustic emission characteristics of anisotropic coal under triaxial stress condition

［J］.Rock Mechanics and Rock Engineering，51（11）：3343-3360.

Zhang

， Peng

W H

， Liu

F Y

，et al，2016.

Monitoring rock failure processes using the Hilbert-Huang transform of acoustic emission signals

［J］.Rock Mechanics and Rock Engineering，49（2）：427-442.

Zhang

Lei

，2011.

The Study on the Whole Process of Concrete Uniaxial Load by Acoustic Emission Experimental

［D］.Beijing：China University of Geosciences（Beijing）.

Zhang

Penghai

，2015.

Study on Precursory Law Prior to Rock Failure Based on Acoustic Emission Time Order

［D］.Shenyang：Northeastern University.

Zhang

Yanbo

， Zhang

Hang

， Liang

Peng

，et al，2019.

Experimental research on time-frequency characteristics of AE P-wave and S-wave of granite under failure process

［J］.Chinese Journal of Rock Mechanics and Engineering，38（Supp.2）：3554-3564.

Zhao

Hongbao

， Yin

Guangzhi

，2011.

Study of acoustic emission characteristics and damage equation of coal containing gas

［J］.Rock and Soil Mechanics，32（3）：667-671.

Zhao

Hongbao

， Yin

Guangzhi

，2011.

Study of acoustic emission characteristics and damage equation of coal containing gas

［J］.Rock and Soil Mechanics，32（3）：29-32.

Zhou

Keping

， Li

Jielin

， Xu

Yujuan

，et al，2012.

Experimental study on nuclear magnetic resonance characteristics of rock under freeze-thaw cycles

［J］.Chinese Journal of Rock Mechanics and Engineering，31（4）：731-737.

Zhou

， Wu

Shunchuan

， Xu

Xueliang

，et al，2013.

Particle flow analysis of acoustic emission characteristics during rock fracture

［J］.Chinese Journal of Rock Mechanics and Engineering，32（5）：951-959.

Zuo

Jianping

， Pei

Jianliang

， Liu

Jianfeng

，et al，2011.

Investigation on acoustic emission behavior and its time-space evolution mechanism in failure process of coal-rock combined body

［J］.Chinese Journal of Rock Mechanics and Engineering，30（8）：1564-1570.

常新科

，2020.

不同岩石破裂声发射多参量耦合分析

［D］.包头：内蒙古科技大学.

[本文引用: 3]

陈国庆，赵聪，魏涛，等，2018.

基于全应力—应变曲线及起裂应力的岩石脆性特征评价方法

［J］.岩石力学与工程学报，37（1）：591-597.

陈忠辉，谭国焕，杨文柱，2002.

岩石脆性破裂的重正化研究及数值模拟

［J］.岩土工程学报，24（2）：184-187.

Coates G，肖立志，Prammer M，2007.核磁共振测井原理与应用［M］.孟繁萤译.北京：石油工业出版社：36-39.

董志凯，李浩然，欧阳作林，等，2019.

单轴荷载下大理岩声发射时空演化特征研究

［J］.地下空间与工程学报，15（增2）：609-615.

宫宇新，何满潮，汪政红，等，2013.

岩石破坏声发射时频分析算法与瞬时频率前兆研究

［J］.岩石力学与工程学报，32（4）：787-799.

纪洪广，王宏伟，曹善忠，等，2012.

花岗岩单轴受压条件下声发射信号频率特征试验研究

［J］.岩石力学与工程学报，31（增1）：2900-2905.

李杰林，周科平，张亚民，等，2012.

基于核磁共振技术的岩石孔隙结构冻融损伤试验研究

［J］.岩石力学与工程学报，31（6）：1208-1214.

李胜林，张青成，吴帅峰，等，2017.

均质砂岩损伤临界值的研究及SHPB试验验证

［J］.北京理工大学学报，37（8）：807-812，823.

李仕璋

，2021.

冻融循环对砂岩物理力学影响的试验研究

［D］.包头：内蒙古科技大学.

李元辉，刘建坡，赵兴东，等，2009.

岩石破裂过程中的声发射 b值及分形特征研究

［J］.岩土力学，30（9）：2559-2563，2574.

梁辉，邹荣华，彭刚，等，2016.

基于Weibull统计理论的混凝土率型损伤本构模型研究

［J］.长江科学院院报，33（2）：111-114.

刘建坡，刘召胜，王少泉，等，2015.

岩石张拉及剪切破裂声发射震源机制分析

［J］.东北大学学报（自然科学版），36（11）：1624-1628.

马志涛，谭云亮，2005.

岩石破坏演化细观非均质物理元胞自动机模拟研究

［J］.岩石力学与工程学报，24（15）：2704-2708.

毛思羽，曹平，李建雄，等，2020.

基于核磁共振T2谱图的裂隙砂岩疲劳损伤分析

［J］.黄金科学技术，28（3）：430-441.

萨木哈尔·波拉提，邹馨捷，郝明，等，2020.

基于元胞自动机的人员疏散模型探讨

［J］.安全与环境工程，27（5）：122-127.

谭云亮，周辉，王泳嘉，等，2001.

模拟细观非均质材料破坏演化的物理元胞自动机理论

［J］.物理学报，50（4）：704-710.

王创业，常新科，刘沂琳，等，2020.

单轴压缩条件下大理岩破裂过程声发射频谱演化特征实验研究

［J］.岩土力学，41（增1）：51-62.

吴贤振，刘建伟，刘祥鑫，等，2015.

岩石声发射振铃累计计数与损伤本构模型的耦合关系探究

［J］.采矿与安全工程学报，32（1）：28-41.

吴贤振，刘祥鑫，梁正召，等，2012.

不同岩石破裂全过程的声发射序列分形特征试验研究

［J］.岩土力学，33（12）：3561-3569.

闫章程，孙辉，李利平，等，2020.

灰岩单轴压缩过程中干燥与饱水状态对声发射特征的影响

［J］.长江科学院院报，37（4）：109-114，121.

杨明，柳磊，张学博，等，2021.

不同阶煤孔隙结构与流体特性的核磁共振试验研究

［J］.中国安全科学学报，31（1）：81-88.

余洁，刘晓辉，郝齐钧，2020.

不同围压下煤岩声发射基本特性及损伤演化

［J］.煤田地质与勘探，48（3）：128-136.

张安斌，刘祥鑫，张艳博，等，2017.

不同含水率泥质粉砂岩破裂声发射特性试验研究

［J］.地下空间与工程学报，13（3）：51-59.

张昌达，潘玉玲，2006.

关于地面核磁共振方法资料岩石物理学解释的一些见解

［J］.工程地球物理学报，3（1）：1-8.

张东明，白鑫，尹光志，等，2018.

含层理岩石单轴损伤破坏声发射参数及能量耗散规律

［J］.煤炭学报，43（3）：646-656.

张慧梅，雷利娜，杨更社，2014.

基于Weibull统计分布的岩石损伤模型

［J］.湖南科技大学学报（自然科学版），29（3）：29-32.

张檑

，2011.

混凝土单向受载全过程的声发射试验研究

［D］.北京：中国地质大学（北京）.

张鹏海

，2015.

基于声发射时序特征的岩石破裂前兆规律研究

［D］.沈阳：东北大学.

张艳博，张行，梁鹏，等，2019.

花岗岩破裂过程声发射横、纵波时频特征实验研究

［J］.岩石力学与工程学报，38（增2）：3554-3564.

赵宏宝，尹光志，2011.

含瓦斯煤声发射特性试验及损伤方程研究

［J］.岩土力学，32（3）：29-32.

赵洪宝，尹光志，2011.

含瓦斯煤声发射特性试验及损伤方程研究

［J］.岩土力学，32（3）：667-671.

周科平，李杰林，许玉娟，等，2012.

冻融循环条件下岩石核磁共振特性的试验研究

［J］.岩石力学与工程学报，31（4）：731-737.

周喻，吴顺川，徐学良，等，2013.

岩石破裂过程中声发射特性的颗粒流分析

［J］.岩石力学与工程学报，32（5）：951-959.

左建平，裴建良，刘建锋，等，2011.

煤岩体破裂过程中声发射行为及时空演化机制

［J］.岩石力学与工程学报，30（8）：1564-1570.