2022年3月22日,国家发展和改革委员会、国家能源局印发《“十四五”现代能源体系规划》,对核电发展作出了具体部署,2025年我国在运核电装机将达到7 000万千瓦,反映出我国核电的发展空间和潜力巨大。伴随着核电站的运行,产生的放射性核废料也在逐年增多。《核安全与放射性污染防治“十三五”规划及2025年远景目标》明确指出要加快高放废物处置研究,推进开展工程屏障等工艺技术研究。目前常用的高放射性核废料的处理方法是深埋地质封存,主要依据多重屏障的防护概念(Sellin et al.,2013),按照功能区分可细分为3个屏障:一是储罐屏障,用来长久安全存储高放射性核废料固化物;二是工程屏障,包括储罐以及以储罐为中心的人工结构物,如膨润土+围岩;三是地质屏障,在工程屏障之外,依靠深地层形成的一道天然屏障。
对于工程屏障外层已开展诸多研究(Wang,2010;Metz et al.,2012;Nasir et al.,2017;侯会明等,2019;Hennig et al.,2020;许迅,2021;赵艺伟等,2021),主要集中在选址、核素近场迁移和近场热流固耦合模拟等方面,对储罐本身的研究则较少。与前2种屏障相比,储罐屏障是直接隔离高放射性核废料使其不接触生物圈的核心屏障,储罐的静动力稳定性尤为重要,目前国内研究主要集中在金属储罐的化学稳定性。储罐需要超长期服役,地下环境复杂,且一旦封存将很难对其进行二次处理,因此储罐需要具有超长期耐久性。地下物理化学环境相对复杂、核废料持续放热等因素(Börgesson et al.,2001;许韬,2019),使金属在上述环境中容易腐蚀(Björkbacka et al.,2013;Soroka et al.,2021)。鉴于此,很多国家的金属储罐每隔几百年就要取出更换,但目前的技术尚难以保证金属储罐在取出来之前不遭受损坏。
金属储罐采取特殊工艺防护层,材料用量大且造价高,不利于核废料大规模处置。通过大量调研对比,碳化硅陶瓷(固态烧结)在众多材料中脱颖而出,其具有优异的化学稳定性,表1列出了碳化硅陶瓷的部分化学性质。Onofrei et al.(1984)研究了几种高放核废料陶瓷储罐的漏气特性,发现所测试陶瓷储罐的漏气率很低,且漏气率随时间的延长而逐渐降低;Haslam et al.(2005)对核废料储罐的陶瓷覆盖层在90 ℃地下水中的抗腐蚀性能进行了试验研究,计算结果显示在腐蚀作用下氧化铝覆盖层微裂纹的出现时间大于6 000年;Lee et al.(2018)将碳化硅储罐包裹在膨润土中,在70 ℃地下水中进行了3年的抗腐蚀性能试验,结果显示碳化硅储罐没有任何变化,认为碳化硅储罐可作为碳钢的替代材料;McEachern et al.(2012)计算了碳化锆和碳化硅防护层在高放核废料直接地质封存场景下的使用寿命,半定量计算预测出百万年内的破损失效概率低于万分之一。上述数据和研究均证实碳化硅陶瓷储罐具有卓越的性能,能够长期抵御地下特殊环境中的辐射侵蚀和(电)化学腐蚀。因此,有必要对高放核废料碳化硅储罐开展相关研究,进一步丰富和拓展高放核废料处置领域的相关研究与技术储备。
| 化学条件 | 化学性质 |
|---|---|
| 惰性气体,还原氛围 | 2 320 °C以下稳定 |
| 氧化氛围 | 1 000 °C 以上形成二氧化硅层,1 650 °C以下稳定 |
| 氢气 | 1 430 °C以下稳定,1 430 °C 以上重侵蚀 |
| 水蒸气 | 1 150 °C以下稳定,1 150 °C 以上少量反应 |
| 盐酸、硫酸、氢氟酸 | 煮沸不受侵蚀 |
| 浓磷酸 | 230 °C以上出现侵蚀 |
| 熔融氢氧化钠和氢氧化钾 | 500 °C以上重侵蚀 |
| 熔融碳酸钠 | 900 °C以上重侵蚀 |
虽然碳化硅的化学稳定性较高,但陶瓷往往是脆性材料,碳化硅陶瓷制成的储罐在静动力荷载作用下可能存在承载力不足的问题。因此,采取室内试验与数值计算相结合的手段,首先通过室内试验研究碳化硅的抗拉强度特征,在此基础上开展大量的数值模拟计算,对高放核废料储罐在运输、安装和深埋运行过程中的稳定性进行研究,重点研究储罐在典型静动力场景下的基本受力特征、主要影响因素以及能否产生拉伸破坏等(即拉应力超过抗拉强度的Ⅰ型断裂)。其次,为了更加真实地反映岩石撞击储罐发生破碎的过程,采用离散单元法,研究了岩块间接触参数对岩石单轴抗压强度的影响,并开展了大量的岩石撞击数值模拟试验,研究岩石撞击破碎过程、最大拉应力变化规律、岩块间接触参数与岩块体积比对撞击作用的影响。最后,对设置与不设置缓冲层的储罐进行了对比研究。
1 碳化硅抗拉强度试验与模拟研究
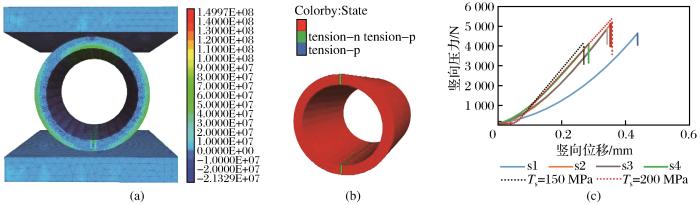
抗拉强度可能是制约碳化硅陶瓷用作高放核废料储罐的关键因素,但是由于碳化硅的抗压强度和硬度远高于绝大多数试验器材的材料(合金、钢等),使得传统的抗拉强度试验操作难度较大,同时考虑到储罐在地下的极端工况,专门设计了碳化硅空心圆柱压缩试验,借此测出碳化硅的抗拉强度,同时探究极端工况下碳化硅储罐的破坏机理,碳化硅空心圆柱的长度为5 cm,内外径分别是2 cm和2.5 cm,试验示意图如图1(a)所示。试验采用2个平板进行压缩,直至碳化硅空心圆柱的内径开始出现拉伸破坏,并最终导致整个试件的脆性破坏。为了验证数值计算的准确性,基于碳化硅的物理力学参数,建立了相应的数值计算模型,如图1(b)所示,其中实线为实验室结果,虚线为数值计算结果,碳化硅采用摩尔—库伦拉应变软化本构模型,其他参数见表2。显然,在经历了初期的应力调整后,碳化硅显示出理想线弹性的应力—应变规律,当达到一定荷载后显示出明显的脆性破坏。破坏荷载P的解析解可表示为
式中:P为破坏荷载;R为外半径长;σθ 为抗拉强度;ρ为空心圆柱的内外半径长之比;1/Z1为外部的点荷载作用下实心圆柱的破坏荷载系数,1/Z2为内部的边界荷载作用下空心圆柱的破坏荷载系数。由于计算公式比较复杂,考虑简洁性,将公式中较长的部分进行了单独命名:式(4)~
图1
图1
碳化硅空心圆柱压缩试验
(a)空心圆柱上下两端最小主应力(Pa)(拉为正)在接近抗拉强度150 MPa时发生破坏(对应图1c黑色虚线);(b)空心圆柱在上下侧发生拉伸破坏,红色图例代表未发生拉伸破坏,绿色图例代表已发生且仍在发生拉伸破坏,蓝色图例代表已发生拉伸破坏;(c)碳化硅空心圆柱压缩试验的位移—荷载曲线,实线为试验结果,虚线分别为不同抗拉强度下的数值模拟结果
Fig.1
Compression test of SiC hollow cylinder
表2 碳化硅模型参数
Table 2
| 参数 | 数值 | 参数 | 数值 |
|---|---|---|---|
| 内摩擦角φ/(°) | 40 | 剪胀角f/ (°) | 0 |
| 抗拉强度Ts/MPa | 150~200 | 弹性模量E/GPa | 415 |
| 密度ρ/(kg·cm-3) | 3.1 | 泊松比µ | 0.15 |
| 黏聚力C/GPa | 4 |
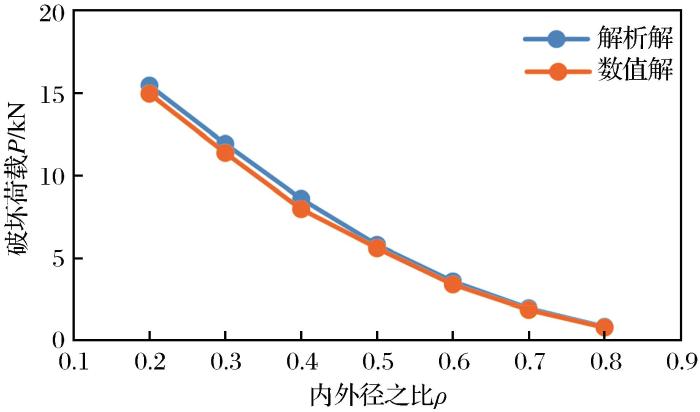
为了模拟碳化硅的脆性破坏,数值计算采用拉应力截断模型,一旦单元的拉应力超过抗拉强度,出现很小的塑性应变就会导致材料的承载力直接下降为0,其中黏聚力C根据Lee et al.(2004)基于SiC-N陶瓷的试验数据推导出来,在试验中测得的单轴抗压强度高达3 800 MPa。根据图1(a),黑色和红色虚线分别是假定碳化硅抗拉强度为150 MPa和200 MPa时的计算结果曲线,当空心圆柱上下端最小主应力接近或超过碳化硅的抗拉强度时[图1(c)],材料出现拉伸破坏[图1(b)]且压力—位移曲线出现转折点。在抗拉强度为150 MPa和200 MPa的条件下,模拟计算的曲线、峰值分别与试验结果的上下限(即绿色曲线和棕色曲线)较为相近,因此估计试验用碳化硅的抗拉强度在150~200 MPa之间,该结果与通过解析计算的结果基本一致。从安全角度来考虑,选择150 MPa作为碳化硅的抗拉强度。图2对比了空心圆柱(外径为2.5 cm,长度为5 cm)在不同内外径比条件下压缩试验破坏荷载的数值模拟结果与解析解,显然数值模拟在多种内外径比条件下均能给出较准确的解。
图2
图2
破坏荷载的数值解与解析解
(R=2.5 cm,Ts=150 MPa)
Fig.2
Analytical and numerical solutions for failure load(R=2.5 cm,Ts=150 MPa)
2 碳化硅储罐静动力荷载作用响应分析
2.1 基本理论
采取数值模拟方法研究潜在风险场景下碳化硅储罐的动静力响应。对运输、安装和运行3个场景可能发生的风险类型进行了分类,包括静力荷载和动力荷载。(1)静力荷载:运行阶段,承受较高的竖向地应力、较高的水平与竖向地应力之比(1~3);(2)动力荷载:运输工程中的自由掉落、安装过程中的洞顶岩石撞击。
通常情况下,碳化硅储罐与安装基座采用线弹性模型,岩石则分别考虑线弹性连续介质模型和线弹性非连续介质模型(离散元模型),采用离散元模型是为了更真实地考虑岩石撞击过程中的断裂破坏(Itasca Cousulting Group,2016)。动力分析在基座底部设置吸收边界,但是由于数据缺乏而不考虑阻尼的影响。储罐与岩石和地面的接触刚度采用最大应力法,即引起的储罐应力出现最大稳定值时所对应的接触刚度,同时避免穿透。
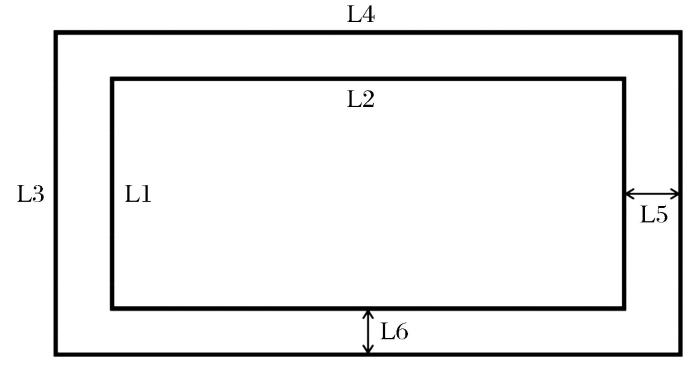
图3
表3 储罐几何参数
Table 3
| 储罐类型 | L1 | L2 | L3 | L4 | L5 | L6 |
|---|---|---|---|---|---|---|
| 62 | 305 | 92 | 335 | 15 | 15 | |
| 102 | 510 | 142 | 550 | 20 | 20 | |
| 固化核废料/V储罐 | 450 | 1 350 | 500 | 1 400 | 25 | 25 |
表4 数值模拟计算的材料基本参数
Table 4
| 材料 | 密度/ (kg·m-3) | 弹性模量E/GPa | 泊松比µ |
|---|---|---|---|
| 碳化硅 | 3 100 | 415 | 0.150 |
| 缓冲层 | 900 | 0.008 | 0.333 |
| 防护层 | 2 000 | 1.350 | 0.270 |
| 基座 | 2 500 | 70 | 0.210 |
| 岩石 | 2 500 | 47 | 0.300 |
表5 数值模拟计算的岩块间接触参数
Table 5
| 岩石 | 法向接触刚度 /(TPa·m-1) | 切向接触刚度 /(TPa·m-1) | 接触间黏 聚力/MPa | 接触抗拉 强度/MPa | 接触内摩 擦角/(°) | 残余接触黏 聚力/MPa | 残余接触抗拉 强度/MPa | 残余接触内摩 擦角/(°) |
|---|---|---|---|---|---|---|---|---|
| R1 | 75.00 | 25.00 | 40 | 10 | 0 | 0 | 0 | 27 |
| R2 | 43.20 | 4.32 | 15 | 4 | 0 | 0 | 0 | 27 |
2.2 静力荷载分析
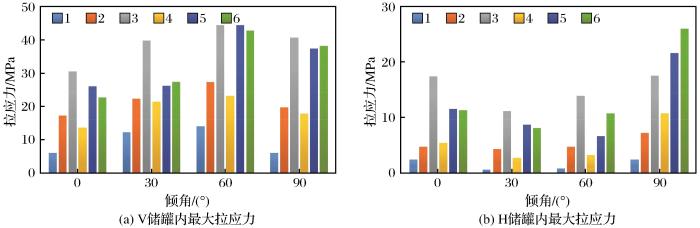
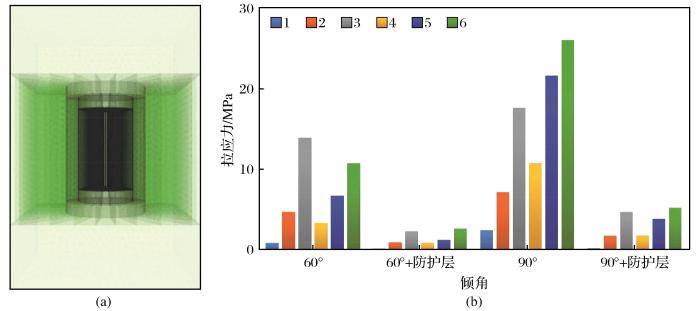
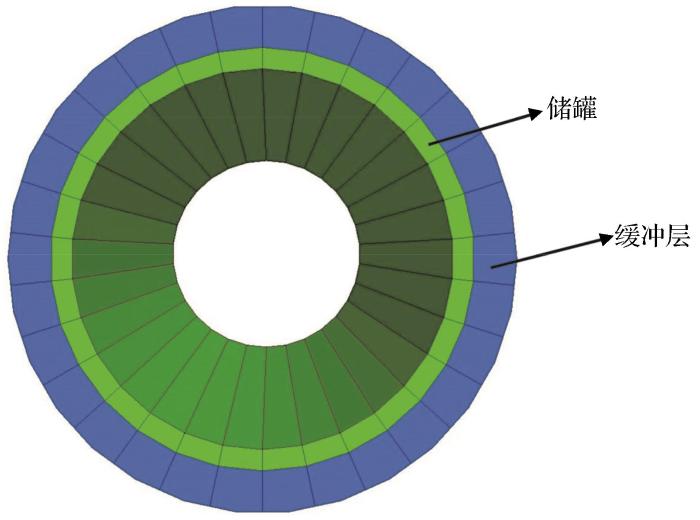
首先考虑不设置工程屏障而直接将储罐掩埋包裹在岩石中的工况。对H和V储罐进行了埋深为400 m、不同水平与竖向地应力比(表6)和不同倾角(储罐长轴线与竖直方向的夹角)条件下的数值计算。由图4可知,在相同埋深条件下,水平与竖向地应力比越大,储罐所产生的最大拉应力也越大,同时对储罐的倾角也有较大的影响,但是规律不明显。显然,在考虑到所有计算工况下,当埋深为400 m时,包裹在岩石中的储罐在未采取任何防护措施的工况下,产生的最大拉应力未超过50 MPa,远小于碳化硅150 MPa的抗拉强度值。由于计算采用纯弹性模型,意味着在水平与竖向同时扩大3倍(即埋深为1 200 m,水平与竖向地应力比为3)的情况下,储罐内部产生的拉应力不会超过150 MPa。由图5可以看出,最大拉应力主要集中在空心圆柱的两端,由图4可以看出,相同工况下V储罐的拉应力高于H储罐,其原因是二者的厚度与长度之比(0.018∶0.045)、内外径之比(0.90∶0.67)不同。对设置与未设置防护层H储罐的最大拉应力进行了对比,其中防护层厚度为200 mm。设置防护层的多层屏障系统及其最大拉应力结果如图6所示,可以看出设置防护层能够大幅降低储罐内部的拉应力。
表6 不同地应力与地应力比组合
Table 6
| 荷载 | X/MPa | Y/MPa | Z/MPa | (X/Z) |
|---|---|---|---|---|
| 1 | 10 | 10 | 10 | 1 |
| 2 | 20 | 10 | 10 | 2 |
| 3 | 30 | 10 | 10 | 3 |
| 4 | 20 | 20 | 10 | 2 |
| 5 | 30 | 20 | 10 | 3 |
| 6 | 30 | 30 | 10 | 3 |
图4
图4
不同倾角和地应力条件下储罐内的最大拉应力
Fig.4
Maximum tensile stress in canister under different inclination angle and ground stress conditions
图5
图5
储罐的应力分布
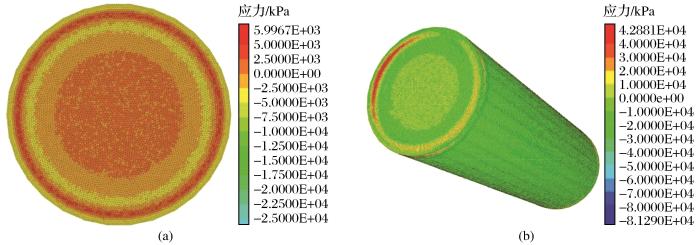
(a)V储罐,X、Y、Z方向的地应力组合为(10 MPa,10 MPa,10 MPa),倾角为90°;
(b)H储罐,X、Y、Z方向的地应力组合为(30 MPa,30 MPa,10 MPa),倾角为60°
Fig.5
Stress distribution of canister
图6
图6
多层屏障系统与防护层对最大拉应力的影响
(a)多层屏障系统(外:围岩;中:防护层;内:储罐);(b)设置与不设置防护层条件下的最大拉应力注:图例中数字代表X、Y、Z方向地应力组合,依次为:1-(10 MPa,10 MPa,10 MPa);2-(20 MPa,10 MPa,10 MPa);3-(30 MPa,10 MPa,
Fig.6
Multi-barrier system and influence of buffer layer on the maximum tensile stress
10 MPa);4-(20 MPa,20 MPa,10 MPa);5-(30 MPa,20 MPa,10 MPa);6-(30 MPa,30 MPa,10 MPa)
2.3 动力荷载分析
(1)自由跌落
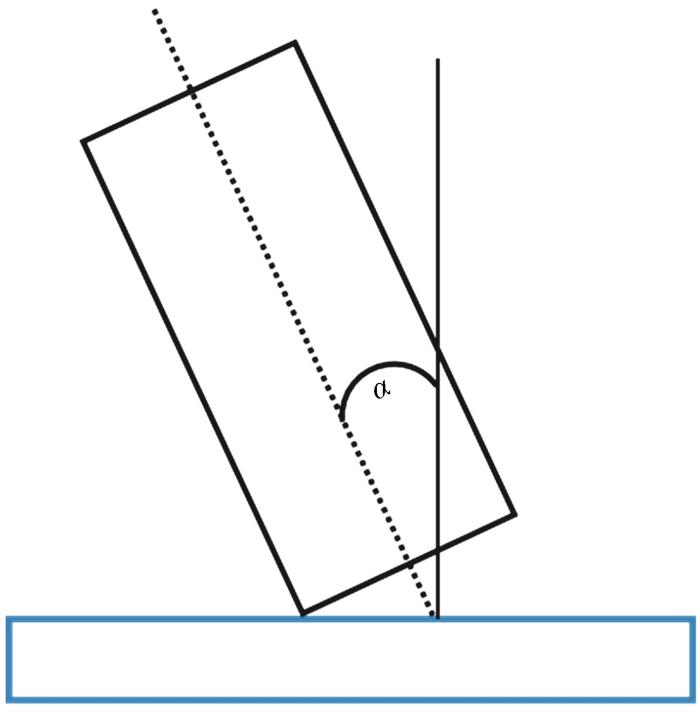
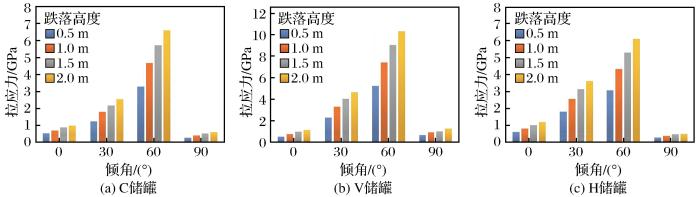
自由跌落设置了0.5,1.0,1.5,2.0 m共4个高度(高度为储罐最低点离地面的高度),长轴线与竖直方向的倾角α分别是0°,30°,60°,90°(图7),采用线弹性模型。图8为不同跌落高度与倾角条件下储罐所产生的最大拉应力统计结果,显然跌落高度越大所产生的拉应力也越大。在跌落倾角为0°和90°时所产生的拉应力明显小于30°和60°时所产生的拉应力,其中跌落倾角为90°时所产生的拉应力最小。跌落倾角对拉应力产生显著影响,主要是因为不同跌落倾角下储罐—地面的接触形式或接触面积不同,拉应力在点—面接触条件下最大(跌落倾角为30°和60°时接触面积最小),线—面接触次之(跌落倾角为0°),面—面接触最小(跌落倾角为90°时接触面积最大)。
图7
图8
图8
不同跌落高度和倾角条件下储罐内部的最大拉应力
Fig.8
Maximum tensile stress inside canister under different falling height and inclination angle conditions
但是,在所有工况下,储罐均出现了远超抗拉强度的拉应力,意味着储罐会发生破坏。为了应对这种危险场景,在储罐四周包裹了一个缓冲层,以V储罐为例,如图9所示,其中缓冲层的厚度为5 cm。在设置了缓冲层后,最大拉应力由1.1 GPa下降至0.147 GPa,从受力角度来说缓冲效果较好。
图9
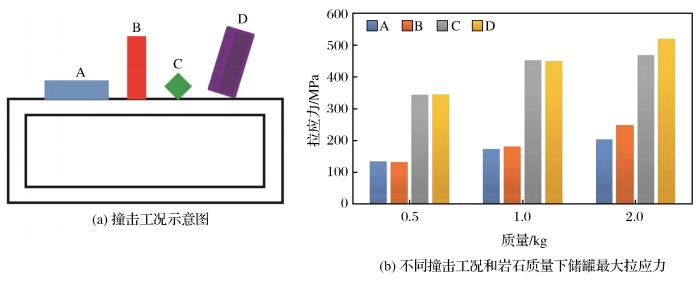
(2)岩石撞击
图10
图10
不同撞击工况和岩石质量条件下储罐最大拉应力
Fig.10
Maximum tensile stress of canister under different impact conditions and rock mass weights
即使是很小的岩石块也能在储罐内部产生接近或超过抗拉强度的拉应力,这是因为岩石是基于线弹性连续介质假设,这种假设不考虑岩石自身的破碎,与实际工况并不完全一致。在撞击过程中,接触点附近撞击应力迅速增加,接触点附近岩石和储罐的瞬时应力是同一量级,岩块可能会先出现破坏(因为一般岩石的抗拉强度和抗压强度均低于碳化硅的抗拉强度150 MPa),因此需要考虑岩石破碎,才能更准确地评价岩石的撞击作用。
图11
图11
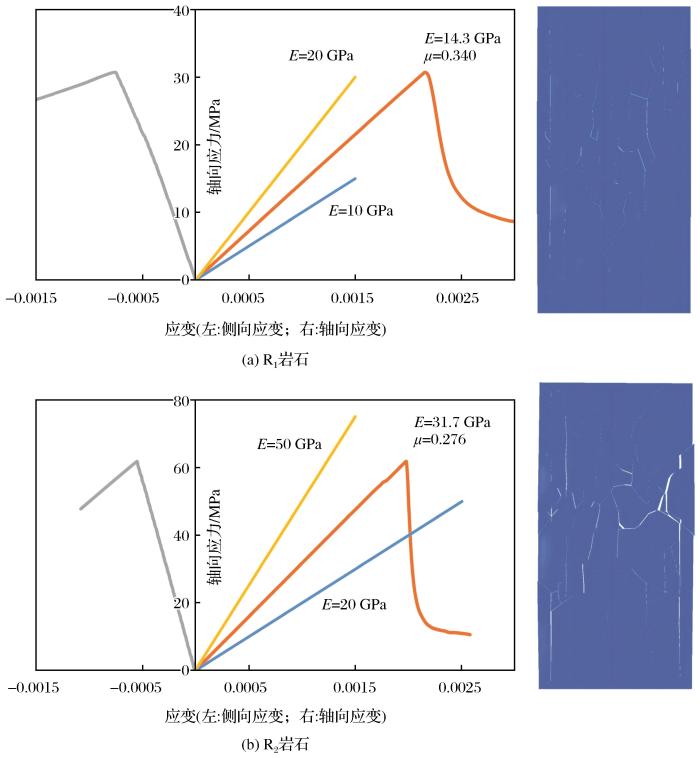
离散元模拟的单轴抗压强度应力—应变曲线与相应的岩石破坏剖面情况
Fig.11
Stress-strain curves of uniaxial compressive strength simulated by discrete element method and corresponding rock failure image
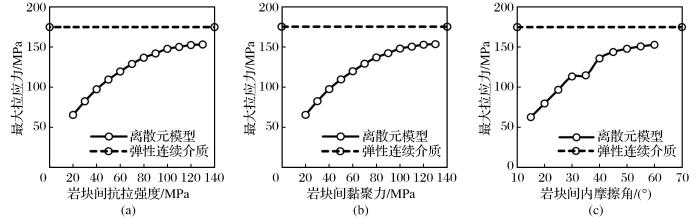
通过调用岩块间的接触刚度、黏聚力、抗拉强度和内摩擦角等相关力学参数,可以模拟不同单轴抗压强度UCS的岩石,离散元参数的调整与获取流程(Ghazvinian et al.,2014)如下:①考虑岩石晶粒平均尺寸和计算机算力,确定岩块尺寸;②根据文献资料设置岩块的弹性模量(设置较高的接触刚度实现小变形状态);③调整岩块间法向与切向接触刚度比直至达到岩石的泊松比,然后保持接触刚度比不变,调整法向接触刚度直至达到岩石的弹性模量;④调整岩块间黏聚力直至达到单轴抗拉强度,保持岩块间黏聚力不变,调整接触间黏聚力与接触抗拉强度比直至达到起裂强度(本文主要关注单轴抗压强度,起裂强度与本研究没有关联,且起裂强度较难确定,所以本文起裂强度根据文献确定);⑤如需要,根据峰后行为调整岩块间内摩擦角(内摩擦角的影响主要在峰后);⑥岩块间残余黏聚力和残余抗拉强度默认为0。
图12
图12
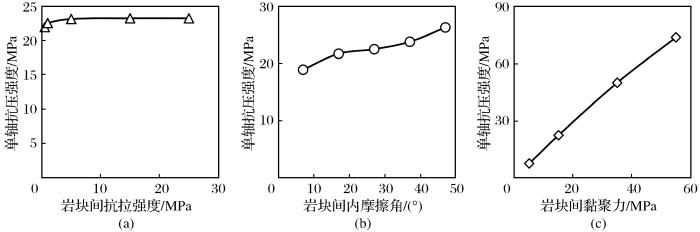
岩块间接触参数对单轴抗压强度的影响
(a)岩块间抗拉强度对单轴抗压强度的影响;(b)岩块间内摩擦角对单轴抗压强度的影响;(c)岩块间黏聚力对单轴抗压强度的影响
Fig.12
Influence of contact parameters between rock blocks on uniaxial compressive strength
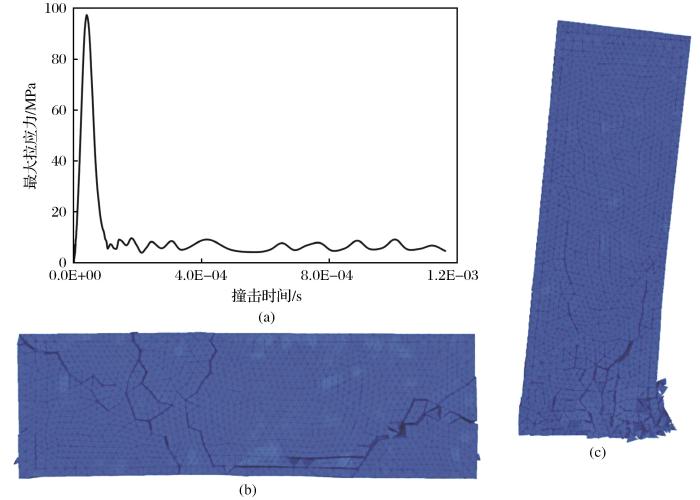
图13所示为采用离散元模型后1 kg的R1岩块在线荷载(A工况)、点荷载(D工况)撞击C储罐的结果,显然撞击过程中伴随着岩石自身的破坏。由图13可以看出,撞击开始后的较短时间内,储罐内的拉应力就达到最大值,岩石与储罐接触的一端附近发生断裂,随后应力迅速跌落并伴随着岩石的逐步开裂破损。采用连续介质线弹性模型,不考虑岩石破坏的情况下,A和D工况下产生的最大拉应力分别为175 MPa和400 MPa,考虑岩石破坏后,A和D工况下产生的最大拉应力分别为96 MPa和47 MPa,二者拉应力降幅较大。由于撞击荷载条件不同,D工况下的降低幅度远大于A工况下。显然,由于岩石自身发生破坏,岩石撞击对储罐的作用确实受到了不同程度的削弱。Jiao et al.(2005)基于爆破试验与离散元计算软件3DEC研究了三维空间冲击波在三维节理岩体内的衰减规律,结果显示冲击波在进入节理较短的距离后出现大幅衰减,远处的岩体受冲击波的作用很小,这与图13情况类似,离撞击点越近则破坏程度越高。从能量角度来说,应力波传播到岩块接触面处将发生透射和反射,导致应力波能量衰减耗散以及应力调整(王建国等,2018),削弱了撞击对储罐的影响。图14是C储罐在工况A[图10(a)]条件下,1 kg的 R2岩石(表5)的撞击灵敏性模拟计算结果。由图14可知,随着岩块间黏聚力与岩块间内摩擦角的增大,岩石撞击产生的拉应力也逐渐增大;岩块间抗拉强度对撞击产生拉应力的影响有限:当岩块间抗拉强度低于10 MPa时,撞击产生的拉应力随着岩块间抗拉强度的增加而增大,当抗拉强度超过10 MPa时撞击产生的拉应力变化较小。
图13
图13
岩石的撞击破坏
(a)工况A的撞击时程曲线;(b)工况A的岩石破坏情况;(c)工况D的岩石破坏情况
Fig.13
Impact failure of rock
图14
图14
岩块间接触参数对最大拉应力的影响
(a)岩块间抗拉强度与撞击最大拉应力的关系;(b)岩块间黏聚力与撞击最大拉应力的关系;(c)岩块间内摩擦角与撞击最大拉应力的关系;虚线为不考虑岩石破坏的结果
Fig.14
Influence of contact parameters between rock blocks on the maximum tensile stress
图15
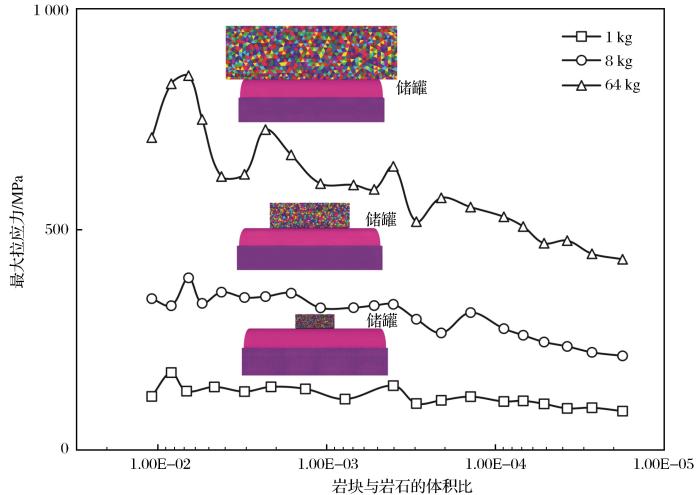
图15
岩块体积比与撞击最大拉应力的关系
Fig.15
Relationship between volume ratio of rock block and the maximum tensile stress of impact
表7 缓冲层的变形量与储罐的最大拉应力
Table 7
| 岩石质量/kg | 不同厚度和弹性模量缓冲层条件下的变形量和最大拉应力 | ||
|---|---|---|---|
| D=20 mm,E=800 MPa | D=20 mm,E=80 MPa | D=80 mm,E=100 MPa | |
| 8 | 4.85 mm/129.3 MPa | 11.67 mm/70.7 MPa | - |
| 40 | - | - | 17.15 mm/70.6 MPa |
3 结论
采用室内试验与数值计算相结合的方法,基于岩石物理特性以及深部岩石—储罐的相互作用特点,对碳化硅核废料储罐在运输安装和深埋运行中的静动力稳定性进行了初步研究,得到如下主要结论:
(1)碳化硅是脆性材料,其抗拉强度(试验测得150~200 MPa)只有单轴抗压强度的5%左右;在深埋静力条件下,埋深越大,水平与竖向地应力比越大,储罐内部的拉应力也越大。
(2)运输时自由跌落的高度越大,储罐产生的拉应力越大。此外,拉应力还与储罐与地面的接触形式或者接触面积有关,其中,点—面接触最大(跌落倾角为30°、60°),线—面接触次之(跌落倾角为0°),面—面接触最小(跌落倾角为90°);岩石撞击时储罐内的拉应力受岩石质量与撞击时岩石与储罐的接触类型控制。
(3)基于连续介质模型的分析显示,储罐有可能因运输过程中自由跌落、安装过程中受岩石撞击等动力极端荷载(点、线荷载)而发生破坏,表现在:在通常条件(线弹性模型、不考虑阻尼和缓冲层)下,储罐会因其内部动态瞬时拉应力超过抗拉强度而发生局部破坏。离散元模型考虑岩石撞击破碎,撞击附加应力大幅降低,分析认为岩块间接触面处的应力波透射和反射使得应力波能量衰减耗散,削弱了对储罐的撞击作用,离撞击点越近则岩石破碎程度越高。
(4)岩块间黏聚力和内摩擦角越大,岩石撞击力也越大,岩块间抗拉强度对撞击力的影响相对较小。随着岩块体积比减小,计算结果逐渐降低至收敛,但计算效率也在逐渐降低。为了获得可靠的结果,至少应在岩石与储罐接触点附近的区域采用较小的岩块体积比。
(5)虽然在自由跌落和岩石撞击的工况下会发生局部破坏,但通过外附一定厚度缓冲层并合理安置,储罐的静动力稳定性可以得到保证。
需要说明的是,线弹性模型计算的拉应力超过抗拉强度,虽然证明储罐损伤是发生的,但无法描述损伤的发展程度和类型。本文涉及的计算(尤其是动力学计算)仅仅是初步探究,旨在揭示核废料储罐在风险荷载场景下所受应力的量级,为今后处理与此相关的问题(如场景选择与描述、荷载与边界设置、防护措施等)提供了一种思路。
为了更准确地评价储罐安全,从数值计算角度出发,需要考虑到以下几点:阻尼的作用;采用基于材料的弹塑性模型以及损伤演化规律;采用材料的动态强度参数;更复杂、更精细的荷载场景。
http://www.goldsci.ac.cn/article/2023/1005-2518/1005-2518-2023-31-4-592.shtml
参考文献
Radiation induced corrosion of copper for spent nuclear fuel storage
[J].
Thermo-hydro-mechanical characterisation of a bentonite-based buffer material by laboratory tests and numerical back analyses
[J].
3D random Voronoi grain-based models for simulation of brittle rock damage and fabric-guided micro-fracturing
[J].
Ceramic coatings for a corrosion-resistant nuclear waste container evaluated in simulated ground water at 90 ℃
[J].
Simulation of diffusive uranium transport and sorption processes in the opalinus clay
[J].
Thermo-hydro-mechanical coupling simulation method of surrounding rock in high-level radioactive waste repository considering effective meso-thermal parameters
[J].
Numerical investigation of joint effect on shock wave propagation in jointed rock masses
[J].
Evaluation of silicon carbide (SiC) for deep borehole disposal canister
[J].
Uniaxial and triaxial compression tests of silicon carbide ceramics under quasi-static loading condition
[R].
Performance of PyC,SiC and ZrC coatings in the geologic repository
[J].
Radionuclide behaviour in the near-field of a geological repository for spent nuclear fuel
[J].
Simulation of the hydromechanical behaviour of bentonite seals for the containment of radioactive wastes
[J].
Leaching studies of nonmetallic materials for nuclear fuel immobilization containers
[C]//
The use of clay as an engineered barrier in radioactive-waste management—A review
[J].
On the mechanism of γ-radiation-induced corrosion of copper in water
[J].
High-level radioactive waste disposal in China: Update 2010
[J].
Experimental study of jointed angles impact on energy transfer characteristics of simulated rock material
[J].
THM Coupling Process in Unsaturated Bentonite Buffer Material with Construction Joints and Self-Healing Effects
[D].
Hydro-Thermal Evolution Law of Double-Layer Buffer in High-Level Radioactive Waste Repository
[D].
Numerical analysis of multi-field coupling of barrier system in deep geological repository for high-level radioactive waste
[J].
考虑细观等效热学参数的高放废物处置库围岩应力—渗流—温度耦合模拟方法
[J].
节理倾角对类岩石冲击能量传递影响的试验研究
[J].
含施工接缝的非饱和膨润土缓冲材料热—水—力耦合过程及愈合效应
[D].
高放废物处置库双层缓冲层水—热演化规律
[D].
高放废物深地质处置库屏障系统的多场耦合数值分析
[J].





 甘公网安备 62010202000672号
甘公网安备 62010202000672号