Random forests
1
2001
... 随着计算机科学的快速发展,BP人工神经网络(李强,2002)、支持向量机(SVM)(赖永标等,2006)和随机森林(RF)(Breiman,2001)等方法已被广泛应用于处理现实问题.其中,随机森林能够有效处理高维小样本数据间的复杂关系,已被广泛运用于餐饮(鞠冠章等,2022)、医疗(韩港飞等,2023)和农业(吴静,2023)等领域,但在地下工程领域的运用较少.采用计算机进行岩体质量评价,可在一定程度上提高评价效率,同时避免主观因素的影响,因此考虑将随机森林运用于岩体质量评价以弥补传统岩体质量评价方法的缺陷.同时,其他学者在研究过程中发现随机森林具备进一步优化的空间(Zhou et al.,2020),而白鲸优化(BWO)是2022年底提出的一种新的群智能优化方法,在众多群智能优化方法的性能测试中表现优异(Zhong et al.,2022).因此,本文尝试使用白鲸优化随机森林,并将优化后的随机森林用于构建岩体质量评价模型,引用工程实例数据验证模型的可行性. ...
Study of the BP Neural Network on the Stability Classification of Surrounding Rocks
2011
Engineering classification and index properties for intact rock
1
1966
... 岩体质量评价是各类地下工程设计与施工的重要环节之一.在地下工程开发时,工程岩体具有复杂多变的特性,岩体质量分级能体现岩体的物理力学性质,为工程建设的结构参数优化及施工设计提供依据(蔡美峰等,2002;文畅平,2008;赵星光等,2010;沙鹏等,2020;张钦礼等,2021).目前国内外学者对岩体质量评价进行了诸多研究,主要有单因素评价方法(Deere et al.,1966;Li et al.,2004;王明耀等,2022)和多因素评价方法(Palmstrom et al.,2006;贾明涛等,2010;邬爱清等,2014).单因素评价方法虽然简单,但过于片面,取值往往存在模糊性和随机性,忽略了地下工程的复杂性,导致评价结果与实际情况之间相差较大.多因素评价方法综合考虑多项指标,评价结果更接近实际,被广泛运用在实际工程中,但其不足之处是评价结果易受主观因素影响,且越是复杂的环境,评价耗时越多.随着研究工作的深入,涌现出距离判别法(宫凤强等,2007)、可拓学法(胡建华等,2012;凡奥奇等,2024)和TOPSIS法(胡建华等,2012)等评价方法.这些方法在一定程度上避免了评价过程中的主观性,评价精度进一步提高,但仍存在数据样本不足、计算过程冗长和评价模型普适性低等问题.综上所述,岩体质量评价方法一直在推陈出新,但尚有提升空间.随着地下工程的深度不断增加,以及智能化时代的来临,岩体质量评价方法有待进一步发展,如何更加客观、准确且高效地进行岩体质量评价是一个亟待解决的问题. ...
Evaluation of rock mass quality of phosphorite mines by topology based on optimal combination weight
2024
Application of distance discriminant analysis method to classification of engineering quality of rock masses
2007
Death risk prediction after PCI in patients with coronary heart disease and heart failure based on random forest
2023
Rock mass quality evaluation model based on improved transfer learning algorithm
2021
Rock mass quality evaluation of underground engineering based on RS-TOPSIS method
2012
Evaluation of rockmass quality based on regionalization variable optimal estimation theory and RMR system in Jinchuan mine No.3
2010
Prediction of catering data based on random forest model
2022
Application of support vector machine in classification of surrounding rock stability
2006
Stability ranking system of rockmass surrounding a large-scale underground cavern group
1
2004
... 岩体质量评价是各类地下工程设计与施工的重要环节之一.在地下工程开发时,工程岩体具有复杂多变的特性,岩体质量分级能体现岩体的物理力学性质,为工程建设的结构参数优化及施工设计提供依据(蔡美峰等,2002;文畅平,2008;赵星光等,2010;沙鹏等,2020;张钦礼等,2021).目前国内外学者对岩体质量评价进行了诸多研究,主要有单因素评价方法(Deere et al.,1966;Li et al.,2004;王明耀等,2022)和多因素评价方法(Palmstrom et al.,2006;贾明涛等,2010;邬爱清等,2014).单因素评价方法虽然简单,但过于片面,取值往往存在模糊性和随机性,忽略了地下工程的复杂性,导致评价结果与实际情况之间相差较大.多因素评价方法综合考虑多项指标,评价结果更接近实际,被广泛运用在实际工程中,但其不足之处是评价结果易受主观因素影响,且越是复杂的环境,评价耗时越多.随着研究工作的深入,涌现出距离判别法(宫凤强等,2007)、可拓学法(胡建华等,2012;凡奥奇等,2024)和TOPSIS法(胡建华等,2012)等评价方法.这些方法在一定程度上避免了评价过程中的主观性,评价精度进一步提高,但仍存在数据样本不足、计算过程冗长和评价模型普适性低等问题.综上所述,岩体质量评价方法一直在推陈出新,但尚有提升空间.随着地下工程的深度不断增加,以及智能化时代的来临,岩体质量评价方法有待进一步发展,如何更加客观、准确且高效地进行岩体质量评价是一个亟待解决的问题. ...
Study on the application of BP neural network in classification of rockmass quality
2002
A survey of swarm intelligence methods
2021
Use and misuse of rock mass classification systems with particular reference to the Q-system
2
2006
... 岩体质量评价是各类地下工程设计与施工的重要环节之一.在地下工程开发时,工程岩体具有复杂多变的特性,岩体质量分级能体现岩体的物理力学性质,为工程建设的结构参数优化及施工设计提供依据(蔡美峰等,2002;文畅平,2008;赵星光等,2010;沙鹏等,2020;张钦礼等,2021).目前国内外学者对岩体质量评价进行了诸多研究,主要有单因素评价方法(Deere et al.,1966;Li et al.,2004;王明耀等,2022)和多因素评价方法(Palmstrom et al.,2006;贾明涛等,2010;邬爱清等,2014).单因素评价方法虽然简单,但过于片面,取值往往存在模糊性和随机性,忽略了地下工程的复杂性,导致评价结果与实际情况之间相差较大.多因素评价方法综合考虑多项指标,评价结果更接近实际,被广泛运用在实际工程中,但其不足之处是评价结果易受主观因素影响,且越是复杂的环境,评价耗时越多.随着研究工作的深入,涌现出距离判别法(宫凤强等,2007)、可拓学法(胡建华等,2012;凡奥奇等,2024)和TOPSIS法(胡建华等,2012)等评价方法.这些方法在一定程度上避免了评价过程中的主观性,评价精度进一步提高,但仍存在数据样本不足、计算过程冗长和评价模型普适性低等问题.综上所述,岩体质量评价方法一直在推陈出新,但尚有提升空间.随着地下工程的深度不断增加,以及智能化时代的来临,岩体质量评价方法有待进一步发展,如何更加客观、准确且高效地进行岩体质量评价是一个亟待解决的问题. ...
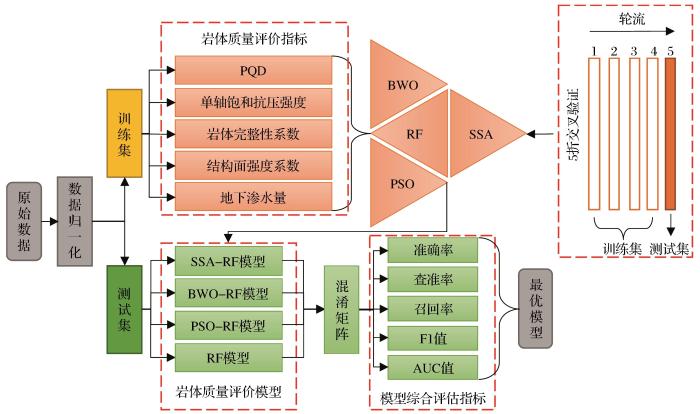
... 影响岩体质量等级的因素有很多(蔡美峰等,2002).不同学者在研究岩体质量分级时所选取的指标有所不同,各指标之间不是简单的线性关系.查阅相关文献,结合国内外工程经验,主要依据蔡广奎(2001)对于围岩分类参数的分析选取了岩体质量指标RQD(X1)、单轴饱和抗压强度(X2)、岩体完整性系数(X3)、结构面强度系数(X4)和地下渗水量(X5)5个参数作为岩体质量的评价指标.这些指标易获取,且基本反映了岩体自身岩性、地质构造影响和岩体结构等性质,众多学者采用上述指标对岩体质量评价方法进行了研究或对部分指标参数进行了相关分析(Palmstrom et al.,2006;宫凤强等,2007;贾明涛等,2010;胡建华等,2012;邬爱清等,2014).依据相关文献(李强,2002;赖永标等,2006;宫凤强等,2007;胡建华等,2012;邬爱清等,2014),基于《工程岩体分级标准》(中华人民共和国水利部,2014),将岩体质量划分为5个等级:Ⅰ(稳定)、Ⅱ(较稳定)、Ⅲ(基本稳定)、Ⅳ(不稳定)和Ⅴ(极不稳定),分级标准详见表1. ...
Evaluation of tunnel rock quality with routh sets theory and artificial neural networks
2008
Improvement of BQ classification for layered rock mass quality index in tunnel engineering
2020
Evaluation of underground cavern rock quality based on uncertainty measure theory
2011
Adaptability of TBM and classification method of large deformation of soft rock
2022
Classification of rock-mass stability based on attributive mathematical theory
2008
Engineering rock mass classification method based on rock mass quality index BQ for rock slope
2014
Design of apple classification system based on improved random forest
2023
Concept of green mining and its technical framework
2007
Rock mass quality classification based on Mamdani FIS model and RMR method
2021
A comparative study of SSA-BPNN,SSA-ENN,and SSA-SVR models for predicting the thickness of an excavation damaged zone around the roadway in rock
2
2022
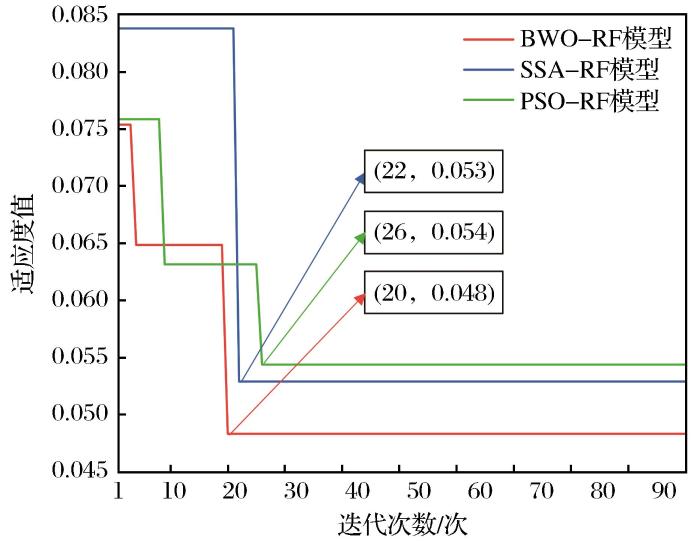
... 根据上述BWO-RF模型构建原理进行模型构建.本文在模型构建过程中,加入了5折交叉验证,可有效提高RF模型的泛化性能,尤其是训练好的模型对新引入数据集的预测表现上,在一定程度上减少了模型的过拟合.麻雀搜索算法(SSA)是2020年提出的拥有较高搜索效率且操作简单的群智能优化方法(Zhao et al.,2022),粒子群优化(PSO)是一种经典的群智能优化方法,具有较强的搜索能力且收敛速度快(刘雪等,2021).为了提高模型验证分析效果,在构建BWO-RF模型的同时,运用SSA和PSO优化RF,得到SSA-RF模型和PSO-RF模型,各优化方法输出的最优ntree、mtry参数组合及RF模型默认ntree、mtry参数组合见表3. ...
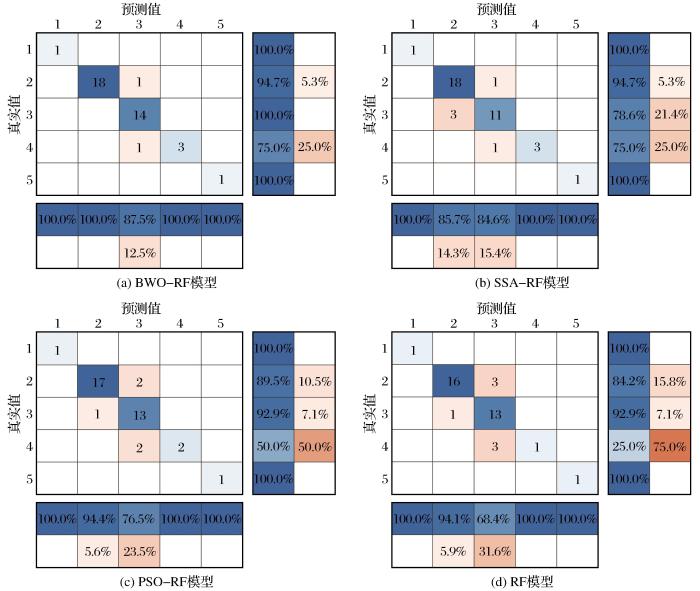
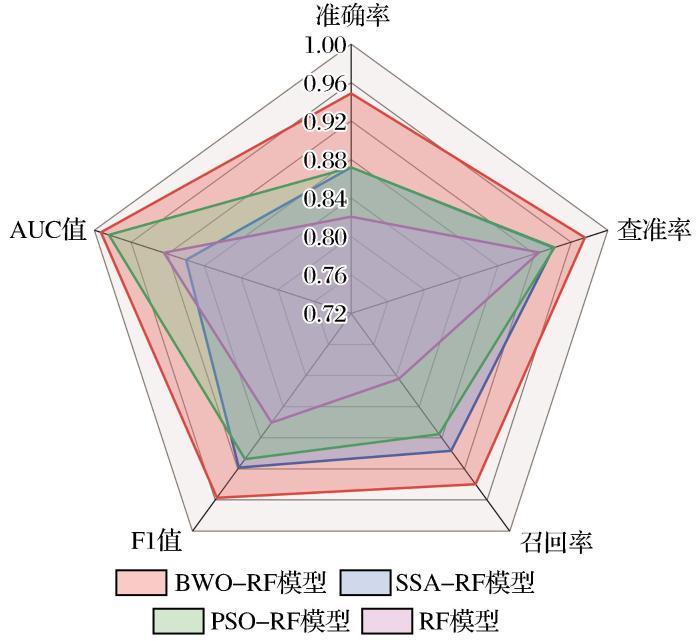
... 评价模型的优劣深受样本数据和评价方法的影响.学者们对计算机科学与边坡稳定性和岩体质量等领域相关评价模型的结合进行了诸多研究.如:针对边坡稳定性评价模型(Zhao et al.,2022)的研究积累了庞大的样本数据.相比之下,岩体质量评价模型的样本数据还有补充的空间.与此同时,边坡稳定性评价模型常采用二分类的评价方法,而岩体质量评价模型常采用多分类的评价方法,其所需评价的结果种类更多.综合上述2个方面原因,本文所构建的4种评价模型并未呈现出评价准确率均高于90%且相差较小的情况.针对该情况,本文补充了BWO-RF模型的工程应用实例,从而进一步验证模型的性能. ...
Influence of dilation on rock mass displacement around underground excavations—A case study of Donkin-Morien Tunnel in Canada
2010
Beluga whale optimization:A novel nature-inspired metaheuristic algorithm
3
2022
... 随着计算机科学的快速发展,BP人工神经网络(李强,2002)、支持向量机(SVM)(赖永标等,2006)和随机森林(RF)(Breiman,2001)等方法已被广泛应用于处理现实问题.其中,随机森林能够有效处理高维小样本数据间的复杂关系,已被广泛运用于餐饮(鞠冠章等,2022)、医疗(韩港飞等,2023)和农业(吴静,2023)等领域,但在地下工程领域的运用较少.采用计算机进行岩体质量评价,可在一定程度上提高评价效率,同时避免主观因素的影响,因此考虑将随机森林运用于岩体质量评价以弥补传统岩体质量评价方法的缺陷.同时,其他学者在研究过程中发现随机森林具备进一步优化的空间(Zhou et al.,2020),而白鲸优化(BWO)是2022年底提出的一种新的群智能优化方法,在众多群智能优化方法的性能测试中表现优异(Zhong et al.,2022).因此,本文尝试使用白鲸优化随机森林,并将优化后的随机森林用于构建岩体质量评价模型,引用工程实例数据验证模型的可行性. ...
... 白鲸优化(Beluga Whale Optimization,BWO)(Zhong et al.,2022)是于2022年提出的一种群智能优化方法,在解决一维和多维问题上均有很好的表现,且展现了极强的基准函数可扩展性分析能力,是求解最优化问题的良好选择. ...
... BWO具有良好的全局收敛性,在与众多群智能优化方法的对比试验中,具有不错的表现,一维问题和多维问题均可得到很好的解决,同时在具体的工程实例验证中也展现出较强竞争力(Zhong et al.,2022).RF能有效解决多参数之间的非线性问题,具有预测精度高和训练速度快等优势,而影响RF模型的关键参数主要有决策树的数量(ntree)和分裂节点(mtry),将这些参数作为BWO的寻优目标,取最终模型预测误差最小的参数组合作为最优参数组合,以此构建岩体质量评价模型.BWO-RF岩体质量评价模型构建流程见图1. ...
Prediction of ground vibration induced by blasting operations through the use of the Bayesian Network and random forest models
2
2020
... 随着计算机科学的快速发展,BP人工神经网络(李强,2002)、支持向量机(SVM)(赖永标等,2006)和随机森林(RF)(Breiman,2001)等方法已被广泛应用于处理现实问题.其中,随机森林能够有效处理高维小样本数据间的复杂关系,已被广泛运用于餐饮(鞠冠章等,2022)、医疗(韩港飞等,2023)和农业(吴静,2023)等领域,但在地下工程领域的运用较少.采用计算机进行岩体质量评价,可在一定程度上提高评价效率,同时避免主观因素的影响,因此考虑将随机森林运用于岩体质量评价以弥补传统岩体质量评价方法的缺陷.同时,其他学者在研究过程中发现随机森林具备进一步优化的空间(Zhou et al.,2020),而白鲸优化(BWO)是2022年底提出的一种新的群智能优化方法,在众多群智能优化方法的性能测试中表现优异(Zhong et al.,2022).因此,本文尝试使用白鲸优化随机森林,并将优化后的随机森林用于构建岩体质量评价模型,引用工程实例数据验证模型的可行性. ...
... 随机森林(Random Forest,RF)是一种由决策树和bagging框架构成的集成方法(Zhou et al.,2020).该方法采用Bootstrap抽样,从训练集中随机抽取一定样本形成一个Bootstrap训练集,为每个Bootstrap训练集建立决策树,基于Bootstrap训练集,构建袋外数据,其中包含Bootstrap训练集中不存在的样本,在袋外数据误差估计过程中,袋外数据扮演测试集的角色,因此不需要创建另一个测试集. ...
围岩稳定性分类的BP网络模型的研究
1
2001
... 影响岩体质量等级的因素有很多(蔡美峰等,2002).不同学者在研究岩体质量分级时所选取的指标有所不同,各指标之间不是简单的线性关系.查阅相关文献,结合国内外工程经验,主要依据蔡广奎(2001)对于围岩分类参数的分析选取了岩体质量指标RQD(X1)、单轴饱和抗压强度(X2)、岩体完整性系数(X3)、结构面强度系数(X4)和地下渗水量(X5)5个参数作为岩体质量的评价指标.这些指标易获取,且基本反映了岩体自身岩性、地质构造影响和岩体结构等性质,众多学者采用上述指标对岩体质量评价方法进行了研究或对部分指标参数进行了相关分析(Palmstrom et al.,2006;宫凤强等,2007;贾明涛等,2010;胡建华等,2012;邬爱清等,2014).依据相关文献(李强,2002;赖永标等,2006;宫凤强等,2007;胡建华等,2012;邬爱清等,2014),基于《工程岩体分级标准》(中华人民共和国水利部,2014),将岩体质量划分为5个等级:Ⅰ(稳定)、Ⅱ(较稳定)、Ⅲ(基本稳定)、Ⅳ(不稳定)和Ⅴ(极不稳定),分级标准详见表1. ...
2
2002
... 岩体质量评价是各类地下工程设计与施工的重要环节之一.在地下工程开发时,工程岩体具有复杂多变的特性,岩体质量分级能体现岩体的物理力学性质,为工程建设的结构参数优化及施工设计提供依据(蔡美峰等,2002;文畅平,2008;赵星光等,2010;沙鹏等,2020;张钦礼等,2021).目前国内外学者对岩体质量评价进行了诸多研究,主要有单因素评价方法(Deere et al.,1966;Li et al.,2004;王明耀等,2022)和多因素评价方法(Palmstrom et al.,2006;贾明涛等,2010;邬爱清等,2014).单因素评价方法虽然简单,但过于片面,取值往往存在模糊性和随机性,忽略了地下工程的复杂性,导致评价结果与实际情况之间相差较大.多因素评价方法综合考虑多项指标,评价结果更接近实际,被广泛运用在实际工程中,但其不足之处是评价结果易受主观因素影响,且越是复杂的环境,评价耗时越多.随着研究工作的深入,涌现出距离判别法(宫凤强等,2007)、可拓学法(胡建华等,2012;凡奥奇等,2024)和TOPSIS法(胡建华等,2012)等评价方法.这些方法在一定程度上避免了评价过程中的主观性,评价精度进一步提高,但仍存在数据样本不足、计算过程冗长和评价模型普适性低等问题.综上所述,岩体质量评价方法一直在推陈出新,但尚有提升空间.随着地下工程的深度不断增加,以及智能化时代的来临,岩体质量评价方法有待进一步发展,如何更加客观、准确且高效地进行岩体质量评价是一个亟待解决的问题. ...
... 影响岩体质量等级的因素有很多(蔡美峰等,2002).不同学者在研究岩体质量分级时所选取的指标有所不同,各指标之间不是简单的线性关系.查阅相关文献,结合国内外工程经验,主要依据蔡广奎(2001)对于围岩分类参数的分析选取了岩体质量指标RQD(X1)、单轴饱和抗压强度(X2)、岩体完整性系数(X3)、结构面强度系数(X4)和地下渗水量(X5)5个参数作为岩体质量的评价指标.这些指标易获取,且基本反映了岩体自身岩性、地质构造影响和岩体结构等性质,众多学者采用上述指标对岩体质量评价方法进行了研究或对部分指标参数进行了相关分析(Palmstrom et al.,2006;宫凤强等,2007;贾明涛等,2010;胡建华等,2012;邬爱清等,2014).依据相关文献(李强,2002;赖永标等,2006;宫凤强等,2007;胡建华等,2012;邬爱清等,2014),基于《工程岩体分级标准》(中华人民共和国水利部,2014),将岩体质量划分为5个等级:Ⅰ(稳定)、Ⅱ(较稳定)、Ⅲ(基本稳定)、Ⅳ(不稳定)和Ⅴ(极不稳定),分级标准详见表1. ...
基于优化组合赋权的可拓学磷矿山岩体质量评价
1
2024
... 岩体质量评价是各类地下工程设计与施工的重要环节之一.在地下工程开发时,工程岩体具有复杂多变的特性,岩体质量分级能体现岩体的物理力学性质,为工程建设的结构参数优化及施工设计提供依据(蔡美峰等,2002;文畅平,2008;赵星光等,2010;沙鹏等,2020;张钦礼等,2021).目前国内外学者对岩体质量评价进行了诸多研究,主要有单因素评价方法(Deere et al.,1966;Li et al.,2004;王明耀等,2022)和多因素评价方法(Palmstrom et al.,2006;贾明涛等,2010;邬爱清等,2014).单因素评价方法虽然简单,但过于片面,取值往往存在模糊性和随机性,忽略了地下工程的复杂性,导致评价结果与实际情况之间相差较大.多因素评价方法综合考虑多项指标,评价结果更接近实际,被广泛运用在实际工程中,但其不足之处是评价结果易受主观因素影响,且越是复杂的环境,评价耗时越多.随着研究工作的深入,涌现出距离判别法(宫凤强等,2007)、可拓学法(胡建华等,2012;凡奥奇等,2024)和TOPSIS法(胡建华等,2012)等评价方法.这些方法在一定程度上避免了评价过程中的主观性,评价精度进一步提高,但仍存在数据样本不足、计算过程冗长和评价模型普适性低等问题.综上所述,岩体质量评价方法一直在推陈出新,但尚有提升空间.随着地下工程的深度不断增加,以及智能化时代的来临,岩体质量评价方法有待进一步发展,如何更加客观、准确且高效地进行岩体质量评价是一个亟待解决的问题. ...
距离判别分析法在岩体质量等级分类中的应用
3
2007
... 岩体质量评价是各类地下工程设计与施工的重要环节之一.在地下工程开发时,工程岩体具有复杂多变的特性,岩体质量分级能体现岩体的物理力学性质,为工程建设的结构参数优化及施工设计提供依据(蔡美峰等,2002;文畅平,2008;赵星光等,2010;沙鹏等,2020;张钦礼等,2021).目前国内外学者对岩体质量评价进行了诸多研究,主要有单因素评价方法(Deere et al.,1966;Li et al.,2004;王明耀等,2022)和多因素评价方法(Palmstrom et al.,2006;贾明涛等,2010;邬爱清等,2014).单因素评价方法虽然简单,但过于片面,取值往往存在模糊性和随机性,忽略了地下工程的复杂性,导致评价结果与实际情况之间相差较大.多因素评价方法综合考虑多项指标,评价结果更接近实际,被广泛运用在实际工程中,但其不足之处是评价结果易受主观因素影响,且越是复杂的环境,评价耗时越多.随着研究工作的深入,涌现出距离判别法(宫凤强等,2007)、可拓学法(胡建华等,2012;凡奥奇等,2024)和TOPSIS法(胡建华等,2012)等评价方法.这些方法在一定程度上避免了评价过程中的主观性,评价精度进一步提高,但仍存在数据样本不足、计算过程冗长和评价模型普适性低等问题.综上所述,岩体质量评价方法一直在推陈出新,但尚有提升空间.随着地下工程的深度不断增加,以及智能化时代的来临,岩体质量评价方法有待进一步发展,如何更加客观、准确且高效地进行岩体质量评价是一个亟待解决的问题. ...
... 影响岩体质量等级的因素有很多(蔡美峰等,2002).不同学者在研究岩体质量分级时所选取的指标有所不同,各指标之间不是简单的线性关系.查阅相关文献,结合国内外工程经验,主要依据蔡广奎(2001)对于围岩分类参数的分析选取了岩体质量指标RQD(X1)、单轴饱和抗压强度(X2)、岩体完整性系数(X3)、结构面强度系数(X4)和地下渗水量(X5)5个参数作为岩体质量的评价指标.这些指标易获取,且基本反映了岩体自身岩性、地质构造影响和岩体结构等性质,众多学者采用上述指标对岩体质量评价方法进行了研究或对部分指标参数进行了相关分析(Palmstrom et al.,2006;宫凤强等,2007;贾明涛等,2010;胡建华等,2012;邬爱清等,2014).依据相关文献(李强,2002;赖永标等,2006;宫凤强等,2007;胡建华等,2012;邬爱清等,2014),基于《工程岩体分级标准》(中华人民共和国水利部,2014),将岩体质量划分为5个等级:Ⅰ(稳定)、Ⅱ(较稳定)、Ⅲ(基本稳定)、Ⅳ(不稳定)和Ⅴ(极不稳定),分级标准详见表1. ...
... ;宫凤强等,2007;胡建华等,2012;邬爱清等,2014),基于《工程岩体分级标准》(中华人民共和国水利部,2014),将岩体质量划分为5个等级:Ⅰ(稳定)、Ⅱ(较稳定)、Ⅲ(基本稳定)、Ⅳ(不稳定)和Ⅴ(极不稳定),分级标准详见表1. ...
基于随机森林的冠心病合并心力衰竭患者PCI术后死亡风险预测研究
1
2023
... 随着计算机科学的快速发展,BP人工神经网络(李强,2002)、支持向量机(SVM)(赖永标等,2006)和随机森林(RF)(Breiman,2001)等方法已被广泛应用于处理现实问题.其中,随机森林能够有效处理高维小样本数据间的复杂关系,已被广泛运用于餐饮(鞠冠章等,2022)、医疗(韩港飞等,2023)和农业(吴静,2023)等领域,但在地下工程领域的运用较少.采用计算机进行岩体质量评价,可在一定程度上提高评价效率,同时避免主观因素的影响,因此考虑将随机森林运用于岩体质量评价以弥补传统岩体质量评价方法的缺陷.同时,其他学者在研究过程中发现随机森林具备进一步优化的空间(Zhou et al.,2020),而白鲸优化(BWO)是2022年底提出的一种新的群智能优化方法,在众多群智能优化方法的性能测试中表现优异(Zhong et al.,2022).因此,本文尝试使用白鲸优化随机森林,并将优化后的随机森林用于构建岩体质量评价模型,引用工程实例数据验证模型的可行性. ...
基于改进迁移学习算法的岩体质量评价模型
1
2021
... 从已有文献(许家林等,2007;邱道宏等,2008;唐海等,2011;胡建华等,2021)和实际工程中搜集多个地区实测的131组地下工程岩体数据,建立了本文研究所需的数据库.其中,从文献中搜集的数据均为文献作者从相应项目中获取的真实数据,本文作者基于所承担的项目通过现场试验获取数据,对整个数据库进行了补充,数据库中每组评价参数对应的评价结果均来自对应的项目报告,在本文中被视为真实值.将数据库按7∶3的比例划分为训练集和测试集,用于岩体质量评价模型的训练构建及验证分析.模型构建过程完全依托于训练集,未接触过测试集数据,因此通过测试集对模型进行测试时,模型仅根据构建过程中训练出来的内生逻辑对测试集的输入参数进行预测,将模型预测值与测试集中的真实值进行对比即可评判其准确性,地下工程岩体数据库(部分)见表2. ...
基于RS-TOPSIS法的地下工程岩体质量评价
4
2012
... 岩体质量评价是各类地下工程设计与施工的重要环节之一.在地下工程开发时,工程岩体具有复杂多变的特性,岩体质量分级能体现岩体的物理力学性质,为工程建设的结构参数优化及施工设计提供依据(蔡美峰等,2002;文畅平,2008;赵星光等,2010;沙鹏等,2020;张钦礼等,2021).目前国内外学者对岩体质量评价进行了诸多研究,主要有单因素评价方法(Deere et al.,1966;Li et al.,2004;王明耀等,2022)和多因素评价方法(Palmstrom et al.,2006;贾明涛等,2010;邬爱清等,2014).单因素评价方法虽然简单,但过于片面,取值往往存在模糊性和随机性,忽略了地下工程的复杂性,导致评价结果与实际情况之间相差较大.多因素评价方法综合考虑多项指标,评价结果更接近实际,被广泛运用在实际工程中,但其不足之处是评价结果易受主观因素影响,且越是复杂的环境,评价耗时越多.随着研究工作的深入,涌现出距离判别法(宫凤强等,2007)、可拓学法(胡建华等,2012;凡奥奇等,2024)和TOPSIS法(胡建华等,2012)等评价方法.这些方法在一定程度上避免了评价过程中的主观性,评价精度进一步提高,但仍存在数据样本不足、计算过程冗长和评价模型普适性低等问题.综上所述,岩体质量评价方法一直在推陈出新,但尚有提升空间.随着地下工程的深度不断增加,以及智能化时代的来临,岩体质量评价方法有待进一步发展,如何更加客观、准确且高效地进行岩体质量评价是一个亟待解决的问题. ...
... )和TOPSIS法(胡建华等,2012)等评价方法.这些方法在一定程度上避免了评价过程中的主观性,评价精度进一步提高,但仍存在数据样本不足、计算过程冗长和评价模型普适性低等问题.综上所述,岩体质量评价方法一直在推陈出新,但尚有提升空间.随着地下工程的深度不断增加,以及智能化时代的来临,岩体质量评价方法有待进一步发展,如何更加客观、准确且高效地进行岩体质量评价是一个亟待解决的问题. ...
... 影响岩体质量等级的因素有很多(蔡美峰等,2002).不同学者在研究岩体质量分级时所选取的指标有所不同,各指标之间不是简单的线性关系.查阅相关文献,结合国内外工程经验,主要依据蔡广奎(2001)对于围岩分类参数的分析选取了岩体质量指标RQD(X1)、单轴饱和抗压强度(X2)、岩体完整性系数(X3)、结构面强度系数(X4)和地下渗水量(X5)5个参数作为岩体质量的评价指标.这些指标易获取,且基本反映了岩体自身岩性、地质构造影响和岩体结构等性质,众多学者采用上述指标对岩体质量评价方法进行了研究或对部分指标参数进行了相关分析(Palmstrom et al.,2006;宫凤强等,2007;贾明涛等,2010;胡建华等,2012;邬爱清等,2014).依据相关文献(李强,2002;赖永标等,2006;宫凤强等,2007;胡建华等,2012;邬爱清等,2014),基于《工程岩体分级标准》(中华人民共和国水利部,2014),将岩体质量划分为5个等级:Ⅰ(稳定)、Ⅱ(较稳定)、Ⅲ(基本稳定)、Ⅳ(不稳定)和Ⅴ(极不稳定),分级标准详见表1. ...
... ;胡建华等,2012;邬爱清等,2014),基于《工程岩体分级标准》(中华人民共和国水利部,2014),将岩体质量划分为5个等级:Ⅰ(稳定)、Ⅱ(较稳定)、Ⅲ(基本稳定)、Ⅳ(不稳定)和Ⅴ(极不稳定),分级标准详见表1. ...
基于区域化变量及RMR评价体系的金川Ⅲ矿区矿岩质量评价
2
2010
... 岩体质量评价是各类地下工程设计与施工的重要环节之一.在地下工程开发时,工程岩体具有复杂多变的特性,岩体质量分级能体现岩体的物理力学性质,为工程建设的结构参数优化及施工设计提供依据(蔡美峰等,2002;文畅平,2008;赵星光等,2010;沙鹏等,2020;张钦礼等,2021).目前国内外学者对岩体质量评价进行了诸多研究,主要有单因素评价方法(Deere et al.,1966;Li et al.,2004;王明耀等,2022)和多因素评价方法(Palmstrom et al.,2006;贾明涛等,2010;邬爱清等,2014).单因素评价方法虽然简单,但过于片面,取值往往存在模糊性和随机性,忽略了地下工程的复杂性,导致评价结果与实际情况之间相差较大.多因素评价方法综合考虑多项指标,评价结果更接近实际,被广泛运用在实际工程中,但其不足之处是评价结果易受主观因素影响,且越是复杂的环境,评价耗时越多.随着研究工作的深入,涌现出距离判别法(宫凤强等,2007)、可拓学法(胡建华等,2012;凡奥奇等,2024)和TOPSIS法(胡建华等,2012)等评价方法.这些方法在一定程度上避免了评价过程中的主观性,评价精度进一步提高,但仍存在数据样本不足、计算过程冗长和评价模型普适性低等问题.综上所述,岩体质量评价方法一直在推陈出新,但尚有提升空间.随着地下工程的深度不断增加,以及智能化时代的来临,岩体质量评价方法有待进一步发展,如何更加客观、准确且高效地进行岩体质量评价是一个亟待解决的问题. ...
... 影响岩体质量等级的因素有很多(蔡美峰等,2002).不同学者在研究岩体质量分级时所选取的指标有所不同,各指标之间不是简单的线性关系.查阅相关文献,结合国内外工程经验,主要依据蔡广奎(2001)对于围岩分类参数的分析选取了岩体质量指标RQD(X1)、单轴饱和抗压强度(X2)、岩体完整性系数(X3)、结构面强度系数(X4)和地下渗水量(X5)5个参数作为岩体质量的评价指标.这些指标易获取,且基本反映了岩体自身岩性、地质构造影响和岩体结构等性质,众多学者采用上述指标对岩体质量评价方法进行了研究或对部分指标参数进行了相关分析(Palmstrom et al.,2006;宫凤强等,2007;贾明涛等,2010;胡建华等,2012;邬爱清等,2014).依据相关文献(李强,2002;赖永标等,2006;宫凤强等,2007;胡建华等,2012;邬爱清等,2014),基于《工程岩体分级标准》(中华人民共和国水利部,2014),将岩体质量划分为5个等级:Ⅰ(稳定)、Ⅱ(较稳定)、Ⅲ(基本稳定)、Ⅳ(不稳定)和Ⅴ(极不稳定),分级标准详见表1. ...
基于随机森林模型的餐饮数据预测
1
2022
... 随着计算机科学的快速发展,BP人工神经网络(李强,2002)、支持向量机(SVM)(赖永标等,2006)和随机森林(RF)(Breiman,2001)等方法已被广泛应用于处理现实问题.其中,随机森林能够有效处理高维小样本数据间的复杂关系,已被广泛运用于餐饮(鞠冠章等,2022)、医疗(韩港飞等,2023)和农业(吴静,2023)等领域,但在地下工程领域的运用较少.采用计算机进行岩体质量评价,可在一定程度上提高评价效率,同时避免主观因素的影响,因此考虑将随机森林运用于岩体质量评价以弥补传统岩体质量评价方法的缺陷.同时,其他学者在研究过程中发现随机森林具备进一步优化的空间(Zhou et al.,2020),而白鲸优化(BWO)是2022年底提出的一种新的群智能优化方法,在众多群智能优化方法的性能测试中表现优异(Zhong et al.,2022).因此,本文尝试使用白鲸优化随机森林,并将优化后的随机森林用于构建岩体质量评价模型,引用工程实例数据验证模型的可行性. ...
支持向量机在围岩稳定性分类中的应用
2
2006
... 随着计算机科学的快速发展,BP人工神经网络(李强,2002)、支持向量机(SVM)(赖永标等,2006)和随机森林(RF)(Breiman,2001)等方法已被广泛应用于处理现实问题.其中,随机森林能够有效处理高维小样本数据间的复杂关系,已被广泛运用于餐饮(鞠冠章等,2022)、医疗(韩港飞等,2023)和农业(吴静,2023)等领域,但在地下工程领域的运用较少.采用计算机进行岩体质量评价,可在一定程度上提高评价效率,同时避免主观因素的影响,因此考虑将随机森林运用于岩体质量评价以弥补传统岩体质量评价方法的缺陷.同时,其他学者在研究过程中发现随机森林具备进一步优化的空间(Zhou et al.,2020),而白鲸优化(BWO)是2022年底提出的一种新的群智能优化方法,在众多群智能优化方法的性能测试中表现优异(Zhong et al.,2022).因此,本文尝试使用白鲸优化随机森林,并将优化后的随机森林用于构建岩体质量评价模型,引用工程实例数据验证模型的可行性. ...
... 影响岩体质量等级的因素有很多(蔡美峰等,2002).不同学者在研究岩体质量分级时所选取的指标有所不同,各指标之间不是简单的线性关系.查阅相关文献,结合国内外工程经验,主要依据蔡广奎(2001)对于围岩分类参数的分析选取了岩体质量指标RQD(X1)、单轴饱和抗压强度(X2)、岩体完整性系数(X3)、结构面强度系数(X4)和地下渗水量(X5)5个参数作为岩体质量的评价指标.这些指标易获取,且基本反映了岩体自身岩性、地质构造影响和岩体结构等性质,众多学者采用上述指标对岩体质量评价方法进行了研究或对部分指标参数进行了相关分析(Palmstrom et al.,2006;宫凤强等,2007;贾明涛等,2010;胡建华等,2012;邬爱清等,2014).依据相关文献(李强,2002;赖永标等,2006;宫凤强等,2007;胡建华等,2012;邬爱清等,2014),基于《工程岩体分级标准》(中华人民共和国水利部,2014),将岩体质量划分为5个等级:Ⅰ(稳定)、Ⅱ(较稳定)、Ⅲ(基本稳定)、Ⅳ(不稳定)和Ⅴ(极不稳定),分级标准详见表1. ...
BP神经网络在工程岩体质量分级中的应用研究
2
2002
... 随着计算机科学的快速发展,BP人工神经网络(李强,2002)、支持向量机(SVM)(赖永标等,2006)和随机森林(RF)(Breiman,2001)等方法已被广泛应用于处理现实问题.其中,随机森林能够有效处理高维小样本数据间的复杂关系,已被广泛运用于餐饮(鞠冠章等,2022)、医疗(韩港飞等,2023)和农业(吴静,2023)等领域,但在地下工程领域的运用较少.采用计算机进行岩体质量评价,可在一定程度上提高评价效率,同时避免主观因素的影响,因此考虑将随机森林运用于岩体质量评价以弥补传统岩体质量评价方法的缺陷.同时,其他学者在研究过程中发现随机森林具备进一步优化的空间(Zhou et al.,2020),而白鲸优化(BWO)是2022年底提出的一种新的群智能优化方法,在众多群智能优化方法的性能测试中表现优异(Zhong et al.,2022).因此,本文尝试使用白鲸优化随机森林,并将优化后的随机森林用于构建岩体质量评价模型,引用工程实例数据验证模型的可行性. ...
... 影响岩体质量等级的因素有很多(蔡美峰等,2002).不同学者在研究岩体质量分级时所选取的指标有所不同,各指标之间不是简单的线性关系.查阅相关文献,结合国内外工程经验,主要依据蔡广奎(2001)对于围岩分类参数的分析选取了岩体质量指标RQD(X1)、单轴饱和抗压强度(X2)、岩体完整性系数(X3)、结构面强度系数(X4)和地下渗水量(X5)5个参数作为岩体质量的评价指标.这些指标易获取,且基本反映了岩体自身岩性、地质构造影响和岩体结构等性质,众多学者采用上述指标对岩体质量评价方法进行了研究或对部分指标参数进行了相关分析(Palmstrom et al.,2006;宫凤强等,2007;贾明涛等,2010;胡建华等,2012;邬爱清等,2014).依据相关文献(李强,2002;赖永标等,2006;宫凤强等,2007;胡建华等,2012;邬爱清等,2014),基于《工程岩体分级标准》(中华人民共和国水利部,2014),将岩体质量划分为5个等级:Ⅰ(稳定)、Ⅱ(较稳定)、Ⅲ(基本稳定)、Ⅳ(不稳定)和Ⅴ(极不稳定),分级标准详见表1. ...
群智能算法研究综述
1
2021
... 根据上述BWO-RF模型构建原理进行模型构建.本文在模型构建过程中,加入了5折交叉验证,可有效提高RF模型的泛化性能,尤其是训练好的模型对新引入数据集的预测表现上,在一定程度上减少了模型的过拟合.麻雀搜索算法(SSA)是2020年提出的拥有较高搜索效率且操作简单的群智能优化方法(Zhao et al.,2022),粒子群优化(PSO)是一种经典的群智能优化方法,具有较强的搜索能力且收敛速度快(刘雪等,2021).为了提高模型验证分析效果,在构建BWO-RF模型的同时,运用SSA和PSO优化RF,得到SSA-RF模型和PSO-RF模型,各优化方法输出的最优ntree、mtry参数组合及RF模型默认ntree、mtry参数组合见表3. ...
基于粗糙集和人工神经网络的洞室岩体质量评价
1
2008
... 从已有文献(许家林等,2007;邱道宏等,2008;唐海等,2011;胡建华等,2021)和实际工程中搜集多个地区实测的131组地下工程岩体数据,建立了本文研究所需的数据库.其中,从文献中搜集的数据均为文献作者从相应项目中获取的真实数据,本文作者基于所承担的项目通过现场试验获取数据,对整个数据库进行了补充,数据库中每组评价参数对应的评价结果均来自对应的项目报告,在本文中被视为真实值.将数据库按7∶3的比例划分为训练集和测试集,用于岩体质量评价模型的训练构建及验证分析.模型构建过程完全依托于训练集,未接触过测试集数据,因此通过测试集对模型进行测试时,模型仅根据构建过程中训练出来的内生逻辑对测试集的输入参数进行预测,将模型预测值与测试集中的真实值进行对比即可评判其准确性,地下工程岩体数据库(部分)见表2. ...
隧道层状岩体质量评价的BQ分级改进
1
2020
... 岩体质量评价是各类地下工程设计与施工的重要环节之一.在地下工程开发时,工程岩体具有复杂多变的特性,岩体质量分级能体现岩体的物理力学性质,为工程建设的结构参数优化及施工设计提供依据(蔡美峰等,2002;文畅平,2008;赵星光等,2010;沙鹏等,2020;张钦礼等,2021).目前国内外学者对岩体质量评价进行了诸多研究,主要有单因素评价方法(Deere et al.,1966;Li et al.,2004;王明耀等,2022)和多因素评价方法(Palmstrom et al.,2006;贾明涛等,2010;邬爱清等,2014).单因素评价方法虽然简单,但过于片面,取值往往存在模糊性和随机性,忽略了地下工程的复杂性,导致评价结果与实际情况之间相差较大.多因素评价方法综合考虑多项指标,评价结果更接近实际,被广泛运用在实际工程中,但其不足之处是评价结果易受主观因素影响,且越是复杂的环境,评价耗时越多.随着研究工作的深入,涌现出距离判别法(宫凤强等,2007)、可拓学法(胡建华等,2012;凡奥奇等,2024)和TOPSIS法(胡建华等,2012)等评价方法.这些方法在一定程度上避免了评价过程中的主观性,评价精度进一步提高,但仍存在数据样本不足、计算过程冗长和评价模型普适性低等问题.综上所述,岩体质量评价方法一直在推陈出新,但尚有提升空间.随着地下工程的深度不断增加,以及智能化时代的来临,岩体质量评价方法有待进一步发展,如何更加客观、准确且高效地进行岩体质量评价是一个亟待解决的问题. ...
基于未确知测度理论的地下洞室岩体质量评价
1
2011
... 从已有文献(许家林等,2007;邱道宏等,2008;唐海等,2011;胡建华等,2021)和实际工程中搜集多个地区实测的131组地下工程岩体数据,建立了本文研究所需的数据库.其中,从文献中搜集的数据均为文献作者从相应项目中获取的真实数据,本文作者基于所承担的项目通过现场试验获取数据,对整个数据库进行了补充,数据库中每组评价参数对应的评价结果均来自对应的项目报告,在本文中被视为真实值.将数据库按7∶3的比例划分为训练集和测试集,用于岩体质量评价模型的训练构建及验证分析.模型构建过程完全依托于训练集,未接触过测试集数据,因此通过测试集对模型进行测试时,模型仅根据构建过程中训练出来的内生逻辑对测试集的输入参数进行预测,将模型预测值与测试集中的真实值进行对比即可评判其准确性,地下工程岩体数据库(部分)见表2. ...
软岩大变形分类分级方法及TBM适应性
1
2022
... 岩体质量评价是各类地下工程设计与施工的重要环节之一.在地下工程开发时,工程岩体具有复杂多变的特性,岩体质量分级能体现岩体的物理力学性质,为工程建设的结构参数优化及施工设计提供依据(蔡美峰等,2002;文畅平,2008;赵星光等,2010;沙鹏等,2020;张钦礼等,2021).目前国内外学者对岩体质量评价进行了诸多研究,主要有单因素评价方法(Deere et al.,1966;Li et al.,2004;王明耀等,2022)和多因素评价方法(Palmstrom et al.,2006;贾明涛等,2010;邬爱清等,2014).单因素评价方法虽然简单,但过于片面,取值往往存在模糊性和随机性,忽略了地下工程的复杂性,导致评价结果与实际情况之间相差较大.多因素评价方法综合考虑多项指标,评价结果更接近实际,被广泛运用在实际工程中,但其不足之处是评价结果易受主观因素影响,且越是复杂的环境,评价耗时越多.随着研究工作的深入,涌现出距离判别法(宫凤强等,2007)、可拓学法(胡建华等,2012;凡奥奇等,2024)和TOPSIS法(胡建华等,2012)等评价方法.这些方法在一定程度上避免了评价过程中的主观性,评价精度进一步提高,但仍存在数据样本不足、计算过程冗长和评价模型普适性低等问题.综上所述,岩体质量评价方法一直在推陈出新,但尚有提升空间.随着地下工程的深度不断增加,以及智能化时代的来临,岩体质量评价方法有待进一步发展,如何更加客观、准确且高效地进行岩体质量评价是一个亟待解决的问题. ...
基于属性数学理论的岩体质量分级方法
1
2008
... 岩体质量评价是各类地下工程设计与施工的重要环节之一.在地下工程开发时,工程岩体具有复杂多变的特性,岩体质量分级能体现岩体的物理力学性质,为工程建设的结构参数优化及施工设计提供依据(蔡美峰等,2002;文畅平,2008;赵星光等,2010;沙鹏等,2020;张钦礼等,2021).目前国内外学者对岩体质量评价进行了诸多研究,主要有单因素评价方法(Deere et al.,1966;Li et al.,2004;王明耀等,2022)和多因素评价方法(Palmstrom et al.,2006;贾明涛等,2010;邬爱清等,2014).单因素评价方法虽然简单,但过于片面,取值往往存在模糊性和随机性,忽略了地下工程的复杂性,导致评价结果与实际情况之间相差较大.多因素评价方法综合考虑多项指标,评价结果更接近实际,被广泛运用在实际工程中,但其不足之处是评价结果易受主观因素影响,且越是复杂的环境,评价耗时越多.随着研究工作的深入,涌现出距离判别法(宫凤强等,2007)、可拓学法(胡建华等,2012;凡奥奇等,2024)和TOPSIS法(胡建华等,2012)等评价方法.这些方法在一定程度上避免了评价过程中的主观性,评价精度进一步提高,但仍存在数据样本不足、计算过程冗长和评价模型普适性低等问题.综上所述,岩体质量评价方法一直在推陈出新,但尚有提升空间.随着地下工程的深度不断增加,以及智能化时代的来临,岩体质量评价方法有待进一步发展,如何更加客观、准确且高效地进行岩体质量评价是一个亟待解决的问题. ...
基于岩体质量指标BQ的岩质边坡工程岩体分级方法
3
2014
... 岩体质量评价是各类地下工程设计与施工的重要环节之一.在地下工程开发时,工程岩体具有复杂多变的特性,岩体质量分级能体现岩体的物理力学性质,为工程建设的结构参数优化及施工设计提供依据(蔡美峰等,2002;文畅平,2008;赵星光等,2010;沙鹏等,2020;张钦礼等,2021).目前国内外学者对岩体质量评价进行了诸多研究,主要有单因素评价方法(Deere et al.,1966;Li et al.,2004;王明耀等,2022)和多因素评价方法(Palmstrom et al.,2006;贾明涛等,2010;邬爱清等,2014).单因素评价方法虽然简单,但过于片面,取值往往存在模糊性和随机性,忽略了地下工程的复杂性,导致评价结果与实际情况之间相差较大.多因素评价方法综合考虑多项指标,评价结果更接近实际,被广泛运用在实际工程中,但其不足之处是评价结果易受主观因素影响,且越是复杂的环境,评价耗时越多.随着研究工作的深入,涌现出距离判别法(宫凤强等,2007)、可拓学法(胡建华等,2012;凡奥奇等,2024)和TOPSIS法(胡建华等,2012)等评价方法.这些方法在一定程度上避免了评价过程中的主观性,评价精度进一步提高,但仍存在数据样本不足、计算过程冗长和评价模型普适性低等问题.综上所述,岩体质量评价方法一直在推陈出新,但尚有提升空间.随着地下工程的深度不断增加,以及智能化时代的来临,岩体质量评价方法有待进一步发展,如何更加客观、准确且高效地进行岩体质量评价是一个亟待解决的问题. ...
... 影响岩体质量等级的因素有很多(蔡美峰等,2002).不同学者在研究岩体质量分级时所选取的指标有所不同,各指标之间不是简单的线性关系.查阅相关文献,结合国内外工程经验,主要依据蔡广奎(2001)对于围岩分类参数的分析选取了岩体质量指标RQD(X1)、单轴饱和抗压强度(X2)、岩体完整性系数(X3)、结构面强度系数(X4)和地下渗水量(X5)5个参数作为岩体质量的评价指标.这些指标易获取,且基本反映了岩体自身岩性、地质构造影响和岩体结构等性质,众多学者采用上述指标对岩体质量评价方法进行了研究或对部分指标参数进行了相关分析(Palmstrom et al.,2006;宫凤强等,2007;贾明涛等,2010;胡建华等,2012;邬爱清等,2014).依据相关文献(李强,2002;赖永标等,2006;宫凤强等,2007;胡建华等,2012;邬爱清等,2014),基于《工程岩体分级标准》(中华人民共和国水利部,2014),将岩体质量划分为5个等级:Ⅰ(稳定)、Ⅱ(较稳定)、Ⅲ(基本稳定)、Ⅳ(不稳定)和Ⅴ(极不稳定),分级标准详见表1. ...
... ;邬爱清等,2014),基于《工程岩体分级标准》(中华人民共和国水利部,2014),将岩体质量划分为5个等级:Ⅰ(稳定)、Ⅱ(较稳定)、Ⅲ(基本稳定)、Ⅳ(不稳定)和Ⅴ(极不稳定),分级标准详见表1. ...
基于改进随机森林的苹果分类系统设计
1
2023
... 随着计算机科学的快速发展,BP人工神经网络(李强,2002)、支持向量机(SVM)(赖永标等,2006)和随机森林(RF)(Breiman,2001)等方法已被广泛应用于处理现实问题.其中,随机森林能够有效处理高维小样本数据间的复杂关系,已被广泛运用于餐饮(鞠冠章等,2022)、医疗(韩港飞等,2023)和农业(吴静,2023)等领域,但在地下工程领域的运用较少.采用计算机进行岩体质量评价,可在一定程度上提高评价效率,同时避免主观因素的影响,因此考虑将随机森林运用于岩体质量评价以弥补传统岩体质量评价方法的缺陷.同时,其他学者在研究过程中发现随机森林具备进一步优化的空间(Zhou et al.,2020),而白鲸优化(BWO)是2022年底提出的一种新的群智能优化方法,在众多群智能优化方法的性能测试中表现优异(Zhong et al.,2022).因此,本文尝试使用白鲸优化随机森林,并将优化后的随机森林用于构建岩体质量评价模型,引用工程实例数据验证模型的可行性. ...
绿色开采的理念与技术框架
1
2007
... 从已有文献(许家林等,2007;邱道宏等,2008;唐海等,2011;胡建华等,2021)和实际工程中搜集多个地区实测的131组地下工程岩体数据,建立了本文研究所需的数据库.其中,从文献中搜集的数据均为文献作者从相应项目中获取的真实数据,本文作者基于所承担的项目通过现场试验获取数据,对整个数据库进行了补充,数据库中每组评价参数对应的评价结果均来自对应的项目报告,在本文中被视为真实值.将数据库按7∶3的比例划分为训练集和测试集,用于岩体质量评价模型的训练构建及验证分析.模型构建过程完全依托于训练集,未接触过测试集数据,因此通过测试集对模型进行测试时,模型仅根据构建过程中训练出来的内生逻辑对测试集的输入参数进行预测,将模型预测值与测试集中的真实值进行对比即可评判其准确性,地下工程岩体数据库(部分)见表2. ...
基于Mamdani FIS模型及RMR法的岩体质量分级研究
1
2021
... 岩体质量评价是各类地下工程设计与施工的重要环节之一.在地下工程开发时,工程岩体具有复杂多变的特性,岩体质量分级能体现岩体的物理力学性质,为工程建设的结构参数优化及施工设计提供依据(蔡美峰等,2002;文畅平,2008;赵星光等,2010;沙鹏等,2020;张钦礼等,2021).目前国内外学者对岩体质量评价进行了诸多研究,主要有单因素评价方法(Deere et al.,1966;Li et al.,2004;王明耀等,2022)和多因素评价方法(Palmstrom et al.,2006;贾明涛等,2010;邬爱清等,2014).单因素评价方法虽然简单,但过于片面,取值往往存在模糊性和随机性,忽略了地下工程的复杂性,导致评价结果与实际情况之间相差较大.多因素评价方法综合考虑多项指标,评价结果更接近实际,被广泛运用在实际工程中,但其不足之处是评价结果易受主观因素影响,且越是复杂的环境,评价耗时越多.随着研究工作的深入,涌现出距离判别法(宫凤强等,2007)、可拓学法(胡建华等,2012;凡奥奇等,2024)和TOPSIS法(胡建华等,2012)等评价方法.这些方法在一定程度上避免了评价过程中的主观性,评价精度进一步提高,但仍存在数据样本不足、计算过程冗长和评价模型普适性低等问题.综上所述,岩体质量评价方法一直在推陈出新,但尚有提升空间.随着地下工程的深度不断增加,以及智能化时代的来临,岩体质量评价方法有待进一步发展,如何更加客观、准确且高效地进行岩体质量评价是一个亟待解决的问题. ...
剪胀对地下工程岩体位移的影响——以加拿大Donkin-Morien隧道为例
1
2010
... 岩体质量评价是各类地下工程设计与施工的重要环节之一.在地下工程开发时,工程岩体具有复杂多变的特性,岩体质量分级能体现岩体的物理力学性质,为工程建设的结构参数优化及施工设计提供依据(蔡美峰等,2002;文畅平,2008;赵星光等,2010;沙鹏等,2020;张钦礼等,2021).目前国内外学者对岩体质量评价进行了诸多研究,主要有单因素评价方法(Deere et al.,1966;Li et al.,2004;王明耀等,2022)和多因素评价方法(Palmstrom et al.,2006;贾明涛等,2010;邬爱清等,2014).单因素评价方法虽然简单,但过于片面,取值往往存在模糊性和随机性,忽略了地下工程的复杂性,导致评价结果与实际情况之间相差较大.多因素评价方法综合考虑多项指标,评价结果更接近实际,被广泛运用在实际工程中,但其不足之处是评价结果易受主观因素影响,且越是复杂的环境,评价耗时越多.随着研究工作的深入,涌现出距离判别法(宫凤强等,2007)、可拓学法(胡建华等,2012;凡奥奇等,2024)和TOPSIS法(胡建华等,2012)等评价方法.这些方法在一定程度上避免了评价过程中的主观性,评价精度进一步提高,但仍存在数据样本不足、计算过程冗长和评价模型普适性低等问题.综上所述,岩体质量评价方法一直在推陈出新,但尚有提升空间.随着地下工程的深度不断增加,以及智能化时代的来临,岩体质量评价方法有待进一步发展,如何更加客观、准确且高效地进行岩体质量评价是一个亟待解决的问题. ...
1
2014
... 影响岩体质量等级的因素有很多(蔡美峰等,2002).不同学者在研究岩体质量分级时所选取的指标有所不同,各指标之间不是简单的线性关系.查阅相关文献,结合国内外工程经验,主要依据蔡广奎(2001)对于围岩分类参数的分析选取了岩体质量指标RQD(X1)、单轴饱和抗压强度(X2)、岩体完整性系数(X3)、结构面强度系数(X4)和地下渗水量(X5)5个参数作为岩体质量的评价指标.这些指标易获取,且基本反映了岩体自身岩性、地质构造影响和岩体结构等性质,众多学者采用上述指标对岩体质量评价方法进行了研究或对部分指标参数进行了相关分析(Palmstrom et al.,2006;宫凤强等,2007;贾明涛等,2010;胡建华等,2012;邬爱清等,2014).依据相关文献(李强,2002;赖永标等,2006;宫凤强等,2007;胡建华等,2012;邬爱清等,2014),基于《工程岩体分级标准》(中华人民共和国水利部,2014),将岩体质量划分为5个等级:Ⅰ(稳定)、Ⅱ(较稳定)、Ⅲ(基本稳定)、Ⅳ(不稳定)和Ⅴ(极不稳定),分级标准详见表1. ...







 甘公网安备 62010202000672号
甘公网安备 62010202000672号