岩体爆破开挖在水利建设、隧道交通、矿山开采、市政及军事工程等领域有着非常广泛的应用(张华等,2010),岩体的压碎区范围、冲击波峰值压力均与岩体的不耦合装药结构有关,合理的装药结构能够有效提升炸药的能量利用率(刘云川等,2009)。在实际爆破作业中,炮孔大多是水平或竖向倾斜的,在重力影响下炸药会紧贴炮孔某一侧,形成的偏心不耦合装药结构会对炮孔壁不同方向上需要保护的岩石造成不同程度的损伤甚至开裂,导致超欠挖现象,影响预留岩体的稳定性(宗琦等,2019;Wang et al.,2021)。因此,研究偏心不耦合装药结构岩体爆破动力响应及损伤演化分布在实际工程中具有一定的现实意义。
不耦合装药结构可以降低冲击波峰值压力(梁为民等,2012),提高爆破效率。随着不耦合系数的增大,岩石的损伤因子(表征损伤程度)呈现幂指数衰减(潘强等,2019),而压力增大倍数呈线性增长(叶志伟等,2021)。不耦合偏心装药结构条件下,岩体的损伤分布形态呈明显的非对称性(杨仁树等,2020)。不耦合系数的大小对岩石的爆破效果和裂纹扩展形态均有影响。以往研究表明,在不耦合系数为1.67~2.00之间时爆破效果最佳(徐颖等,2002;Song et al.,2019)。不耦合系数为1.2~2.0时,裂纹扩展的最大长度、炮孔孔壁应力峰值、粉碎区和裂隙区半径均随不耦合系数的增大而逐渐减小(陈啸林等,2023),且裂纹尖端处应力增大易使岩体产生轴向延伸(梁瑞等,2019)。另外,耦合介质对岩石的破坏程度具有显著影响,空气不耦合装药结构的爆压削峰作用是水不耦合装药结构的2倍以上(范勇等,2024),水耦合的最大裂缝长度是空气耦合的6倍以上(Zhu et al.,2007)。此外,爆破地震效率随着炸药装药量和堵药长度的增加而增大(Xia et al.,2018),地震波强度随传播距离的增大呈幂函数衰减(郭学彬等,2006;姜鹏飞等,2009)。
由此可见,以往研究主要讨论了同心不耦合装药爆破结构及对裂纹扩展的研究,而对偏心不耦合装药结构的研究较少。为了研究偏心不耦合装药结构对岩体爆破损伤的影响,在前人研究基础上,基于RHT本构模型,采用初始体积分数法建立不同工况模型,对岩体的动力响应以及损伤演化进行模拟计算和数值分析。
1 模型构建和材料参数设定
1.1 数值模型构建
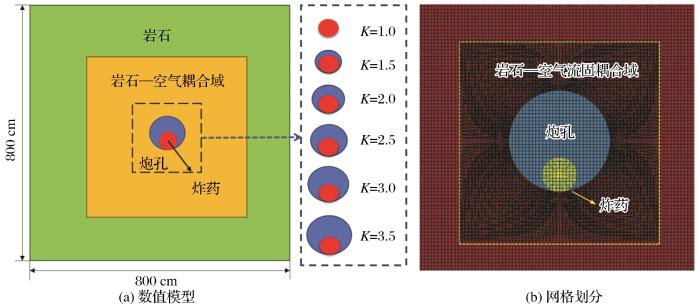
利用ANSYS/LS-DYNA有限元软件对6种不耦合偏心装药情况下的单孔爆破模型进行数值计算,并对不耦合装药结构引起的岩体爆破损伤及能量特性进行研究。模型尺寸为800 cm×800 cm×0.1 cm,岩体类型为花岗岩,不耦合系数K分别取1.0、1.5、2.0、2.5、3.0和3.5。炸药半径取20 cm,炮孔直径根据不耦合系数K确定。在建模过程中,岩体选用Lagrange算法,炸药和空气采用ALE算法,模型采用自由边界条件。图1所示为数值模型及网格划分示意图。
图1
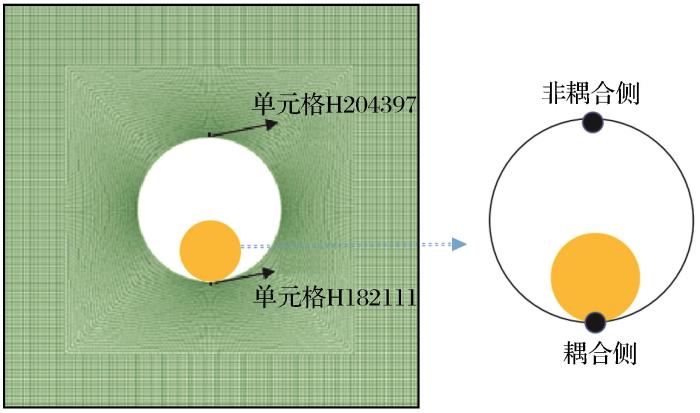
为了探究偏心系数对岩体爆破效果的影响,对炮孔近区耦合侧和非耦合侧单元提取监测点,耦合侧为单元格H204397,非耦合侧为单元格H182111,图2所示为监测点示意图。
图2
1.2 材料参数设定
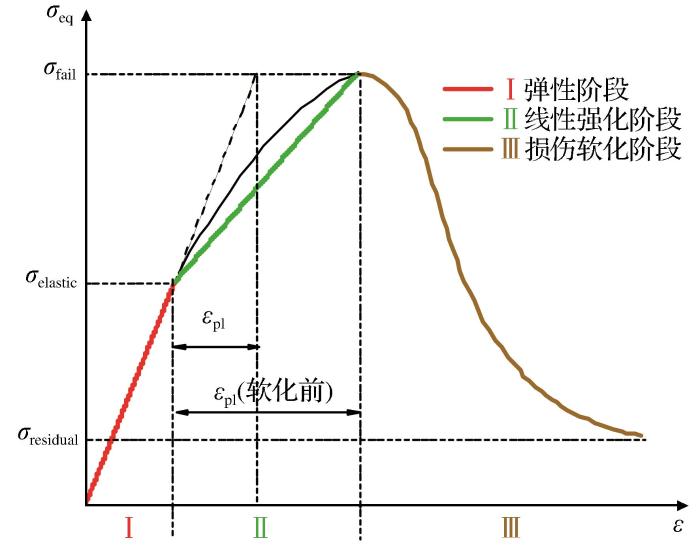
偏应变与偏应力之间的关系如图3所示,本构模型有弹性阶段(σeq≤σelastic)、线性强化阶段(σelastic<σeq<σfail)和损伤软化阶段(σeq>σfail)。
图3
RHT模型的失效面方程为
式中:
其中:
式中:
RHT模型弹性极限面的方程为
RHT模型的残余强度
式中:
为了能够更清晰地反映岩体的应变与失效、拉压损伤等现象,数值模拟时岩石选用RHT本构模型,材料类型为272号 *MAT-RHT,RHT模型的参数由Tawadrous校准(Tawadrous,2010),详细参数如表1所示。其中,岩体初始密度均为2 660 kg/m3;剪切模量为17 GPa;抗压强度fc为150 MPa;
表1 RHT模型参数
Table 1
| 参数 | 数值 | 参数 | 数值 | 参数 | 数值 |
|---|---|---|---|---|---|
| ρ/(kg·m-3) | 2 660 | B1 | 1.22 | B* | 1.6 |
| SHEAR/GPa | 17 | B2 | 1.22 | GC* | 0.4 |
| 150 | Bq | 0.0105 | GT* | 0.7 | |
| A | 2.50 | T1/GPa | 43.87 | M | 0.85 |
| N | 0.85 | T2 | 0 | Q2,0 | 0.685 |
| n | 3 | D1 | 0.04 | AF | 1.62 |
| A1/GPa | 43.87 | D2 | 1 | NF | 0.6 |
| A2/GPa | 49.40 | Pl/MPa | 600 | NP | 4 |
| A3/GPa | 11.62 | Pc/MPa | 133 | ALPHA | 1.10 |
式中:
2 偏心装药条件下岩体动力响应分析
2.1 有效应力分析
在动力载荷作用下,岩体的损伤和破裂发展形式依次为弹性变形、塑性变形、裂隙变形和断裂损伤。损伤分区分别表示为岩石粉碎区、裂隙区和弹性振动区。一旦应力值超过岩体屈服强度,岩体将发生塑性形变,而岩体质点的有效应力能够准确表征其弹性以及弹塑性状态下的力学行为。有效应力不仅考虑了中间主应力和静水压力等对屈服破坏的影响,而且反映了剪应力大小和屈服与破坏之间的非线性关系。有效应力计算公式为
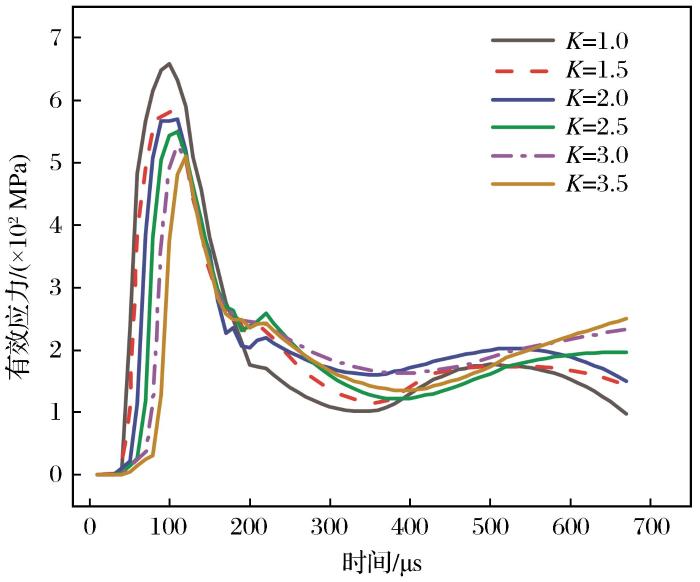
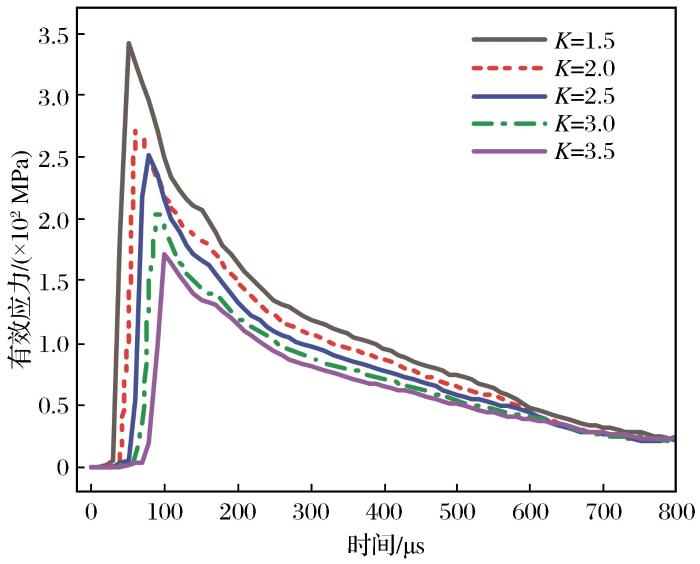
图4
图5
由图4和图5可知,当时间为0~100 μs时爆炸产生的冲击波作用于岩体,使岩体发生粉碎致使耦合侧与非耦合侧有效应力骤增。当K=1.0时,耦合侧有效应力峰值在100 μs左右达到659 MPa,非耦合侧有效应力峰值为342 MPa。分析其原因是因为不耦合装药结构存在压缩性较强的空气层,产生的缓冲作用会降低冲击载荷强度,延迟载荷到达孔壁的时间,致使非耦合侧所受到的压力较耦合侧小得多,随着不耦合系数的增大,有效应力峰值逐渐减小。随后,冲击波衰减变为应力波,有效应力在达到应力峰值后急剧下降并在200 μs后趋于平缓。根据能量守恒定律,炸药起爆能量相同时不耦合系数K越大则炮孔越大,其内部爆轰压力将会减小,爆生气体转化为聚能射流的动能越小,有效应力峰值也会减小。根据上述分析,偏心不耦合装药孔壁压力分布非常不均匀,这种不均匀的孔壁压力将会对炮孔周围的岩体损伤分布特征产生明显影响。
2.2 受载岩体速度分析
图6
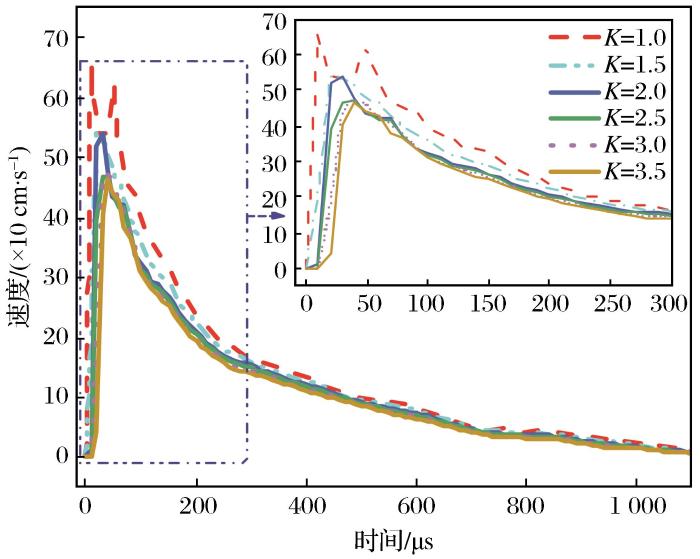
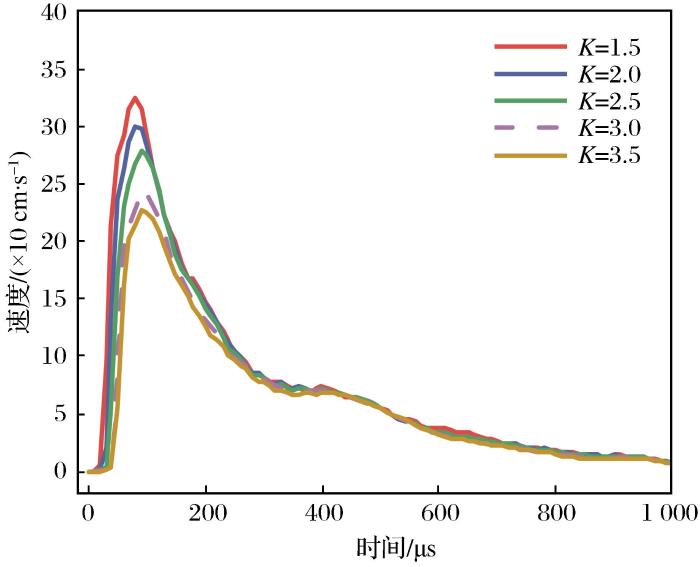
图7
由图6和图7可知,随着时间的推移,耦合侧与非耦合侧质点振动速度均呈先增加后减小的趋势。在冲击波作用下,岩体近区粉碎区振动速度很高,随后在爆生气体作用下推动裂纹扩展,使得振动速度进一步出现峰值。值得注意的是,耦合侧质点振动速度较非耦合侧更快达到峰值,耦合侧质点振动速度峰值集中在50 μs左右,而非耦合侧质点振动速度峰值集中在100 μs左右,其主要原因是采用不耦合装药时,炸药爆炸产生的能量从非耦合侧的空气传递至岩石的过程中能量发生损耗,故耦合侧振动速度大于非耦合侧。随着不耦合系数K的增大,耦合侧与非耦合侧岩体质点峰值速度均逐渐减小,耦合侧不耦合系数K为1.0、1.5、2.5和3.5时,岩体质点振动速度峰值分别为655,532,468,464 cm/s;非耦合侧不耦合系数K为1.5、2.0和3.5时,岩体质点振动速度峰值分别为324,298,225 cm/s。
2.3 爆炸地震波能量影响分析
爆炸是一种瞬态过程,所产生的能量在裂隙区锐减,冲击波转化为应力波,当应力波波阵面能量小于岩石抗断裂破坏能量时,就会产生地震波。
根据Sanchidrián et al.(2007)提出的地震波能量计算公式:
式中:
提取耦合侧和非耦合侧x、y方向的速度,并将其数值代入
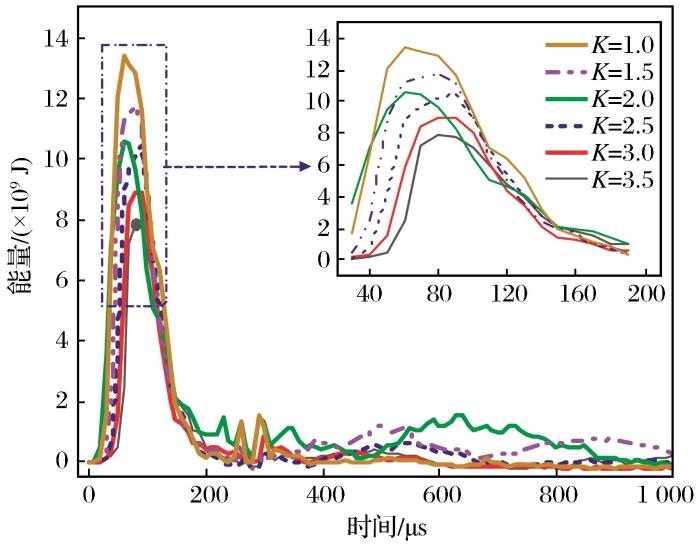
如图8所示,在0~80 μs范围内炸药爆炸产生的能量主要为冲击波能,此时各工况条件下能量达到峰值,冲击波能消耗在粉碎岩体及形成初始裂隙的过程中。随后,在爆生气体的作用下岩石的初始裂纹向外扩张,爆生气体能耗散在裂纹扩展及岩石抛掷的过程中。200 μs以后,爆生气体能降低,冲击波能量衰减转为应力波,应力波逐渐衰减为地震波,爆破地震波处于爆炸远区,只能引起岩石的弹性形变,地震波能量趋于稳定。值得注意的是,当不耦合系数K=1.0时地震波能量峰值达到最大值(13.9×109 J),且能量峰值随着不耦合系数K的增大而减小,即在实际工程中,增大不耦合系数可以降低爆破地震波的强度,减小爆破地震波所带来的危害。
图8
图8
不同工况下地震波能量—时间曲线
Fig.8
Seismic wave energy-time curves under different working conditions
3 不耦合装药条件下岩体损伤演化结果
3.1 受载岩体损伤演化结果分析
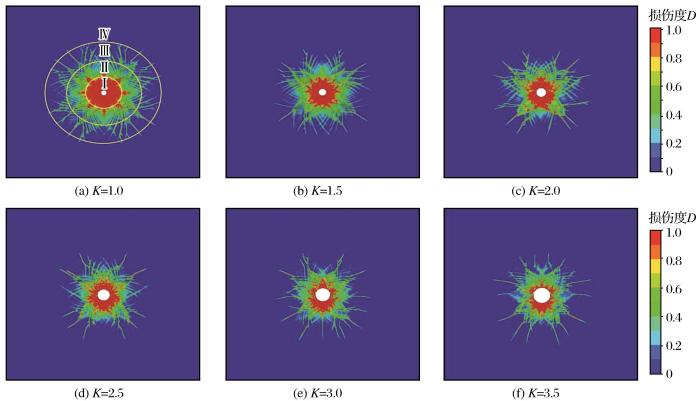
岩体损伤和裂隙发展是由爆破过程中爆破荷载产生的压应力、拉应力以及爆生气体对岩体的气楔共同作用的结果,粉碎区岩体破坏主要以压应力方式呈现,环向裂隙区岩体破坏主要以拉应力方式呈现。为了分析偏心装药不耦合系数对岩体爆破损伤演化的影响,研究t=1 000 μs时刻各工况条件下不耦合系数所对应的损伤云图(图9)。
图9
图9
t=1 000 µs时刻不同工况下岩体损伤云图
Fig.9
Damage cloud images of rock mass under different working conditions at t=1 000 μs
如图9所示,Ⅰ区为爆炸粉碎区,Ⅱ区为密集裂隙区,Ⅲ区为稀疏裂隙区,Ⅳ区为弹性震动区。当不耦合系数K=1.0时,炮孔周围粉碎区面积分布均匀。由于偏心不耦合爆破周围损伤分布存在明显的偏心效应,非耦合侧粉碎区面积和损伤破坏范围较耦合侧粉碎区面积变化较大,且不耦合装药结构炸药与孔壁之间存在间隙,其中的空气对爆炸荷载产生缓冲作用,使爆炸荷载强度降低并延迟荷载作用于孔壁的时间。炸药与孔壁间空气间隔厚度越大,对冲击荷载的缓冲及延迟作用也越强,从而在岩体尺寸、药量和参数相同的情况下,岩体爆破损伤面积随不耦合系数K的增大而逐渐减小。李晓静等(2022)采用数值模拟得到不同不耦合系数K下岩体损伤分布云图与本研究所得结果(图9)基本吻合,进一步验证了本研究模拟结果的准确性。
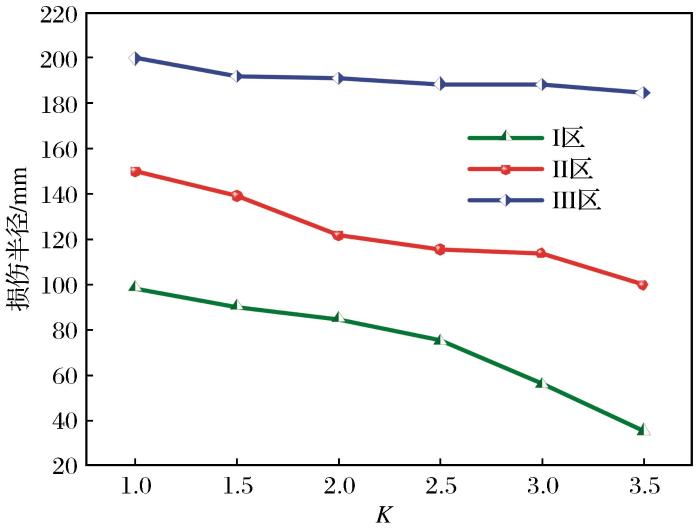
本文装药半径取0.2 m,模拟云图粉碎区半径为0.7~1.2 m,裂隙区半径为1.8~2.7 m,根据前人研究成果,岩石爆破粉碎区半径R与装药半径r的比值为2~7,裂隙区半径R与装药半径r的比值为10~15(黄佑鹏等,2018),本文模拟计算损伤云图符合此研究规律。由此可见,偏心不耦合装药能够更好地破碎开挖侧岩体,减少对预留岩体的损伤,提高炸药能量的利用率。将裂隙区划分为密集裂隙区和稀疏裂隙区,以便开展更细致的研究。如图10所示,各区损伤半径平均值均随着不耦合系数K的增大而减小。粉碎区损伤半径变化率最大,密集裂隙区次之,稀疏裂隙区损伤半径衰减趋势趋于平缓。综上所述,在岩体爆破过程中,不耦合系数K对粉碎区半径的影响远大于对裂隙区损伤半径的影响。
图10
图10
不同工况下岩体损伤半径
Fig.10
Damage radius of rock mass under different working conditions
3.2 不同工况条件下爆心距l与损伤度D的关系
依据现有文献(中国水利学会施工专业委员会爆破学组,1995;胡英国等,2015;潘强等,2019;尹晓玉等,2022),在爆炸前后,当岩石纵波传播速度降低率 η大于10%时,判定岩体受到爆破损伤破坏,岩体损伤度D与岩石纵波传播速度降低率 η 的关系式表示为
将降低率代入
表2 装药半径为0.2 m时不同方法得到的爆破损伤范围
Table 2
| 爆破损伤 范围参数 | 参数获取方法 | 数值 |
|---|---|---|
| 粉碎区R1/m | 公式法: | 0.60~1.47 |
| 经验值:2~7倍装药半径 | 0.4~1.4 | |
| 本文方法 | 0.7~1.2 | |
| 裂隙区R2/m | 公式法: | 1.00~3.87 |
| 经验值:10~15倍装药半径 | 2~3 | |
| 本文方法 | 1.8~2.7 |
为了更准确地描述爆心距l与损伤度D之间的关系,使用Logistic函数对其进行拟合,损伤度D与爆心距l的函数关系表示为
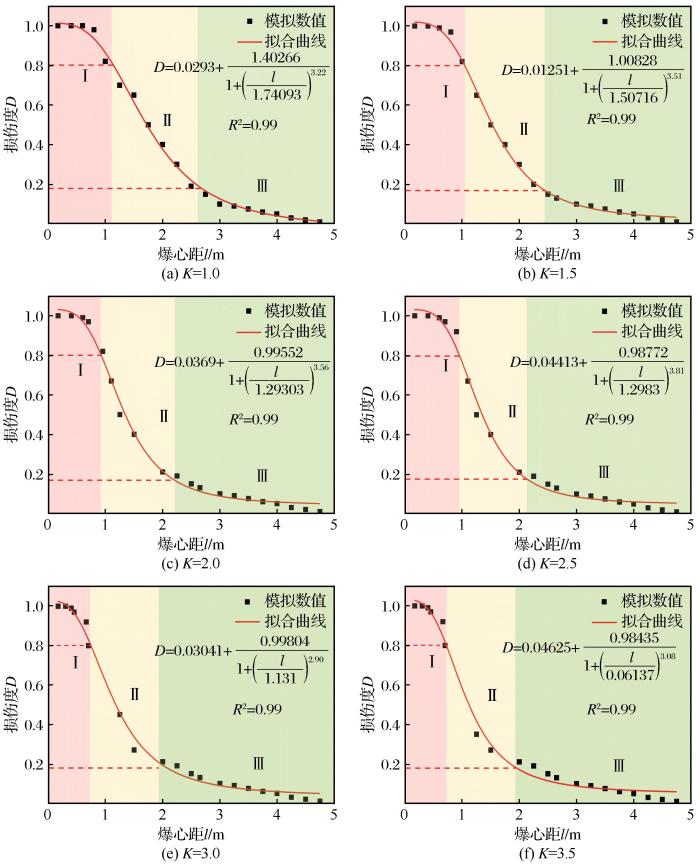
式中:A1、A2和P为相关系数。各点损伤度D与爆心距l关系如图11所示。
图11
图11
爆心距(l)与损伤度(D)之间的变化曲线
Fig.11
Variation curves between burst center distance(l) and damage degree(D)
由图11可见,Ⅰ、Ⅱ和Ⅲ分别表示岩体粉碎区(完全损伤)、裂隙区(部分损伤)和弹性震动区(未损伤)。当不耦合系数K=1.0时,距炮孔中心0~1.1 m范围属于粉碎区,该区域损伤度D>0.80;爆心距范围在1.1~2.7 m之间时为裂隙区,该区域损伤度0.19<D<0.80;爆心距大于2.7 m后为弹性振动区,此时损伤度D<0.19。由表2可知,理论计算得出粉碎区和裂隙区爆破损伤范围分别为0.60~1.47 m和1.00~3.87 m,由经验值得到爆破损伤范围分别为0.4~1.4 m和2~3 m。通过分析图11中6种不同耦合系数控制下的爆心距 l 与损伤度 D 拟合函数,得出粉碎区平均范围约为1 m,裂隙区平均范围约为2 m,与表2中数值基本吻合,验证了本文模拟结果的准确性。值得注意的是,随着不耦合系数K的增大,装药量和炸药能量逐渐减少,致使冲击波和应力波能量减小,粉碎区和裂隙区范围也逐渐缩小,而弹性振动区范围随之增加,裂隙区拟合曲线斜率逐渐增大。
3.3 炮孔近区峰值振动速度vpp分布
质点峰值振动速度vpp损伤判据理论是一种损伤判断的依据,在实际工况中运用较为广泛,其依据一维弹应力波理论,即:
式中:σt为最大拉应力;c1为岩体中纵波传播速度。本文取不耦合系数K为1.0、2.0和3.0,研究不同不耦合系数工况条件下质点峰值振动速度vpp与爆心距l之间的关系。在炮孔径向方向取20个观测点,各个观测点间距为0.1 m,对其观测点进行监测;然后根据弹应力波理论得出该监测点的峰值振动速度vpp阈值,并绘制峰值振动速度vpp阈值与爆心距l之间的关系曲线,结果如图12所示。
图12
图12
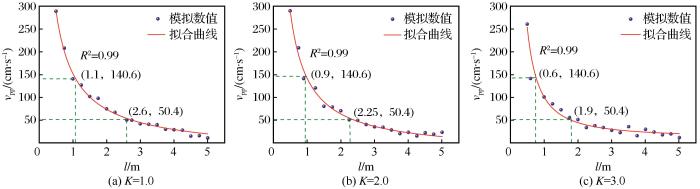
峰值振动速度(vpp)与爆心距(l)之间的关系曲线
Fig.12
Relationship curves between peak vibration velocity(vpp) and blast center distance(l)
由图12可知,3种工况条件下数值拟合度均为0.99,说明其拟合公式能够准确地描述质点峰值振动速度vpp阈值与爆心距l之间的关系。当不耦合系数K=1.0时,爆心距范围在0~1.1 m之间时为粉碎区,vpp峰值达到140.6 cm/s;爆心距l增大至2.6 m左右时属于裂隙区,vpp峰值为50.4 cm/s;当爆心距l >2.6 m时,vpp<50.4 cm/s,此时状态处于弹性振动区。整体来看,3种工况条件下vpp阈值与爆心距变化趋势大致相同,均随爆心距l的增大而减小。值得注意的是,粉碎区vpp峰值随爆心距的增大而迅速减小。随着不耦合系数K的增大,冲击波能量减少,致使粉碎区范围缩小,曲线弯曲程度增大。粉碎区、裂隙区数值范围与图11中数值范围相一致。其他学者得到的岩体爆破近区vpp峰值随爆心距衰减曲线(胡英国等,2015)与本研究所得结果(图12)基本相似,再次验证了本文模拟结果的准确性。图13所示为损伤变量D与vpp的关系曲线。
图13
图13
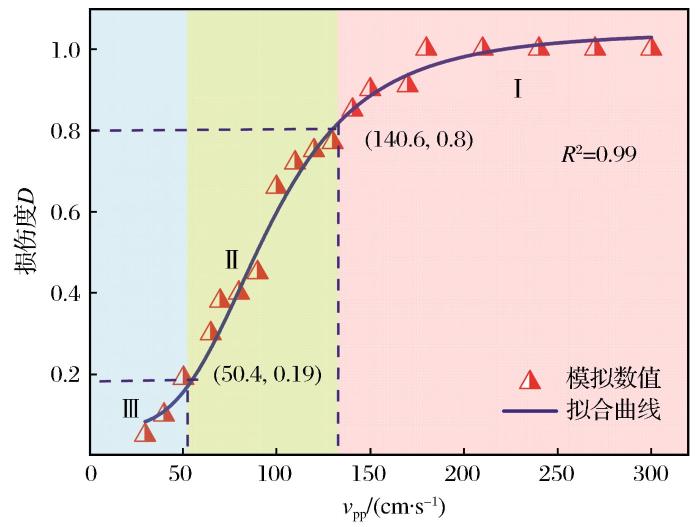
峰值振动速度(vpp)与损伤变量(D)之间的关系曲线
Fig.13
Relationship curves between peak vibration velocity (vpp) and damage variable (D)
4 结论
基于RHT本构关系,通过建立单孔偏心不耦合爆破模型分析了不同工况条件下不耦合系数对岩体的动力响应和岩体爆破损伤演化分布,探究不同不耦合系数K条件下爆心距l与损伤度D、质点振动速度vpp与爆心距l,以及振动速度vpp与损伤度D的关系,得出以下结论:
(1)随着不耦合系数K的增大,有效应力、峰值振动速度、地震波峰值能量、岩体爆破损伤面积和损伤半径平均值均随不耦合系数K的增大而减小。粉碎区损伤半径变化率最大,密集裂隙区次之,稀疏裂隙区损伤半径衰减趋势趋于平缓。不耦合系数K对粉碎区半径的影响远大于对裂隙区损伤半径的影响。
(2)对不同工况条件下爆心距l与振动速度vpp、岩体损伤程度D的关系进行分析,理论计算得出粉碎区和裂隙区爆破损伤半径范围分别为0.60~1.47 m和1.00~3.87 m,经验值得出爆破损伤范围分别为0.4~1.4 m和2~3 m。本文得到不同不耦合系数K工况条件下的粉碎区半径爆心距平均范围约为1 m、裂隙区约为2 m,与理论经验数值基本吻合。
(3)研究岩体损伤程度D与振动速度vpp的对应关系,发现随着vpp的增加,岩体损伤程度从0开始增加至0.8左右,然后随着vpp增大速度逐渐放缓。当vpp<50.4 cm/s时,D<0.19,岩体出现轻微损伤状况;当50.4 cm/s<vpp<140.6 cm/s时,0.19<D<0.80,岩体进入裂隙区,出现部分损伤;当vpp>140.6 cm/s时,岩体损伤度D>0.80,岩体将完全损伤。
http://www.goldsci.ac.cn/article/2024/1005-2518/1005-2518-2024-32-2-306.shtml
参考文献
Study on Dynamic Response and Blasting Characteristics of Deep Rock Blasting
[D].
Relationship between crack extension and uncoupled charging coefficient in deep rock blasting
[J].
Calculation of rock crushed circle and fracture circle by column charge blasting
[J].
The effect of burst pressure peak elimination by radial uncoupled charge and its effect on the range of rock fracture
[J].
On the attenuation characteristics of blasting seismic waves during propagation
[J].
Determination of reasonable width of narrow coal pillar based on the third invariant of bias stress
[J].
Determination of peak vibration velocity of critical damage plasmas in the near zone of rock blasting
[J].
Simulation analysis of rock blasting damage range and damage distribution characteristics
[J].
Numerical analysis of the effect of uncoupled charge blasting on hard rock stress field
[J].
Numerical simulation of blasting damage distribution characteristics of eccentric uncoupled charge
[J].
Characteristics of blasting damage to rock in the proximal zone of hydropower engineering slope gun holes
[J].
Research on blasting crack extension in slope excavation based on stress and velocity time course analysis
[J].
Effect of uncoupled charge structure on rock blasting
[J].
An energy method for calculate borehole pressure under decoupled charging
[J].
Characterization of rock damage distribution in single-hole uncoupled charge blasting
[J].
Analysis of the coupling between laminar distribution and blasting damage based on RHT model
[J].
Energy components in rock blasting
[J].
Study on the decoupled charge effect in deep-hole cumulative blasting of coal seam
[J].
Hard Rocks Under High Strain-rate Loading
[D].
Study on eccentric uncoupled blasting effect of cutting seam pipe
[J].
Role of the second and third invariants of the bias stress tensor in plastic processing
[J].
Experimental study on the seismic efficiency of rock blasting and its influencing factors
[J].
Experimental study on the control of blasting cracks by charge uncoupling coefficient
[J].
A fractal study on blasting damage of an eccentric decouple charge structure
[J].
Calculation method of peak pressure of hole wall for blasting with small uncoupling coefficient charge
[J].
Analysis of the impact of blasting construction on the stability of tunnel surrounding rock
[J].
Experimental studies on blasting vibration velocity attenuation law in deep open-pit mining
[J].
Numerical investigation of blasting-induced crack initiation and propagation in rocks
[J].
Numerical simulation of pressure and damage effects on the hole wall of eccentric uncoupled charge
[J].
深层岩体爆破动力响应和爆破特性研究
[D].
深部岩石爆破裂纹扩展与不耦合装药系数的关系
[J].
柱状装药爆破岩石破碎圈和断裂圈计算
[J].
径向不耦合装药爆压消峰作用及其对岩石破裂范围影响
[J].
论爆破地震波在传播过程中的衰减特性
[J].
基于偏应力第三不变量的窄煤柱合理宽度确定
[J].
岩体爆破近区临界损伤质点峰值震动速度的确定
[J].
岩石爆破损伤范围及损伤分布特征模拟分析
[J].
不耦合装药爆破对硬岩应力场影响的数值分析
[J].
偏心不耦合装药爆破损伤分布特征数值模拟
[J].
水电工程边坡炮孔近区岩体爆破损伤特性
[J].
基于应力与速度时程分析的边坡开挖爆破裂纹扩展研究
[J].
不耦合装药结构对岩石爆破的影响
[J].
不耦合装药条件下炮孔初始压力计算的能量方法
[J].
单孔不耦合装药爆破的岩体损伤分布特征研究
[J].
基于RHT模型的层理分布与爆破损伤关联耦合性分析
[J].
偏应力张量第二及第三不变量在塑性加工中的作用
[J].
装药不耦合系数对爆破裂纹控制的试验研究
[J].
不耦合偏心装药结构爆破损伤破坏的分形研究
[J].
小不耦合系数装药爆破孔壁压力峰值计算方法
[J].
爆破施工对隧道围岩的稳定性影响分析
[J].
深凹露天爆破震动速度衰减规律实验研究
[J].
偏心不耦合装药孔壁压力与损伤效应数值模拟
[J].





 甘公网安备 62010202000672号
甘公网安备 62010202000672号