基于混合整数规划的风流两步骤调控优化方法

doi:10.11872/j.issn.1005-2518.2024.02.0014

基于混合整数规划的风流两步骤调控优化方法

钟德云^,¹^,², 文历学^,², 王李管¹^,²

1.长沙迪迈科技股份有限公司，湖南长沙 410221

2.中南大学资源与安全工程学院，湖南长沙 410083

Two-step Optimization Method for Airflow Control Based on Mixed Integer Programming

ZHONG Deyun^,¹^,², WEN Lixue^,², WANG Liguan¹^,²

1.Changsha Dimine Co. , Ltd. , Changsha 410221, Hunan, China

2.School of Resources and Safety Engineering, Central South University, Changsha 410083, Hunan, China

通讯作者: 文历学（2000-），男，湖南衡阳人，硕士研究生，从事智能通风研究工作。225512108@csu.edu.cn

收稿日期: 2024-01-02 修回日期: 2024-04-01

基金资助:

国家重点研发计划项目“超大型深井矿山高效绿色开采技术与智能装备”. 2022YFC2904105

Received: 2024-01-02 Revised: 2024-04-01

作者简介 About authors

钟德云（1990-），男，福建长汀人，博士后，从事智能通风和地质建模研究工作deyizhiyun@163.com , E-mail：deyizhiyun@163.com

摘要

实现按需通风是当前矿井智能通风系统推进建设过程的核心技术问题。为解决矿井通风网络优化调控非线性模型求解困难的问题，在改进两步骤通风优化方法的基础上，提出了一种基于混合整数规划的风流两步骤调控优化数学模型。该模型以通风能耗最小、调节点个数最少和调节点位置最佳等为目标，是一种多目标线性规划模型，其求解结果更加符合矿山实际调控需求。改进的两步骤通风优化方法具有以下优点：通过引入混合整数规划方法，该模型可以对调节方案的调节点个数和调节方式进行约束；通过引入分支调节级数，该模型可以根据井下实际情况对调节方案的位置进行约束，从而提高了通风网络优化调节方案的灵活性；此外，通过多次求解风量分配对应调控方案的方式，该模型既可以得到近似满足风量未知调控模型的求解方案，也可以避免非线性模型求解不收敛的问题。通过构建矿井通风优化调控计算实例模型，在通风网络模型进行分风计算的基础上验证了通风网络模型调控的可靠性。

关键词： 矿井通风 ; 通风调节 ; 通风优化 ; 风流调节 ; 两步法 ; 混合整数规划

Abstract

Intelligent mining is an important direction for the future development of the mining industry.The construction of mine intelligent ventilation system is a key part of promoting the digital and intelligent development of mines.Under the current background of energy conservation and emission reduction，the ways of digital and information technology to achieve low-carbon mining，efficient utilization and intelligent control of non-ferrous metal resources，is the important technical guarantee to achieve the strategy of “carbon peaking and carbon neutrality”.The key to realize the high-efficiency utilization of non-ferrous metal resources is to adopt the intelligent ventilation technology to reduce the energy consumption.In the current process of pro-moting the construction of intelligent mine ventilation system，a common hot and difficult issue is to realize the optimal regulation of airflow of mine ventilation system under the condition of ventilation on-demand.The ventilation optimization regulation of intelligent ventilation system requires that on the premise of satisfying the dynamic ventilation on-demand in different periods，the ventilation optimization theory based on fluid network was adopted to obtain a ventilation optimization regulation scheme that meets the requirements of safety，technology and economic.Then the airflow distribution and air pressure distribution of the ventilation network were adjusted to ensure the safe，reliable，stable and economic operation of the mine ventilation system.In order to solve the problem of difficulty in solving the optimization and regulation model of nonlinear mine ventilation network，based on the basic mathematical model of ventilation network airflow regulation，the method of airflow control and optimization of ventilation network was analyzed，and the objectives and constraints of the airflow regulation optimization model based on multi-objective mixed integer programming were analyzed.A two-step airflow control optimization mathematical model based on the mixed integer programming method by improving the two-step ventilation optimization method was proposed.The mathematical model is a multi-objective programming linear model with the goals of minimum ventilation energy consumption，minimum number of regulation equipment and optimal position of regulation equipment，so that the solution result of the mathematical model is more in line with the actual regulation needs.The mathematical model can constraint the number and regulating ways of regulation position by introducing the mixed integer programming method，and constraint the position of regulation schemes according to the actual situation of the mine by introducing the regulation level of branches，which improve the flexibility of ventilation regulation optimization schemes.In addition，by solving the corresponding regulation schemes of airflow distribution multiple times，the mathematical model can obtain a solution scheme that approximately satisfies the solution result of regulation mathematical model with unknown airflow，while avoiding the problem of non-convergence in solving nonlinear models.We construct a calculation example for the mine ventilation optimization regulation problem，and verify the reliability of ventilation regulation mathematical model based on the calculation of airflow distribution.

Keywords： mine ventilation ; ventilation regulation ; ventilation optimization ; airflow regulation ; two-step way ; method integer programming

PDF (2090KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

钟德云, 文历学, 王李管. 基于混合整数规划的风流两步骤调控优化方法[J]. 黄金科学技术, 2024, 32(2): 356-365 doi:10.11872/j.issn.1005-2518.2024.02.0014

ZHONG Deyun, WEN Lixue, WANG Liguan. Two-step Optimization Method for Airflow Control Based on Mixed Integer Programming[J]. Gold Science and Technology, 2024, 32(2): 356-365 doi:10.11872/j.issn.1005-2518.2024.02.0014

近年来，智能开采技术的发展促进了智能通风技术的研究，相关学者对智能通风系统开展了大量相关研究（刘剑，2020；卢新明等，2020；周福宝等，2020，2023；王凯等，2023；张景钢等，2023）。矿井通风网络调节的目的是实现矿井智能按需分风（吴新忠等，2021），如何确定复杂通风网络的调节方案是矿井智能通风系统中决策支持的关键技术难题。通风优化调控要求在满足井下不同时期动态按需分风的前提下，采用基于流体网络的通风优化理论获得满足矿山实际安全生产要求、技术合理可靠和经济性能最优的通风优化调控方案，以调整通风网络的风量分配和风压分布状态，确保矿井通风系统安全、可靠、稳定且经济运行。

国内外学者对采用数学规划的方法来求解矿井通风网络优化调控方案进行了大量研究，以获取具有较低通风能耗的最佳调节方案。早期学者对无约束非线性规划的通风调控模型进行了深入研究，以采用共轭梯度法来求解相应模型的最优解。为了移除风量平衡约束条件，Ueng et al.（1984）对矿井通风网络的非线性规划问题进行了分析，基于Wang（1984）提出的有约束非线性规划模型，提出了结合图论构造目标函数的方法。随后，相关学者对通风调控模型的约束构造和非线性求解方法进行了深入研究。Wu et al.（1998）分析了矿井通风网络的运筹学优化方法，提出了2种通风网络风流调控设施位置和调节量大小的数学规划模型。Hu et al.（2003）分析了通风网络非线性全局控制和局部控制的调节方法。近10年来，相关学者开始关注结合通风系统优化设计、通风能耗和调节可靠性等相关的约束构造方法。Acuña et al.（2014）对如何使用数学方法来确定与风机功率成本相关的矿井通风系统的优化设计进行了分析。Sotoudeh et al.（2018）建立了以调节设施数量和通风能耗最小化为目标函数的风量调节优化模型。Chen et al.（2015）以矿井通风网络理论为基础，建立了一种非线性多目标优化数学模型来处理较难的半控制型分风问题。为了提高非线性调控模型的求解效率，相关学者提出了大量智能优化的方法来求解通风网络非线性模型（Gao，2004；Lowndes et al.，2005；Stepanenko et al.，2007；Gao，2011；Kozyrev et al.，2012；Gu et al.，2014；Gao et al.，2018；Liang et al.，2018）。

通风系统风量优化调控的难点在于通风优化模型中的风量变量为非线性变量类型，只要风量未知，在构造数学模型时约束条件和目标函数均会出现非线性项，造成模型求解困难的问题。两步骤通风优化法将风量分配优化和风量调控优化作为2个独立的步骤分别处理：先在按需分风条件下解算通风网络的自然分风结果，再确定自然分风条件下风量调控的优化方案。该方法的主要特点是将风量变量与调节变量相分离，从而极大地降低数学模型的变量规模和求解复杂度。

为了提高通风网络优化调节方案的灵活性，本文结合多目标规划的方法提出了通风网络风量调控优化多目标规划数学模型，使得模型求解结果更加符合矿山实际调节需要。针对非线性模型求解困难的问题，本文在改进两步骤通风优化方法的基础上，提出了一种基于混合整数规划的风流两步骤调控优化数学模型。由于该模型考虑了增能调节的方式，适用于非煤矿井通风系统的优化调控。

1 风量调控优化计算方法

目前，根据混合型分风网络的风量最优分配和风量最优调控的求解方式，成熟的通风网络优化方法通常有2种：全局通风优化法和两步骤通风优化法。

1.1 全局通风优化法

全局通风优化法通过综合考虑风量分配优化和风量调控优化来实现整个通风网络的全局优化。全局通风优化法是通风网络优化调控的常用方法。然而，一般混合型通风网络优化调控的数学模型为非线性、非凸规划模型，涉及待求风量、调节设置位置及相应调节量等决策变量。尽管相关学者基于启发式算法或智能优化算法引入了多种通风网络优化非线性求解方式，但是目前仍然没有高效可靠的数学模型最优解求解方法。因此，全局通风优化法难以处理大规模通风网络的优化调控问题。

1.2 两步骤通风优化法

两步骤通风优化法将复杂的通风网络优化问题分解为风量分配优化和风量调控优化2个子问题，由于这2个子问题都是线性的，从而降低了通风优化问题的求解难度和复杂度。

尽管两步骤通风优化法已经得到了大量应用，但由于2个步骤计算过程具有独立性，该方法仍然存在较大的局限性。由于调节优化是在自然分风计算的基础上进行的，自然分风计算的风量分配结果是唯一确定的，不能像全局通风优化法那样设置一个可以调整的风量上下限约束条件，缺乏足够的调整灵活性。在某些特殊情况下，当基于自然分风计算得到的风量分配结果无法找到合适的调节方案时，应进一步考虑次优风量分配条件下的最优调节方案。即两步骤通风优化法得到的第一步骤风量分配结果不一定能满足第二步骤调节约束条件下的全局最优方案。

2 风量调控目标约束分析

2.1 风量调控目标

（1）最小通风能耗目标

最小通风能耗目标可表示为

m i n z_{1} = ω_{1} \sum_{j = 1}^{N} q_{j} (r_{j} q_{j}^{2} + ∆ h_{j} - h_{N, j})

（1）

式中： $z_{1}$ 为最小通风能耗目标； $ω_{1}$ 为最小通风能耗目标的权重系数； $N$ 为通风网络的分支数； $q_{j}$ 为第 $j$ 条分支的风量； $r_{j}$ 为第 $j$ 条分支的风阻； $∆ h_{j}$ 为第 $j$ 条分支的风压调节值； $h_{r, j}$ 为第 $j$ 条分支的通风阻力， $h_{r, j} = r_{j} q_{j}^{2}$ ； $h_{N, j}$ 为第 $j$ 条分支的自然风压； $h_{r, j}^{'}$ 为第 $j$ 条分支通风阻力的代数和， $h_{r, j}^{'} = h_{r, j} + ∆ h_{j} - h_{N, j}$ 。

（2）最佳调节位置目标

为了量化通风网络中特定调节位置分支的可调节性，可以定义一种分支调节级数（整数类型数值）来表示调节位置约束。本文构造的分支调节级数满足以下特性：

①分支调节级数的默认数值为零，表示该分支为允许任意调节方式的可调分支；

②分支调节级数的绝对值越大，表示该分支越不可调节；

③分支调节级数符号为正且数值越大，表示该分支越不可增阻调节；

④分支调节级数符号为负且数值越小，表示该分支越不可增能调节或降阻调节；

⑤可调分支调节级数的绝对值接近于零，不可调分支调节级数的绝对值趋于一个较大的整数值；

⑥可增阻调节分支调节级数的符号为正，可增能调节分支或可降阻调节分支调节级数的符号为负。

最佳调节位置目标可表示为

m i n z_{2} = ω_{2} \sum_{j = 1}^{N} n_{j, a} |s_{j}|

（2）

式中： $z_{2}$ 为最佳调节位置目标； $ω_{2}$ 为最佳调节位置目标的权重系数； $s_{j}$ 为第 $j$ 条分支的调节级数，调节级数由分支的可调性确定； $n_{j, a}$ 为0-1整型变量，表示是否需要对第 $j$ 条分支进行调节。

对于 $n_{j, a}$ 应满足

n_{j, a} = \{\begin{matrix} 0, 当 |∆ h_{j}| \leq ρ_{j} \\ 1, 当 |∆ h_{j}| > ρ_{j} \end{matrix}

（3）

式中： $∆ h_{j}$ 为第 $j$ 条分支的风压调节值； $ρ_{j}$ 为第 $j$ 条分支允许忽略的调节量（调节因子），满足 $ρ_{j}$ >0。

为了便于求解数学模型，引入 $∆ h_{j}^{'}$ 表示 $∆ h_{j}$ 的绝对值 $|∆ h_{j}|$ 。 $∆ h_{j}^{'}$ 满足以下条件：

\{\begin{matrix} ∆ h_{j}^{'} \geq ∆ h_{j} \\ ∆ h_{j}^{'} \geq - ∆ h_{j} \end{matrix}

（4）

在以上条件的约束下，存在 $∆ h_{j}^{'} \geq 0$ 的隐式约束条件。为了限制 $∆ h_{j}^{'}$ 的大小，采用优先等级法引入一个具有最高优先级的目标约束，以确保 $∆ h_{j}^{'} = |∆ h_{j}|$ 。

m i n z_{0} = ω_{0} ∆ h_{j}^{'} (j = 1,2, \dots, N)

（5）

式中： $z_{0}$ 为限制风压调节值变量的附加目标； $ω_{0}$ 为限制风压调节值变量的权重系数（取一个较大的数值）。

上述附加目标必须得到优先满足，否则会影响0-1整型变量 $n_{j, a}$ 取值的可靠性。0-1整型变量 $n_{j, a}$ 需要满足以下条件：

\{\begin{matrix} |∆ h_{j}| - ρ_{j} \leq n_{m a x, a} n_{j, a} \\ ρ_{j} n_{j, a} \leq |∆ h_{j}| \end{matrix}

（6）

\{\begin{matrix} ∆ h_{j}^{'} - ρ_{j} \leq n_{m a x, a} n_{j, a} \\ ρ_{j} n_{j, a} \leq ∆ h_{j}^{'} \end{matrix}

（7）

式中： $n_{m a x, a}$ 可设置为一个较大的正常量，以确保 $∆ h_{j}^{'} - ρ_{j} \leq n_{m a x, a}$ 。

在以上条件的约束下，0-1整型变量 $n_{j, a}$ 满足 $n_{j, a} = \{\begin{matrix} 0, 当 |∆ h_{j}| \leq ρ_{j} \\ 1, 当 |∆ h_{j}| > ρ_{j} \end{matrix}$ ，此处要求 $ρ_{j}$ >0。

（3）最佳调节方式目标

调节级数考虑了分支对应的调节方式，而最佳调节位置目标没有考虑调节点位置的调节方式。因此，需要进一步构造最佳调节方式目标。

最佳调节位置目标可表示为

m i n z_{3} = ω_{3} (\sum_{j = 1, s_{j} > 0}^{N} n_{j, b} s_{j} - \sum_{j = 1, s_{j} < 0}^{N} n_{j, c} s_{j})

（8）

式中： $z_{3}$ 为最佳调节方式目标； $ω_{3}$ 为最佳调节方式目标的权重系数； $s_{j}$ 为第 $j$ 条分支的调节级数，调节级数由分支的可调性确定； $n_{j, b}$ 表示是否需要对第 $j$ 条分支进行增阻调节； $n_{j, b}$ 满足 $n_{j, b} = \{\begin{matrix} 0, 当 ∆ h_{j} \leq ρ_{j} \\ 1, 当 ∆ h_{j} > ρ_{j} \end{matrix}$ ； $n_{j, c}$ 为是否需要对第 $j$ 条分支进行增能调节或降阻调节； $n_{j, c}$ 满足 $n_{j, c} = \{\begin{matrix} 0, 当 ∆ h_{j} \geq - ρ_{j} \\ 1, 当 ∆ h_{j} < - ρ_{j} \end{matrix}$ ； $∆ h_{j}$ 为第 $j$ 条分支的风压调节值； $ρ_{j}$ 为第 $j$ 条分支允许忽略的调节量（调节因子），满足 $ρ_{j}$ >0。

为了便于求解数学模型，引入混合整数规划方法将 $n_{j, b}$ 定义为0-1整型变量，表示是否需要对第 $j$ 条分支进行增阻调节；将 $n_{j, c}$ 定义为0-1整型变量，表示是否需要对第 $j$ 条分支进行增能调节或降阻调节。

0-1整型变量 $n_{j, b}$ 需要满足以下条件：

\{\begin{matrix} ∆ h_{j} - ρ_{j} \leq n_{m a x, b} n_{j, b} \\ n_{j, b} + n_{j, c} = n_{j, a} \end{matrix}

（9）

式中： $n_{m a x, b}$ 可设置为一个较大的正常量，以确保 $∆ h_{j} - ρ_{j} \leq n_{m a x, b}$ 。

0-1整型变量 $n_{j, c}$ 需要满足以下条件：

\{\begin{matrix} - (∆ h_{j} + ρ_{j}) \leq n_{m a x, c} n_{j, c} \\ n_{j, b} + n_{j, c} = n_{j, a} \end{matrix}

（10）

式中： $n_{m a x, c}$ 可设置为一个较大的正常量，以确保 $- (∆ h_{j} + ρ_{j}) \leq n_{m a x, c}$ 。

（4）最少调节个数目标

在调节级数绝对值总和接近的情况下，应尽量确保调节点个数最少。即除了最优调节位置之外，最优的调节方案还要求风量调控优化模型应尽量减少调节点数目且优先采用增阻调节的方式，以降低通风系统调控成本并简化通风调控设施管理过程。

在对井下通风系统进行实际优化调控时，某条巷道只有调节量达到一定数值时，才会在相应位置安装相应的调节设施或进行调节操作。为了避免较小调节量对调节个数约束的影响，可以设置特定分支无需进行调节的调节因子。

最少调节个数目标可表示为

m i n z_{4} = ω_{4} \sum_{j = 1}^{N} n_{j, a}

（11）

式中： $z_{4}$ 为最少调节个数目标； $ω_{4}$ 为最少调节个数目标的权重系数； $n_{j, a}$ 为是否需要对第 $j$ 条分支进行调节； $n_{j, a}$ 满足 $n_{j, a} = \{\begin{matrix} 0, 当 |∆ h_{j}| \leq ρ_{j} \\ 1, 当 |∆ h_{j}| > ρ_{j} \end{matrix}$ ； $∆ h_{j}$ 为第 $j$ 条分支的风压调节值； $ρ_{j}$ 为第 $j$ 条分支允许忽略的调节量（调节因子），满足 $ρ_{j}$ >0。

2.2 风量调控约束

（1）风压平衡约束条件

通风网络风量调节方案必须满足回路风压平衡条件，即在通风网络中任意回路中各分支风压代数和为零。

\sum_{j = 1}^{N} b_{i j} h_{j} = \sum_{j = 1}^{N} b_{i j} (r_{j} q_{j}^{2} + ∆ h_{j} - h_{f, j} - h_{N, j}) = 0

(i = 1,2, \dots, M)

（12）

式中： $M$ 为通风网络的独立回路数， $M = N - J + 1$ ； $h_{j}$ 为第 $j$ 条分支风压的代数和， $h_{j} = r_{j} q_{j}^{2} + ∆ h_{j} - h_{f, j} - h_{N, j}$ ； $r_{j}$ 为第 $j$ 条分支的风阻； $∆ h_{j}$ 为第 $j$ 条分支的风压调节值； $h_{f, j}$ 为第 $j$ 条分支的风机风压； $h_{N, j}$ 为第 $j$ 条分支的自然风压； $b_{i j}$ 表示分支与回路的关系。其中， $b_{i j}$ 满足以下条件：

b_{i j} = \{\begin{matrix} 0, 当分 支 j 不在 独立 回路 i 内 \\ - 1, 当分 支 j 在独 立回 路 i 内, 且与 回路 反向 \\ 1, 当分 支 j 在独 立回 路 i 内, 且与 回路 同向 \end{matrix}

（2）调节位置约束条件

当第 $j$ 条分支不允许安装调节设施（不可调分支）时，则

∆ h_{j}

=0（13）

值得注意的是，在不影响调节效果的情况下，对于不可调分支，可以设置一个可以忽略的调节容差范围，因此第 $j$ 条分支不允许安装调节设施约束可表示为

- ρ_{j}^{'} \leq ∆ h_{j} \leq ρ_{j} ″

（14）

式中： $ρ_{j}^{'}$ 为第 $j$ 条分支允许忽略的增能或降阻调节量（调节因子），满足 $ρ_{j}^{'}$ >0； $ρ_{j} ″$ 为第 $j$ 条分支允许忽略的增能调节量（调节因子），满足 $ρ_{j} ″$ >0。

（3）调节方式约束条件

第 $j$ 条分支风压调节量约束条件可表示为

∆ h_{j, m i n} \leq ∆ h_{j} \leq ∆ h_{j, m a x}

（15）

式中： $∆ h_{j, m i n}$ 为第 $j$ 条分支可调节风压下限； $∆ h_{j, m a x}$ 为第 $j$ 条分支可调节风压上限。

当第 $j$ 条分支只允许增阻调节约束时，则

∆ h_{j} \geq 0

（16）

当第 $j$ 条分支只允许增能调节（或降阻调节）约束时，则

∆ h_{j} \leq 0

（17）

（4）调节个数约束条件

为了降低通风系统调控成本，简化通风调控设施管理过程，优化模型的调节方案应尽量减少调节点数目。

\sum_{j = 1}^{N} n_{j, a} \leq N_{a}

（18）

式中： $N_{a}$ 为通风网络中允许调节分支的个数； $n_{j, a}$ 表示是否需要对第 $j$ 条分支进行调节； $n_{j, a}$ 满足 $n_{j, a} = \{\begin{matrix} 0, 当 |∆ h_{j}| \leq ρ_{j} \\ 1, 当 |∆ h_{j}| > ρ_{j} \end{matrix}$ ； $∆ h_{j}$ 为第 $j$ 条分支的风压调节值； $ρ_{j}$ 为第 $j$ 条分支允许忽略的调节量（调节因子），满足 $ρ_{j} > 0$ 。

3 通风网络优化调控数学模型

根据前文所述，基于多目标混合整数规划的风量调控分步优化模型可表示为

m i n Z = ω_{0} \sum_{j = 1}^{N} ∆ h_{j}^{'} + ω_{1} \sum_{j = 1}^{N} q_{j} (r_{j} q_{j}^{2} + ∆ h_{j} - h_{N j}) +

ω_{2} \sum_{j = 1}^{N} n_{j, a} |s_{j}| + ω_{3} (\sum_{j = 1, s_{j} > 0}^{N} n_{j, b} s_{j} - \sum_{j = 1, s_{j} < 0}^{N} n_{j, c} s_{j}) + ω_{4} \sum_{j = 1}^{N} n_{j, a}

s . t . \{\begin{matrix} \sum_{j = 1}^{N} b_{i j} h_{j} = 0 (i = 1,2, \dots, M) \\ - ρ_{j}^{'} \leq ∆ h_{j} \leq ρ_{j} ″ \\ ∆ h_{j, m i n} \leq ∆ h_{j} \leq ∆ h_{j, m a x} \\ \sum_{j = 1}^{N} n_{j, a} \leq N_{a} \\ ∆ h_{j}^{'} \geq ∆ h_{j} \\ ∆ h_{j}^{'} \geq - ∆ h_{j} \\ ∆ h_{j}^{'} - ρ_{j} \leq n_{m a x, a} n_{j, a} \\ ρ_{j} n_{j, a} \leq ∆ h_{j}^{'} \\ ∆ h_{j} - ρ_{j} \leq n_{m a x, b} n_{j, b} \\ - (∆ h_{j} + ρ_{j}) \leq n_{m a x, c} n_{j, c} \\ n_{j, b} + n_{j, c} = n_{j, a} \end{matrix}

（19）

数学模型中所有分支的风量均已知，决策变量为所有分支的调节风压值 $∆ h_{j}$ ，辅助决策变量为 $∆ h_{j}^{'}$ 、 $n_{j, a}$ 、 $n_{j, b}$ 和 $n_{j, c}$ 。由于已知风量可以看作常量，目标函数和约束条件均为线性函数，相应的数学模型为线性混合整数规划模型。

本文提出数学模型得到的结果为最优调节风压值，用于指导调控人员进行调控决策，需要结合通风网络解算软件，根据最优调节风压值确定最终的调控方案。其中，调节风压为负，表示该调节点位置需要进行增能调节或降阻调节；调节风压为正，表示该调节点位置需要进行增阻调节。此外，当某条分支为风机分支且该分支调节风压为负时，可以通过增加风机频率的方式进行增能调节；当某条分支为风机分支且该分支调节风压为正时，可以通过降低风机频率的方式进行降能调节。

由于调节模型是建立在通风网络解算的基础上，因此需要提前对通风网络进行按需分风解算，以便获得按需分风的风量分配结果。为了提高调控方案的灵活性，需要在满足按需分风要求的前提下，确定多组按需分风的风量分配结果。通过多次求解风量分配所对应的调控方案，该模型既可以得到近似满足风量未知调控模型的求解方案，也可以避免非线性模型求解不收敛的问题。

4 通风网络优化调控计算实例

基于作者所在团队早期研发的iVent三维矿井通风软件平台，采用C++编程语言进行二次开发实现了基于多目标混合整数规划的通风网络风流两步骤调控优化方法。通过该方法，用户可以任意新增和修改多目标参数和约束条件，以便获得一组满足实际调节需要的满意解。

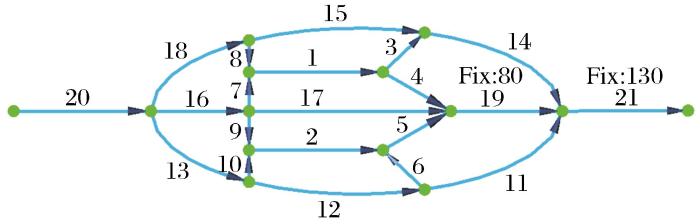
图1所示为一个简化的非煤矿山通风网络图，用于验证通风网络风量调控优化方法的可靠性，图中数字为通风网络分支编号。该通风网络共设置2个按需分风点，含有21条分支和14个节点。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 通风网络风量调控优化实例

Fig.1 Optimization example of ventilation network airflow regulation

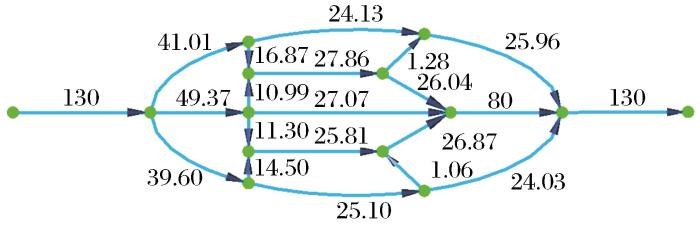
图2和表1为在按需分风前提下采用固定风量法得到的通风网络风量分配结果。在风量分配计算的基础上，采用风量调控多目标优化数学模型确定按需分风风量优化调控的方案。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 通风网络风量分配结果

Fig.2 Result of ventilation network airflow distribution

表1 通风网络风量分配结果

Table 1 Result of ventilation network airflow distribution

编号	位置	类型	长度/m	阻力系数 /（N·s²·m^-8）	风阻 /（N·s²·m^-8）	解算风量 /（m³·s^-1）	解算风压/Pa	风速 /（m·s^-1）	需风量 /（m³·s^-1）	调节风压/Pa
20	进风	一般	28.06	0.1000	0.0281	130.00	474.20	11.50	-	-
21	出风	定流	25.71	0.1000	0.0257	130.00	-568.52	11.50	130	-1 003.15
1	内部	一般	27.37	0.1100	0.0301	27.86	23.38	2.79	-	-
2	内部	一般	27.37	0.1300	0.0355	25.81	23.70	2.58	-	-
3	内部	一般	11.75	0.1000	0.0117	1.82	0.04	0.18	-	-
4	内部	一般	16.00	0.1100	0.0176	26.04	11.94	2.60	-	-
5	内部	一般	16.00	0.1000	0.0160	26.87	11.56	0.16	-	-
6	内部	一般	11.75	0.1100	0.0129	1.06	0.01	0.11	-	-
7	内部	一般	7.97	0.1000	0.0079	10.99	0.96	1.10	-	-
8	内部	一般	6.51	0.1000	0.0065	16.87	1.85	1.69	-	-
9	内部	一般	7.97	0.1000	0.0079	11.30	1.02	1.13	-	-
10	内部	一般	6.51	0.1000	0.0065	14.50	1.37	1.45	-	-
11	内部	一般	34.33	0.0800	0.0274	24.03	15.87	2.40	-	-
12	内部	一般	36.15	0.1100	0.0397	25.10	25.06	2.51	-	-
13	内部	一般	26.17	0.1300	0.0340	39.60	53.38	3.96	-	-
14	内部	一般	34.34	0.0700	0.0240	25.96	16.20	2.60	-	-
15	内部	一般	36.15	0.1200	0.0434	24.13	25.27	2.41	-	-
16	内部	一般	20.03	0.1100	0.0220	49.37	53.73	4.94	-	-
17	内部	一般	41.25	0.1200	0.0495	27.07	36.29	2.71	-	-
18	内部	一般	26.17	0.1200	0.0314	41.01	52.84	4.10	-	-
19	内部	定流	22.78	0.1300	0.0296	80.00	4.295	8.00	80	-185.28

新窗口打开| 下载CSV

表2为通风网络风量调节优化方案。其中，方案一为设置分支#19不可调得到的调节方案；方案二在设置了分支#19不可调的基础上，提高了调节点个数目标权重；方案三则在方案二的基础上，进一步提高了最少调节点个数目标权重；方案四在设置了分支#19不可调的基础上，提高了最佳调节方式目标权重。从调节方式来看，方案二和方案三的调节方案类似。由于没有设置调节级数，导致风量调控方案约束较弱。当设置分支#20的可调性低于分支#21时，优化求解得到的调节方案将更倾向于调节分支#21。

表2 通风网络风量调节优化方案

Table 2 Optimization schemes of ventilation network airflow regulation

调节方案	调节设置	编号	调节风压/Pa	调节方式
方案一	分支#19不可调	4	-185.28	增能
		17	-185.28	增能
		5	-185.28	增能
		21	-1 003.15	增能
方案二	分支#19不可调；提高调节点个数目标权重	11	185.28	增阻
		14	185.28	增阻
		20	-1 188.43	增能
方案三	分支#19不可调；提高最少调节点个数目标权重	11	185.28	增阻
		14	185.28	增阻
		21	-1 188.43	增能
方案四	分支#19不可调；提高最佳调节方式目标权重	11	185.28	增阻
		14	185.28	增阻
		21	-1 188.43	增能

新窗口打开| 下载CSV

根据风量调控多目标优化模型求解得到调节风压分配方案后，还应根据调节风压和井下实际情况确定最终的风量优化调控方案，最后利用风量分配方法模拟调节方案的实际调控效果。图3采用风机优选方法确定了按需分风分支#21增能调节备选风机列表，图4模拟了备选风机的运行工况。

图3

新窗口打开| 下载原图ZIP| 生成PPT

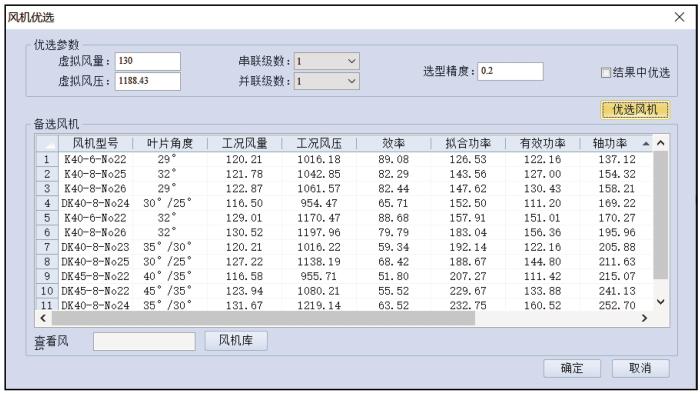
图3 按需分风分支#21增能调节备选风机列表

Fig.3 List of alternative fans based on energy-enhancing regulation of VOD branch #21

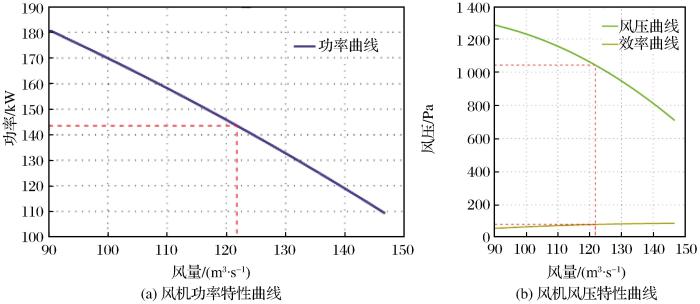
图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 备选风机K40-8-No25运行工况模拟

Fig.4 Running operation simulation for alternative fan K40-8-No25

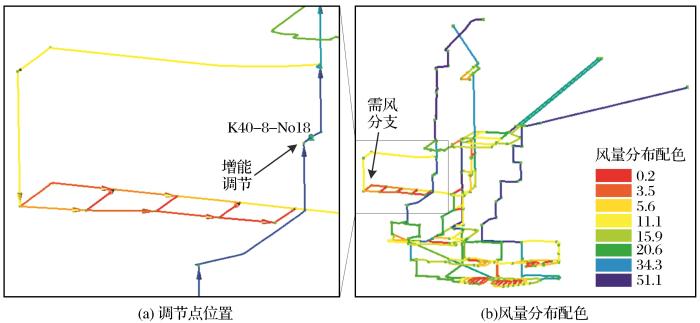
为了进一步测试通风网络优化调控数学模型的可靠性和算法执行效率，本文构建了一个较为复杂的非煤矿山通风网络模型并进行了调控计算。该通风网络模型如图5所示，含有272条分支和215个节点。由于数学模型为线性且决策变量个数较少，单次调控求解时间约为0.26 s。在两步骤计算时，需要准备多组风量分配方案分别进行调控计算，以确定较优的风量调控方案。如图5所示，设置需风分支（风量为7.70 m³/s，需风量为10.0 m³/s），经调控计算可在图5所示位置进行增能调节，调节后分支风量为10.25 m³/s。增能调节方案的风机型号为K40-8-No18，风机叶片安装角度为23°，风机工况风压为266.63 Pa，风机工况风量为40.49 m³/s。在结合通风网络解算软件的基础上，该两步骤调控法可以根据约束条件自动生成更多的风量分配方案，以避免遗漏更为可靠的风量调控方案。实际矿井通风系统较为复杂，未来仍然需要考虑更多因素来进一步完善数学模型。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 通风网络风量调控优化实例

Fig.5 Optimization example of ventilation network airflow regulation

5 结论

（1）为了提高通风网络优化调节方案的灵活性，通过引入混合整数规划方法，使该模型可以对调节方案的调节点个数和调节方式进行限制；通过引入分支调节级数使该模型可以根据井下实际情况对调节方案的位置进行限制。在矿井通风网络调节问题中，并非所有约束都需要严格满足，因此采用多目标规划的方法更有利于找到更加灵活可靠的调节方案。本文提出的通风网络风量调控优化多目标规划数学模型构造了最小通风能耗、最少调节点个数和最佳调节点位置等目标，使得模型求解结果更加符合矿山实际需要。

（2）通风网络风量分配优化基本数学模型是一个非凸、非线性规划模型，相应最优风量分配方案的求解十分困难，且模型求解的复杂度也随着决策变量数目（通风网络规模）的增加而急剧上升。本文在两步骤通风优化法的基础上，通过对多次给定风量分配方案进行线性求解的策略，将非线性数学模型进行线性化求解，可以避免非线性模型求解不收敛的问题。尽管单次两步骤调控计算得到的调控方案局限性较大，但采用多次给定风量分配方案进行线性求解的方法，可以得到类似非线性模型的调控方案，并且能够处理更为复杂的通风网络模型。

（3）发展风量未知的通风优化调控方法一直是矿井通风领域研究的重要方向，传统的优化策略一直集中于提高非线性模型求解的收敛性和收敛效率。然而，相比于线性调控数学模型，非线性调控数学模型求解仍然十分困难。实际上，除了多次给定风量分配方案进行线性求解的策略外，笔者正在研究通过变量离散化的策略将非线性数学模型转化为线性模型。矿井通风优化调控方法的未来发展方向在于尽可能提高优化调控线性大模型的求解效率。

中国矿业网

http://www.goldsci.ac.cn/article/2024/1005-2518/1005-2518-2024-32-2-356.shtml

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[]

Acuña

， Lowndes

I S

，2014.

A review of primary mine ventilation system optimization

［J］.Interfaces，44（2）：163-175.