基于PSO-XGBoost的露天矿山PPV预测模型研究

doi:10.11872/j.issn.1005-2518.2024.04.022

基于PSO-XGBoost的露天矿山PPV预测模型研究

李振阳^,¹, 张宝岗¹, 熊信², 杨承业², 白玉奇¹

1.北京奥信化工科技发展有限责任公司，北京 100040

2.中南大学资源与安全工程学院，湖南长沙 410083

Research on PPV Prediction Model of Open-pit Mine Based on PSO-XGBoost

LI Zhenyang^,¹, ZHANG Baogang¹, XIONG Xin², YANG Chengye², BAI Yuqi¹

1.Beijing Aoxin Chemical Technology Co. , Ltd. , Beijing 100040, China

2.School of Resources and Safety Engineering, Central South University, Changsha 410083, Hunan, China

收稿日期: 2024-01-11 修回日期: 2024-06-04

基金资助:

中南大学研究生自主探索创新项目“矿山多装备智能体协同调度优化及孪生仿真研究”. 1053320220742

Received: 2024-01-11 Revised: 2024-06-04

作者简介 About authors

李振阳（1993-），男，河北邯郸人，工程师，从事金属矿床开采及爆破工艺研究工作735424518@qq.com , E-mail：735424518@qq.com

摘要

爆破振动的质点峰值速度（Peak Particle Velocity，PPV）是评估爆破开采设计参数合理性的重要指标。为实现一种PPV有效预测模型，借助粒子群优化算法（Particle Swarm Optimization，PSO），结合优化极端梯度提升树（Extreme gradient boosting，XGBoost），构建了一种参数自优化的PSO-XGBoost预测模型。以LK露天铜钴矿为研究对象，选取最大单段炸药量、总炸药量、测量的爆心距、炮孔平均进深尺度和高程差共5个影响因素指标作为研究参数，通过现场收集187次爆破作业实测数据，进一步开展PPV的PSO-XGBoost预测研究，并与传统XGBoost模型、SSA-XGBoost优化模型及萨道夫斯基经验公式的PPV回归预测进行对比分析，最后利用Shapley Additive Explanatory（SHAP）方法开展影响PPV预测结果的敏感性因素分析。结果表明：PSO-XGBoost预测模型的预测评价指标计算结果最优（R²=0.921，RMSE=0.0752，MAE=0.0717，MBE=0.0683），其对PPV的预测结果明显优于传统XGBoost模型、SSA-XGBoost混合优化模型及萨道夫斯基经验公式，同时，敏感性分析得到总炸药用量是影响PPV预测结果的重要参数。进一步说明PSO-XGBoost预测模型可处理多因素的非线性特征，利用PSO-XGBoost预测模型能够更好地结合非线性、离散数据，建立一种可靠、简单有效的PPV预测模型。研究结果可为露天矿山爆破振动快速预测提供参考。

关键词： 露天矿山 ; 混合优化算法 ; 机器学习 ; 爆破振动 ; 回归分析

Abstract

The peak particle velocity（PPV） resulting from blasting vibration serves as a crucial metric in assessing the efficacy of blasting and mining design parameters.To enhance the accuracy of PPV predictions，a novel parameter self-optimizing PSO-XGBoost prediction model is introduced，leveraging the Particle Swarm Optimization （PSO） algorithm in conjunction with optimized Extreme Gradient Boosting （XGBoost）.The research focuses on the LK open-pit copper-cobalt mine and examines five influencing factors，namely the maximum single explosive charge，total explosive charge，measured distance to blast center，average depth of blastholes，and elevation difference，as study parameters.A total of 187 sets of measured data from on-site blasting operations are gathered for further investigation into predicting PPV using the PSO-XGBoost model.The findings indicate that the PSO-XGBoost prediction model produces superior prediction evaluation metrics （R²=0.921，RMSE=0.0752，MAE=0.0717，MBE=0.0683）， compared to alternative models，including the traditional XGBoost model，the SSA-XGBoost hybrid optimization model，and the Sariakaliski empirical formula.The sensitivity analysis reveals that the total explosive charge，significantly influences PPV prediction outcomes，underscoring the importance of using an appropriate amount of explosives to avoid energy inefficiency in blasting activities. Furthermore，the research demonstrates that the PSO-XGBoost prediction model，is capable of effectively addressing the nonlinear attributes of various factors，as well as integrating nonlinear and discrete data to develop a dependable，straightforward，and efficient PPV prediction model.This study offers valuable insights for promptly predicting blasting vibration in open-pit mining and assessing the impacts of blasting activities.

Keywords： open-pit mine ; hybrid optimizing algorithm ; machine learning ; blasting vibration ; regression analysis

PDF (5530KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李振阳, 张宝岗, 熊信, 杨承业, 白玉奇. 基于PSO-XGBoost的露天矿山PPV预测模型研究[J]. 黄金科学技术, 2024, 32(4): 620-630 doi:10.11872/j.issn.1005-2518.2024.04.022

LI Zhenyang, ZHANG Baogang, XIONG Xin, YANG Chengye, BAI Yuqi. Research on PPV Prediction Model of Open-pit Mine Based on PSO-XGBoost[J]. Gold Science and Technology, 2024, 32(4): 620-630 doi:10.11872/j.issn.1005-2518.2024.04.022

钻爆法是露天矿山开采的常用手段，炸药的爆破能量使矿岩发生破碎，实现矿石开采的目的（郭晓强，2021）。然而，不合理的爆破参数或炸药的使用，容易导致爆破能量的浪费，造成开采成本的增加，同时导致爆破震动和爆破飞石等安全问题，危害人员和设备的安全（史春宇等，2023）。因此，准确测量和评价现场爆破效果，有助于工程人员及时调整爆破参数，进一步优化钻爆法实际运用效果。其中，爆破振动的质点峰值速度（Peak Particle Velocity，PPV）是评价钻爆法所诱发振动的最常用指标（王子一等，2023），然而，由于爆破的突发性，部分参数难以进行准确测量。现有的PPV评价方法多基于现场测试的大量数据，通过人工经验公式进行回归拟合，但是人工经验公式通常仅考虑爆破距离和炸药用量等因素，同时，受限于炸药爆炸与岩土体介质的非线性、各向异性，以及岩土体性质随时间和温度变化、复杂边界条件等问题，拟合效果通常与实际值差距甚远（邓红卫等，2023）。

近年来，随着机器学习和人工智能等计算机技术的发展，利用算法对矿山工程中产生的非线性数据进行有效回归及拟合，有助于对PPV的数量少、非线性、多因素的样本数据进行有效的回归分析，从而指导矿山施工建设。这些方法包括但不限于BP神经网络、支持向量机和相关向量机等手段，实现了多因素耦合下的矿山开采PPV的预测（苟倩倩等，2018；胡晓冰等，2020；Trabi et al.，2023；Xuan et al.，2023；徐向东等，2023；曾晓辉等，2023）。何理等（2022）基于粒子群—最小二乘支持向量机模型，开展了矿山爆破振动速度预测，验证了该方法用于多因素影响下的矿山爆破 PPV 预测的可行性。Li et al.（2012）研究证实其所提出的振动速度 SVM预测模型具有可行性，且效果优于萨道夫斯基公式。邹平等（2023）利用SSA-XGBoost模型对矿山爆破 PPV进行了预测，结果表明SSA-XGBoost模型具有较高的预测精度和更好的稳定性。范勇等（2022）构建了基于PSO-BP 神经网络的PPV预测模型，并与萨道夫斯基公式进行对比分析，结果表明 PSO-BP 神经网络模型预测结果更为可靠。

上述研究表明，采用机器学习手段对PPV进行参数预测，可获得更精确的结果，较好地消除多因素、非线性特征对预测结果的影响。然而，以往研究仅开展PPV的预测研究，并未探究不同影响参数（如装药量和炮孔深度等）对PPV预测结果的影响。事实上，不同预测指标的变化对PPV的预测结果同样产生不同程度和不同方向的影响，分析这一变化可以帮助研究人员更加合理地选取预测指标，并根据预测结果进一步调整指标的选取及监测方式，获取更加合理准确的分析结果。同时，机器学习预测模型考虑的计算参数量多，对数据的噪点及异常值影响敏感、模型校验困难，不同计算参数对预测模型的精确程度影响很大，亟需探寻更加简便、合理且准确的PPV预测手段（Shirani et al.，2016；Khan-delwal et al.，2017）。

为此，本文引入一种分布式梯度增强库的XGBoost模型（Extreme Gradient Boosting，XGBoost）（张西良，2021），结合粒子群算法（PSO）对XGBoost算法进行自主优化，建立基于PSO-XGBoost的PPV预测模型，提出快速、精确的多因素指标露天矿山爆破振动预测方法。同时，引入Shapley Additive Explanatory（SHAP）模型，即一种机器学习可解释模型，开展多因素预测中露天矿山PPV的影响因素敏感性分析，揭示PPV的关键影响因素。

1 算法原理

1.1 XGBoost算法

极端梯度提升算法是一种优秀的决策树算法（Ma et al.，2023）。决策树是一种常见的机器学习方法，常用于分类和回归问题，由于其具有计算复杂度低、输出结果易于理解、对缺失的中间值不敏感以及能够处理不相关的特征数据等优点，被广泛应用于数据分析和数据挖掘等领域。然而，决策树方法存在稳定性差、对数据分布敏感、容易过拟合和泛化性能不可靠等缺点，限制了其应用的潜力（Hong et al.，2023）。随着人工智能技术的发展，研究人员提出了许多改进和优化决策树的方法，试图通过集成算法将普通弱评价器集成为强评价器，来消除决策树的这些缺点，提高决策树的性能。

XGBoost模型是将弱回归器或分类器组合成一个强预测模型来实现并行运行。由于其在处理分类和回归问题上的高性能，被广泛应用于数据挖掘和智能预测等领域（Tyagi et al.，2023）。在XGBoost模型中建立目标函数，并通过加入正则化项进行优化，巧妙地减少了过拟合问题，可为工程仿真提供快速可靠的模型。XGBoost模型根据以下公式进行数据预测：

O b j^{(r)} = \sum_{i = 1}^{m} L (y_{i}, {\hat{y}}^{(r)}) + \sum_{k = 1}^{r} Ω (g_{r})

（1）

式中：m为迭代次数； $y_{i}$ 为实测值； ${\hat{y}}^{(r)}$ 为第r次预测结果； $g_{r}$ 为决策树的项； $L (y_{i}, {\hat{y}}^{(r)})$ 为损失函数； $Ω (g_{r})$ 为正则化项。 $Ω (g_{r})$ 的计算公式为

Ω (g_{r}) = Υ T + \frac{1}{2} λ \sum_{j}^{T} ω^{2}

（2）

式中： $T$ 为决策树根节点； $ω$ 为各根节点的权重； $λ$ 和 $Υ$ 为系数，默认值为 $λ$ =1， $Υ$ =0。

1.2 PSO算法

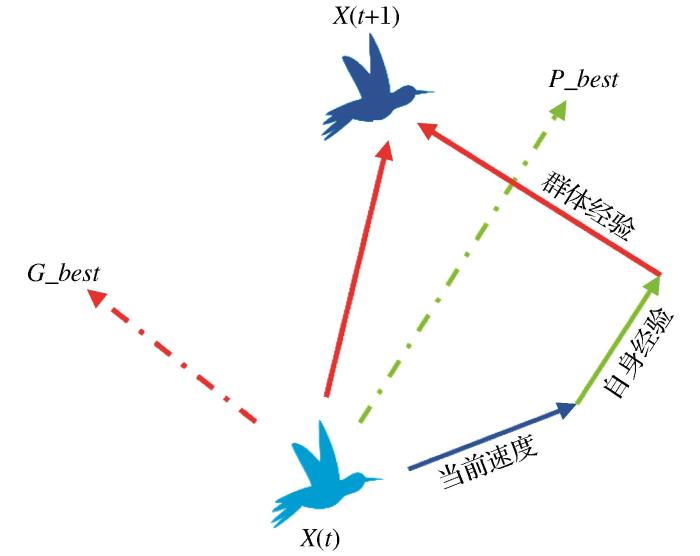
粒子群优化算法（Particle Swarm Optimization，PSO）是一种模拟鸟类觅食行为的启发式优化方法（董东林等，2023）。在PSO中，求解空间被视为一个多维环境，每个潜在解被表示为其中的一个粒子，而算法的优化目标则类比为鸟群寻找的食物源。

如图1所示，PSO的优化过程融合了个体经验和群体智慧。具体而言，每个粒子在搜索过程中会参考2个关键信息：自身历史最佳位置（ $P_b e s t$ ）和整个群体的全局最优解（ $G_b e s t$ ）。这2个参数分别代表了个体学习和群体学习的概念。PSO算法通过式（3）和式（4）不断调整其速度和位置，从而在求解空间中移动位置，不断获取最优解。为了评估各位置（各最优解）的优劣，算法引入了适应度函数这一关键概念。适应度函数直接对应于优化的目标，为粒子的移动提供了方向指引。这种机制确保了粒子能够在个体探索与群体合作之间取得平衡，从而高效地搜索解空间，逐步逼近最优解。

ν_{i j} (t + 1) = ν_{i j} (t) + c_{1} r_{1} [P_b e s t_{i j} (t) - x i_{j} (t)] +

c_{2} r_{2} [G_b e s t_{j} (t) - x_{i j} (t)]

（3）

x_{i j} (t + 1) = x_{i j} (t) + ν_{i j} (t + 1)

（4）

式中：j为粒子的维度；i为第i个粒子；t为当前迭代次数； $c_{1} 和 c_{2}$ 均为加速常量，通常在区间（0，2）内取值； $r_{1} 和 r_{2}$ 为2个取值范围在［0，1］的随机数。从式（3）和式（4）可以看出，c₁ 和c₂将粒子向个体学习和粒子向群体学习联合起来，使粒子能够同时借鉴个体自身和群体的搜索经验。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 PSO算法原理

Fig.1 Principle of PSO algorithm

1.3 PSO-XGBoost算法

基于XGBoost算法原理，在实现非线性回归预测的过程中，参数的正确选取对预测结果的可靠性具有决定性作用。影响XGBoost预测结果的主要参数有n_estimator、learning_rate、max_depth和gamma，见表1。通常在计算中通过人为调参获取拟合度更高的结果，但人为控制的主观影响无法避免，且容易陷入局部最优的结果。

表1 XGBoost模型计算参数

Table 1 Calculation parameters for XGBoost model

参数	参数说明
n_estimator	该参数决定了模型的预测能力，其值越大则模型的学习及数据分析能力越强，预测、结果越精确，但参数过大将浪费计算资源
learning_rate	该参数决定了迭代的步长，参数过大将影响运行的准确率，过小则影响运行的速度
max_depth	该参数表示为树的最大深度，用来控制算法的过拟合，其值越大则模型的学习将更具体
gamma	该参数指定了决策树节点分裂所需的最小损失函数下降值，其值越大，算法越保守

新窗口打开| 下载CSV

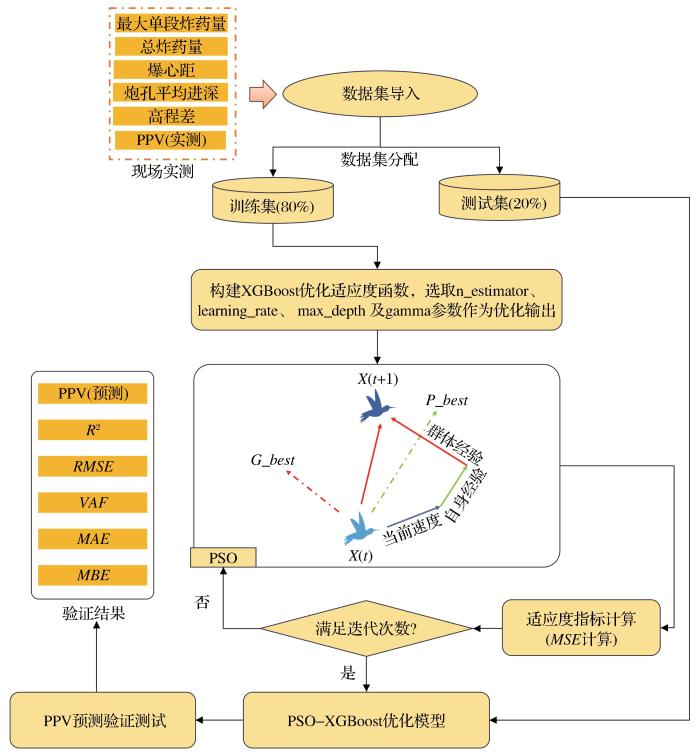
为获取更合理的预测结果，结合PSO算法的寻优原理，利用PSO算法对XGBoost的参数取值进行优化。PSO-XGBoost预测算法流程如图2所示，具体流程如下：

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 PSO-XGBoost预测算法流程

Fig.2 Process of PSO-XGBoost prediction algorithm

（1）输入数据集，构建PSO-XGBoost预测模型。

（2）设定初始PSO算法参数，构建PSO-XGBoost预测模型的适应度优化函数，将不同优化迭代次数下的预测模型均方误差（MSE）作为优化的适应度评价指标，表示为

M S E = \frac{\sum_{i = 1}^{N} (y_{i} - {\hat{y}}_{i})}{N}

（5）

式中： $y_{i}$ 为实际值； ${\hat{y}}_{i}$ 为预测值；N为预测的样本个数。MSE值越小，表示模型优化效果越好。

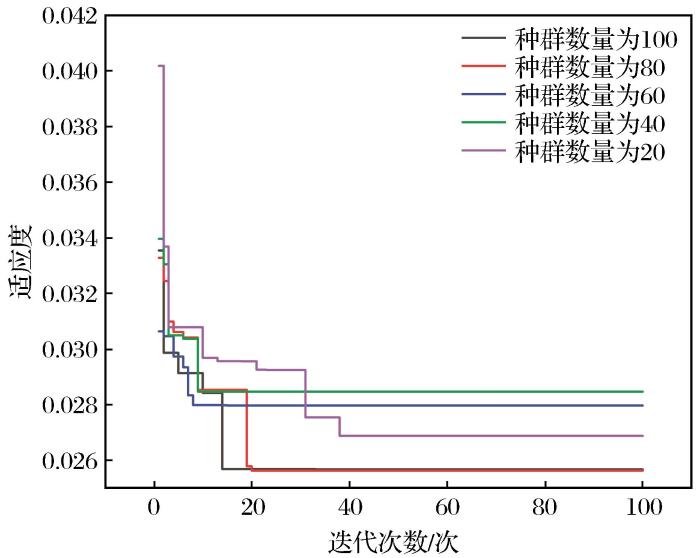
（3）针对XGBoost的最优参数选取，进行PSO算法迭代优化，并评估参数选取的适应度，调整PSO算法优化的种群数量，选取迭代过程中的适应度最小值作为最优值进行输出。

（4）输出XGBoost的最优参数，进行PPV预测及结果输出。

2 基于PSO-XGBoost的PPV预测模型构建

2.1 数据集构建

在露天开采过程中，PPV测量主要是利用爆破检测仪器，设置一定的测量距离，在已知炸药用量的情况下，获取爆破时刻的质点振动速度，再通过多次测量数据进行回归分析，得到炸药用量、爆心距离与爆破振动速度的经验关系，即萨道夫斯基经验公式（Sadovsky，1952）。萨道夫斯基经验公式表示为岩体某质点产生的振动速度ν与炸药量Q和距离R之间的关系：

ν = K {(\frac{\sqrt[3]{Q}}{R})}^{a}

（6）

式中：ν为振动速度（cm/s）；K为爆破振动波衰减系数；a为爆破振动波衰减指数。

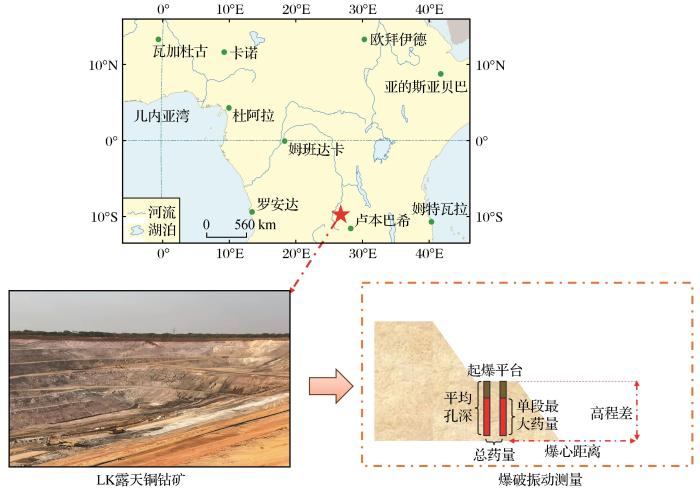
LK 露天铜钴矿位于刚果（金）科卢韦齐市，矿区水文地质条件复杂，采场内地下水极为丰富。随着开采深度的逐渐增加，采坑涌水量大幅增加，导致采坑排水压力较大。由于坑底排水设备较多且移动不便，在爆破过程中对飞石和爆破块度控制要求较高。因此，通过对采场的爆破振动进行预测，可减少繁琐的爆破振动测量过程，为采场爆破参数优化研究和爆破飞石控制提供重要的参数依据。通过对LK露天铜钴矿现场进行爆破振动数据实测（图3），选取实测的露天爆破过程中最大单段炸药量、总炸药量、测量的爆心距、炮孔平均进深尺度以及测量位置到爆破位置的高程差作为对应的影响参数，预测出PPV（Y），共收集到187次爆破作业数据，限于篇幅仅列出部分数据，见表2。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 研究区域与所选参数

Fig.3 Study area and selected parameters

表2 现场实测数据（部分）

Table 2 Field measured data（partial）

序号	最大单段炸药量/kg	总炸药量/kg	爆心距/m	孔深/m	高程差/m	PPV /（cm·s^-1）
1	22	256	41	10	5	4.1
2	15	231	56	12	3	2.3
3	18	245	48	11	6	3.4
4	19	243	49	11	3	3.7
5	17	235	62	13	6	2.9
6	15	240	54	12	4	3.1
︙	︙	︙	︙	︙	︙	︙
181	16	247	70	12	5	2.4
182	19	254	41	13	4	4.2
183	15	242	47	13	3	3.3
184	15	231	55	12	3	2.3
185	16	248	56	11	3	2.5
186	13	268	43	13	6	4.0
187	16	246	49	11	3	3.0

新窗口打开| 下载CSV

对所收集的数据进行相关性分析，结果如图4所示。由图4可以看出，测量的爆心距与PPV趋于线性关系，而其余数据间均表现为非线性关系。其中，最大单段炸药量、总炸药量、测量位置到爆破位置的高程差与PPV呈正相关关系，且以总炸药量与PPV的相关性最大，相关系数为0.587，认为总炸药用量越大，产生的PPV越大。此外，测量的爆心距、炮孔平均进深尺度与PPV的相关性均呈现负相关，其中测量的爆心距与PPV的相关性为-0.726，认为是监测位置与爆破中心距离越远，所监测到的PPV越小。

图4

新窗口打开| 下载原图ZIP| 生成PPT

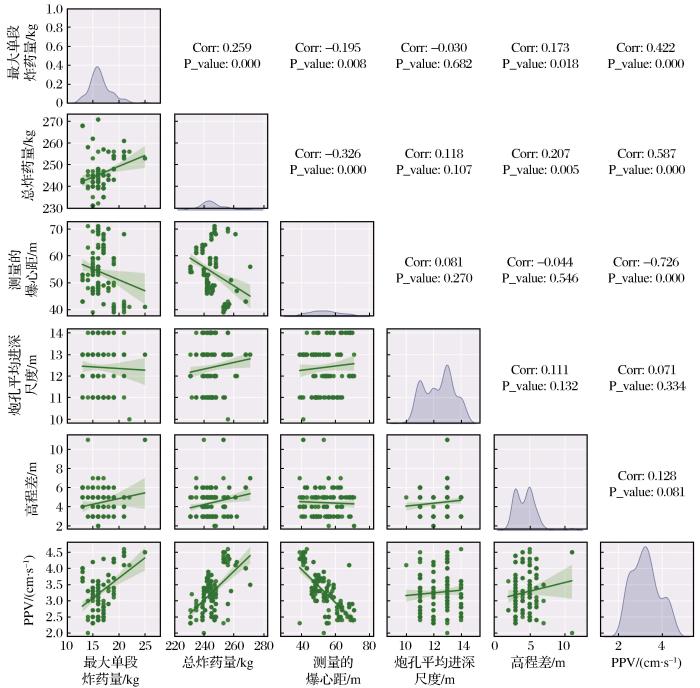
图4 数据集相关性矩阵分析

注：Corr和 P_value为2个参数之间的相关性。其中，Corr值越大表示2个参数之间的相关性越强，Corr的正负值表示正负相关性；P_value<0.05表示2个参数之间存在统计学意义上的相关性

Fig.4 Correlation matrix analysis of data set

2.2 预测评价指标

通过建立PSO-XGBoost回归预测模型，将所收集的80%数据作为训练集代入PSO-XGBoost模型中，进行预测模型训练，将20%数据作为预测对比数据的测试集，用于检验模型的预测准确性。进一步采用决定系数（R²）、预测模型均方误差（MSE）、平均绝对误差（MAE）和均方根误差（RMSE）等评价指标对所建立预测模型的可靠性和准确性进行评价和分析。这些评价指标用来描述PPV的预测值与实测值之间的关系，其计算公式（Zhou et al.，2021）分别表示为

R^{2} = 1 - \frac{\sum_{i = 1}^{N} (y_{i} - {\hat{y}}_{i})^{2}}{\sum_{i = 1}^{N} (y_{i} - {\bar{y}}_{i})^{2}}

（7）

M A E = \frac{\sum_{i = 1}^{N} {|y_{i} - {\hat{y}}_{i}|}^{2}}{N}

（8）

R M S E = \sqrt[]{\frac{\sum_{i = 1}^{N} {({\hat{y}}_{i -} y_{i})}^{2}}{N}}

（9）

式中： $y_{i}$ 为实际值； ${\overset{⌢}{y}}_{i}$ 为预测值； ${\bar{y}}_{i}$ 为实测平均值；N为预测的样本个数；R²的计算取值在0到1之间，通常R²>0.9说明模型预测的拟合效果较好；当MAE和RMSE的计算结果小于1时，说明模型预测值具有较好的可靠性，其值越小，说明预测值与实际值之间的误差值越小。

3 预测结果分析

3.1 预测模型参数优化结果

对于PSO算法，粒子种群数量决定了粒子寻优的准确性，不同粒子种群数量的优化结果各有差异，一般推荐选取的种群数为20~100。本文取种群数量分别为20、40、60、80、100，利用PSO算法对XGBoost进行参数选取优化预测，不同粒子种群数量的优化结果如图5所示。由图5可以看出，在不同种群数量的PSO算法优化下，适应度在迭代次数为60次之后均达到收敛，当种群数量为80时，优化结果的适应度值最低（0.0256），选取最低适应度的参数作为预测PPV的最优参数，如表3所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 优化适应度收敛

Fig.5 Optimization fitness convergence

表3 最优计算参数

Table 3 Optimal calculation parameters

参数	参数取值
n_estimator	6.56e+02
learning_rate	3.04e-02
max_depth	3.49
gamma	6.95e-03

新窗口打开| 下载CSV

3.2 预测结果分析

为进一步验证PSO-XGBoost模型预测PPV的准确性，选取传统XGBoost模型和萨道夫斯基经验公式进行数据的回归预测，对比分析了PSO-XGBoost模型与传统XGBoost算法模型、基于SSA优化的XGBoost算法模型及萨道夫斯基经验公式的回归结果，如图6所示。其中，PSO-XGBoost预测模型选取现场实测参数（表2）进行预测，XGBoost算法模型则采用初始默认参数进行预测。

图6

新窗口打开| 下载原图ZIP| 生成PPT

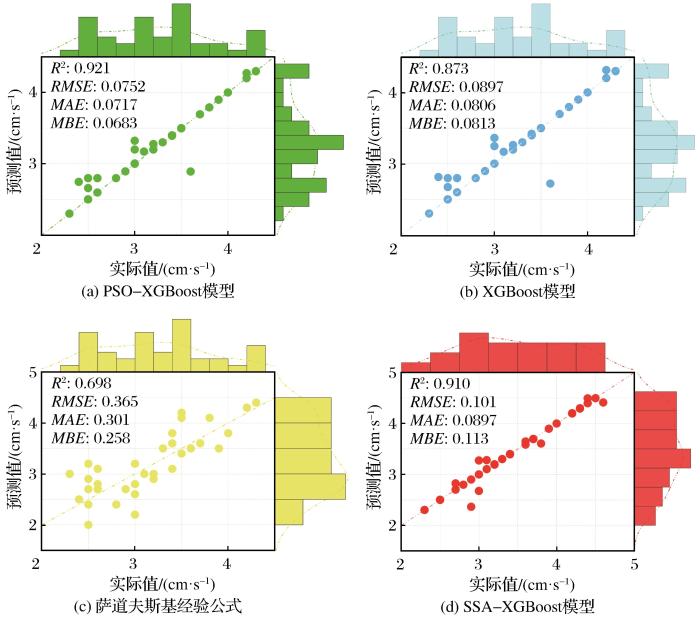
图6 不同模型回归预测结果比较

Fig.6 Comparison of regression prediction results of different models

由图6可知，数据点越接近真实值线，表明预测值与实测值相差越小。从3种模型的预测结果来看，采用PSO-XGBoost预测模型对PPV进行预测的结果最优，其中预测值与真实值的决定系数R²可达到0.921，说明该模型的预测值与实际值接近；进一步对比预测值与实际值之间的误差，可以看出PSO-XGBoost预测模型的MSE、MAE 和RMSE的值均为最低值，说明PSO-XGBoost预测模型对PPV的非线性拟合效果较好，数据的离散程度得到了有效控制。

与传统XGBoost预测模型相比，PSO-XGBoost预测模型的准确度明显更优，说明PSO算法对于XGBoost模型的参数选取具有较好的优化作用，可得到预测拟合的较优值。与萨道夫斯基经验公式的回归预测结果相比，采用机器学习模型后，模型预测的准确率得到大幅提高，说明机器学习模型更适用于PPV这类非线性拟合数据的预测。同时，与其他种群优化算法（麻雀算法，SSA）进行对比，结果表明2种优化算法均提高了XGBoost模型对PPV预测的准确度，但PSO算法的优化效果更好，证实了PSO-XGBoost算法用于PPV预测更具优势。

3.3 敏感性分析

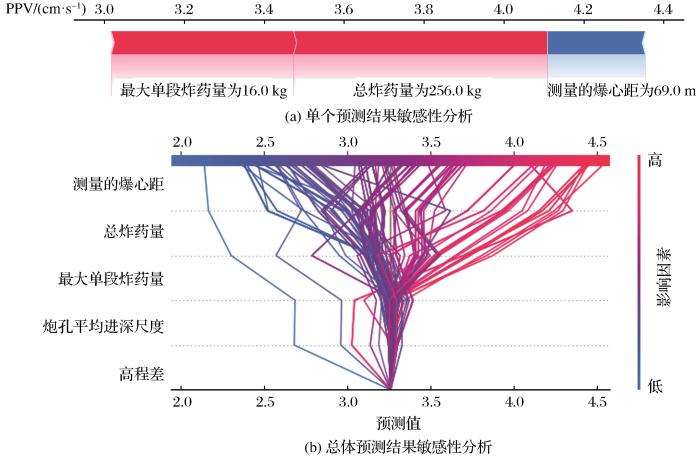
前文分析表明，采用多因素指标对PPV进行预测可以提高预测结果的准确率。为此，进一步开展不同因素（最大单段炸药量、总炸药量、测量的爆心距、炮孔平均进深尺度、测量位置到爆破位置的高程）变化对PPV预测结果的敏感性分析，用于判断不同因素指标对预测结果的贡献。为了探索和比较不同影响因素对PPV的敏感性，采用Shapley Addi-tive explanatory （SHAP）（Yu et al.，2023）方法揭示特征的重要性及其对PPV预测的贡献。SHAP是一种事后模型解释方法，通过计算特征加入模型时的边际贡献，并考虑该特征在所有特征序列中的不同边际贡献，从全局和局部2个层面对模型进行解释。对于每个预测样本，SHAP模型生成一个预测值来衡量特征对模型的重要性。基本数学公式如下：

Φ_{i} = \sum_{S \subseteq N (i)} \frac{|S|! (|N| - |S| - 1)!}{|N|!} \sqrt[]{\frac{\sum_{i = 1}^{N} {({\hat{y}}_{i -} y_{i})}^{2}}{N}} [q_{S ⋃ i} (x_{S ⋃ i}) - q_{S} (x_{S})]

（10）

式中： $Φ_{i}$ 为第i个特征的重要性；N为数据集的所有特征；S为N去除索引i后的子集； $x_{S}$ 为集合S中的输入特征；q为特征的贡献函数。

不同特征对PPV预测结果的影响程度大小如图7（a）所示，其中红色代表因素指标对预测结果为正贡献，蓝色代表因素指标对预测结果为负贡献，颜色区域宽度越大，说明该特征的影响越大。由图7（a）可以看出，最大单段炸药量与总炸药量的正贡献值较大，说明过大的装药量会造成PPV数值偏大，容易造成爆破能量的浪费。测量的爆心距对PPV预测结果造成的负贡献值最大，测量的爆心距变大会造成PPV预测结果减小。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 SHAP敏感性分析

Fig.7 Sensitivity analysis of SHAP

进一步统计分析每个样本的输入特征对模型输出的影响分布，结果如图7（b）所示。由图7（b）可以看出，测量的爆心距的全局重要性最大（影响程度在图中按从大至小、由上至下排列），总炸药量次之。随着测量的爆心距的增大，PPV预测结果减小，随着总炸药量的增加，PPV预测结果增大。研究认为，测量的爆心距是由于人为测量而影响PPV的主观因素，而总炸药量是真正影响PPV的直接因素。因此，在对爆破参数进行分析时发现，过大的装药量或不合理的装药结构均会造成PPV预测结果过大，导致爆破能量的浪费。

此外，炮孔平均进深尺度与PPV呈现正相关趋势，而高程差与PPV呈现负相关趋势，即测量点炮孔的进深越大，装药量相对增大，测量得到的PPV更大，而测量点与爆破区域的高程差越大，PPV测量值越小。

4 结论

（1）选取最大单段炸药量、总炸药量、测量的爆心距、炮孔平均进深尺度以及测量位置到爆破位置的高程差作为对应的影响参数，进行PPV预测的影响因素分析。通过相关性矩阵得到，爆心距与PPV呈近似线性关系，而其余数据间均表现为非线性相关。其中，总炸药量与PPV的相关性最大，为0.587，认为在其余因素不变的前提下，总炸药用量越大，产生的PPV越大。

（2）通过选取PSO不同种群数量进行迭代优化，得出当种群数量为80时，获取的参数适应度最佳，并将最优参数代入PSO-XGBoost预测模型中，分别与XGBoost预测模型、萨道夫斯基经验公式以及SSA-XGBoost等其他种群优化算法进行PPV的预测回归对比，分析得到PSO-XGBoost预测模型的预测指标最优，其中R²=921，MSE=0.0717，MAE=0.0683，RMSE=0.0752，认为PPV预测结果及误差控制均优于XGBoost预测模型、萨道夫斯基经验公式和SSA-XGBoost模型。

（3）结合先进的SHAP值方法对组合模型进行分析，揭示了5个因素指标对PPV预测的贡献，提高了预测的解释能力。从SHAP结果可以看出，测量的爆心距对PPV预测结果的影响最大，但总炸药量才是真正影响PPV的直接因素。因此，在对爆破参数进行优化时，应选取合理的装药量和装药结构，减少爆破振动对周边建筑物及人员、设备的影响。

中关村绿色矿山产业联盟）

http://www.goldsci.ac.cn/article/2024/1005-2518/1005-2518-2024-32-4-620.shtml

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[]

Deng

Hongwei

， Luo

Liang

，2023.

PPV prediction model based on random forest optimized by SMA algorithm

［J］.Gold Science and Technology，31（4）：624-634.

Dong

Donglin

， Zhang

Longqiang

， Zhang

Enyu

，et al，2023.

A rapid identification model of mine water inrush based on PSO-XGBoost

［J］.Coal Science and Technology，51（7）：72-82.

Fan

Yong

， Pei

Yong

， Yang

Guangdong

，et al，2022.

Prediction of blasting vibration velocity peak based on an improved PSO-BP neural network

［J］.Journal of Vibration and Shock，41（16）：194-200.

Gou

Qianqian

， Zhao

Mingsheng

， Chi

En’an

，et al，2018.

Prediction and application of evaluation factors in blasting vibration based on PCA-BP neural network

［J］.Mining Research and Development，38（12）：97-102.

Guo

Xiaoqiang

，2021.

Study on the determination of the limit distance of boundary borehole based on blasting vibration

［J］.Mining Research and Development，41（6）：26-30.

， Liu

Yihe

， Li

Linna

，et al，2022.

Prediction of mine Blasting vibration velocity of mines based on particle swarm -least square support vector machine model

［J］.Metal Mines，51（7）：145-150.

Hong

Z X

， Tao

， Liu

L L

，et al，2023.

An intelligent approach for predicting overbreak in underground blasting operation based on an optimized XGBoost model

［J］.Engineering Applications of Artificial Intelligence，126（2）：1-16.

序号	最大单段炸药量/kg	总炸药量/kg	爆心距/m	孔深/m	高程差/m	PPV /（cm·s^-1）
1	22	256	41	10	5	4.1
2	15	231	56	12	3	2.3
3	18	245	48	11	6	3.4
4	19	243	49	11	3	3.7
5	17	235	62	13	6	2.9
6	15	240	54	12	4	3.1
︙	︙	︙	︙	︙	︙	︙
181	16	247	70	12	5	2.4
182	19	254	41	13	4	4.2
183	15	242	47	13	3	3.3
184	15	231	55	12	3	2.3
185	16	248	56	11	3	2.5
186	13	268	43	13	6	4.0
187	16	246	49	11	3	3.0

序号	最大单段炸药量/kg	总炸药量/kg	爆心距/m	孔深/m	高程差/m	PPV /（cm·s^-1）
1	22	256	41	10	5	4.1
2	15	231	56	12	3	2.3
3	18	245	48	11	6	3.4
4	19	243	49	11	3	3.7
5	17	235	62	13	6	2.9
6	15	240	54	12	4	3.1
︙	︙	︙	︙	︙	︙	︙
181	16	247	70	12	5	2.4
182	19	254	41	13	4	4.2
183	15	242	47	13	3	3.3
184	15	231	55	12	3	2.3
185	16	248	56	11	3	2.5
186	13	268	43	13	6	4.0
187	16	246	49	11	3	3.0