矿产资源是国家经济建设的重要支柱,被广泛应用于工业生产、建筑和能源等领域(Zhang et al.,2012;Cui et al.,2014;Deng et al.,2020)。然而,采矿活动所带来的各种地质破坏问题给资源开发和环境保护带来了巨大挑战。地表塌陷是其中最突出的问题之一,其发生机理主要与岩层移动有关(钱鸣高等,1982;赵国景等,1987;秦朝亮等,2015)。在矿石开采过程中,地下岩层的移动会导致地表出现裂缝和沉降,最终形成地表塌陷的危险。
在进行“三下”压覆矿产资源开采时,不仅要解决回采技术的问题,而且要严格控制覆岩沉降。目前,国内外学者对岩层移动控制的研究主要集中在2个方面:一是关于顶板和覆岩移动力学机理的研究;二是关于地表沉降和非连续变形方面的研究。关于顶板和覆岩移动力学机理的研究,Ortlepp et al.(1998)发现通过更强的支撑来抑制所涉及的能量是不现实的,相反,支架必须屈服,并在屈服时吸收能量,在具有合适变形能力的让压支护条件下,能够吸收非常剧烈的静态和动态变形。马少维(2022)建立了基于虚拟拱理论的顶板—充填体耦合模型,提出了一种深部矿体多单元组合系统开采技术。关于地表沉降和非连续变形方面的研究,Loganathan et al.(1998)早在20世纪90年代就提出将地层损失参数重新定义为等效圆形损失参数,并将其纳入到对黏土地层元素的分析预测中。聂宇旭(2023)通过拟合相似模型试验的采动裂隙图像数据,分析得出裂隙率、裂隙总长度与裂隙网络分形维数近似呈对数关系。研究表明,岩层与地表沉陷行为主要受充填材料、地应力和工作面尺寸等因素的综合影响(朱时东,2015;兰立信,2018;郭凯凯,2022),而计算不同影响因素下岩层及地表移动的方法主要有弹性地基梁理论、概率积分法和GIS技术等(戴华阳,2002;Kim et al.,2006;徐阳,2023)。其中,概率积分法将岩层移动看作服从统计规律的随机过程,具有广泛适用性,目前多应用于煤矿充填开采的岩层移动计算(王正帅,2011)。与概率积分法相比,影响函数法计算过程简便,通过建立覆岩移动模型能够更快速准确地预测地表沉陷(Wang et al.,2020)。
然而,目前关于岩层移动规律与控制的研究成果局限于对煤矿地表移动变形进行预测,而鲜有关于金属矿方面的研究,关于金属矿上覆岩层变形机理尚不明确。尽管各大矿山采取充填的方式控制沉降,但仍有地表裂隙的产生。因此,本文根据盘龙铅锌矿开采条件,开展金属矿山覆岩移动沉降规律研究,根据沉降机理采取相对应的有效控制措施,并将其应用于工业试验,以期为金属矿山开采方案设计提供依据。
1 工程背景
盘龙铅锌矿位于来宾市,矿区为残丘平原地貌。该矿区地表开采环境极其复杂,地表有大藤峡水利枢纽工程(东西帷幕注浆)、桂平至来宾高速公路和回风竖井等工程,造成井下压覆铅锌矿矿石资源储量超过800万t。矿区共圈定铅锌硫化矿体16个,赋存于下泥盆统上伦组上部白云岩层间破碎带中,属于隐伏矿体,最高赋存标高为62 m,由多层平行排列的矿脉组成,形态主要为层状、似层状和透镜状,局部呈囊状,一般中间厚、边部薄,呈楔形分枝或尖灭,且具有尖灭再现和分枝复合现象。矿体沿NE⁃SW向延展,产状与围岩基本一致,总体倾向340°,倾角为77°~88°,平均倾角为82°,在剖面上呈陡立的板柱状延伸,局部地段直立或反倾。
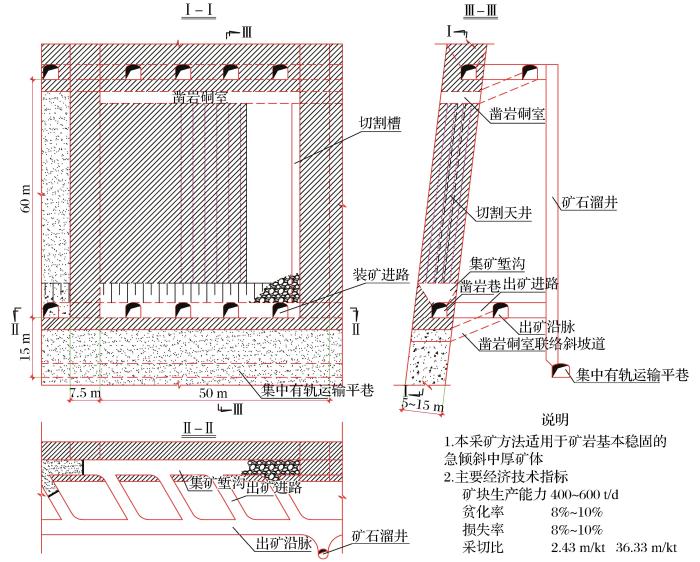
盘龙铅锌矿采用大直径深孔侧向崩矿嗣后充填采矿法,如图1所示。沿走向按70~105 m划分为一个盘区,盘区宽度为矿体水平厚度,盘区垂高为60 m,即中段高度,盘区间不留盘区间柱。盘区内划分5~7个矿块,矿块沿走向布置,分矿房、矿柱两步骤回采。矿块长度为50~60 m,宽度为矿体水平厚度,垂高为60 m,即中段高度,矿块留间柱和底柱,间柱宽6~8 m,底柱高13 m。矿房和矿柱回采结束后采用分级尾砂胶结充填采空区。
图1
图1
大直径深孔侧向崩矿嗣后充填采矿方法示意图
Fig.1
Schematic diagram of backfill mining method following large-diameter deep-hole sideways ore caving
2 基于非线性弹性地基梁的覆岩移动力学机理
2.1 充填开采非线性弹性地基梁模型
地下矿体开挖后形成采空区,随着采空区滞留时间延长,上覆岩层逐渐下沉变形,与此同时岩体内裂隙逐渐扩张。当覆岩下沉到一定程度,岩体内节理裂隙大量导通发展成断层,随后引起顶板冒顶和地表塌陷等一系列生产事故。若是将采空区全部充填,由采空区支撑顶板阻止其发生变形,限制其移动空间,将会起到很好的保护岩层稳定的作用。在未开采的区域,矿层未受到破坏,在其具有弹性的范围内可被视为Winkler弹性地基(Zhang et al.,2018);对于采空区内的充填体,在受到覆岩的挤压作用下,随着充填体逐渐被压实,其对覆岩的支撑力也逐渐增强。这种增强过程使得弹性地基系数呈非线性变化,因此,采场对应的范围被视为具有非线性弹性地基的区域(黄丹等,2024)。
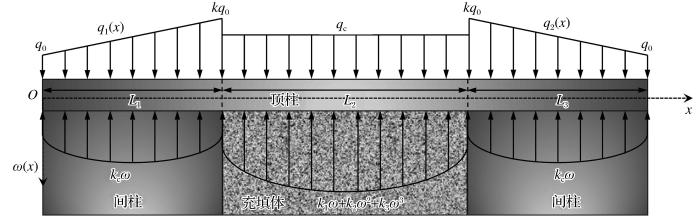
图2所示为盘龙铅锌矿采场充填开采的简化模型。图中,q0为原岩应力;k为应力集中系数;qc为顶板所受载荷;L1和L3分别为两端支撑压力区长度(一般默认相等);L2为工作面推进长度,挠度为ω(x);k1、k2和k3为充填体的非线性弹性地基系数。
图2
图2
非线性弹性地基顶板受力分析模型
Fig.2
Analysis model of stress on nonlinear elastic foundation roof
(1)当0≤x≤L1时,左侧边界矿体未被采动,视为线弹性地基,地基反力
式中:kc为矿体的弹性地基系数(N/m3)。
左端非线性载荷可由下式计算:
得到直接顶板的挠度微分方程为
式中:E为弹性模量(GPa),盘龙铅锌矿矿体弹性模量取30 GPa;I为梁截面惯性矩(m4),根据弹性力学有
(2)当L1≤x≤L1+L2时,地基反力
式中:k1、k2和k3为充填体的非线性弹性地基系数(N/m3)。
得到直接顶板的挠度微分方程为
式中:qc=γ∙Hq,Hq为顶板上覆岩层预计冒落高度(m);γ为岩石的容重(N/m3)。
(3)当L1+L2≤x≤L1+L2+L3时,根据图2地基模型的对称性,地基反力
地基顶板上方荷载表示为
得到直接顶板的挠度微分方程为
根据挠度与内力的换算关系,可由下式分别求得转角θ(x)、弯矩M(x)和剪力Q(x),即:
该力学模型存在以下边界条件:
2.2 岩层参数与覆岩移动影响因素分析
针对上述方程组,根据盘龙铅锌矿现场条件取值如下:E=30 GPa;L1和L3取L2的16%左右,工作面推进长度L2依具体情况而定;应力集中系数k根据现场应力测试结果取1.99;充填体上方直接顶所受均布荷载qc根据矿岩容重3 430 kg/m3计算得到,为1.65 MPa;矿体弹性地基系数kc根据现场采样作力学测试最终取1.45×109 N/m3。取现场1∶8配比充填体开展力学测试,得到地基系数分别为k1=4.57×106 N/m3,k2=8.07×106 N/m3,k3=9.25×106 N/m3,直接顶厚度取hz=8 m。
根据建立的三段非线性弹性地基微分方程,自变量为工作面推进方向长度,求解该微分方程组的定解时,需满足边界条件,即微分方程的特定解。本文将对上式使用MATLAB编码解算,求解顶板挠度和内力。本节将按照不同采场宽度、采场长度、顶板厚度、原岩应力和充填配比5种情况分别进行比较讨论,分析其差异性。
(1)采场宽度对覆岩移动的影响规律
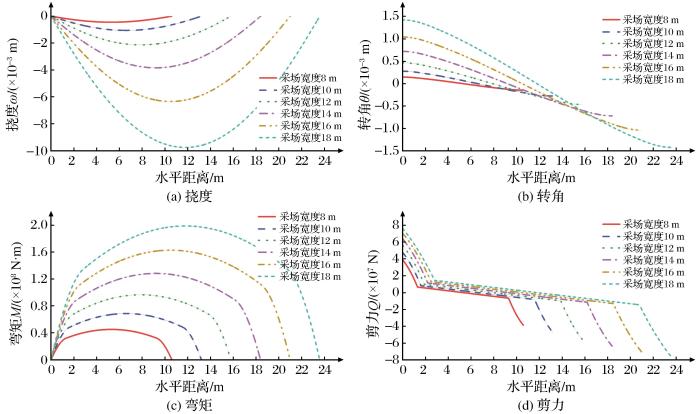
将岩层相关参数代入非线性弹性地基梁三段方程组,采场宽度L2分别为8,10,12,14,16,18 m时,MATLAB数值计算及处理地基顶板挠度与内力的结果如图3所示。
图3
图3
不同采场宽度条件下非线性弹性地基顶板挠度与内力结果对比
Fig.3
Comparison of deflection and internal force results of nonlinear elastic foundation roof under the condition of different mining field widths
由图3可知,顶板的挠度与内力围绕其中点呈对称分布,且峰值随着采场宽度的增加而逐渐增大。当采场宽度为8 m时,挠度、转角、弯矩和剪力分别为-0.45 mm、0.15 mm、0.45×108 N·m和3.87×107 N;当采场宽度为18 m时,其值分别为-9.77 mm、1.43 mm、1.99×108 N·m和7.62×107 N,变化值分别是采场宽度为8 m时的20.71倍、8.53倍、3.42倍和0.97倍。据此可知,挠度受采场宽度的影响最大,其次为转角、弯矩和剪力。
(2)采场长度对覆岩移动的影响规律
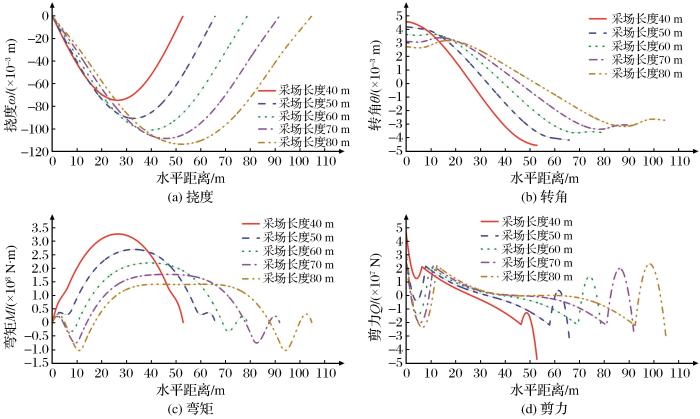
将岩层相关参数代入非线性弹性地基梁三段方程组,采场长度分别取40,50,60,70,80 m,代入方程组计算得到顶板挠度与内力的结果如图4所示。
图4
图4
不同采场长度条件下非线性弹性地基顶板挠度与内力结果对比
Fig.4
Comparison of deflection and internal force results of nonlinear elastic foundation roof under the condition of different mining field lengths
由图4可知,转角和剪力随着采场长度的增加变化不明显,挠度随着采场长度的增加而逐渐变大,5种采场长度的挠度最大值分别为-74.7,-90.7,-101.1,-108.5,-113.6 mm,增长率分别为21.48%、11.45%、7.31%和4.69%,说明随着采场长度的增加,顶板挠度逐渐趋于一个稳定值。而弯矩却随着采场长度的增加呈现逐渐减小的趋势,弯矩减小后,直接顶板中最大抗拉强度降低,从而减小了覆岩移动范围。
(3)顶板厚度对覆岩移动的影响规律
将岩层相关参数代入非线性弹性地基梁三段方程组,顶板厚度分别取7,8,9,10,11,12 m,工作面长度L2取14 m(下文皆取此值),计算得到顶板挠度与内力的结果如图5所示。
图5
图5
不同顶板厚度条件下非线性弹性地基顶板挠度与内力结果对比
Fig.5
Comparison of deflection and internal force results of nonlinear elastic foundation roof under the condition of different roof thicknesses
由图5可知,随着顶板厚度的增加,挠度逐渐减小,最大挠度依次为-19.7,-13.4,-9.5,-6.98,-5.3 mm,而转角、弯矩和剪力的变化很小,说明顶板厚度对于挠度的影响较大,而对内力的影响较小。剪力曲线和转角曲线关于空区中心位置呈反对称分布,且在区域2.2 m≤x≤16.2 m内,5种剪力曲线大小相差极小。
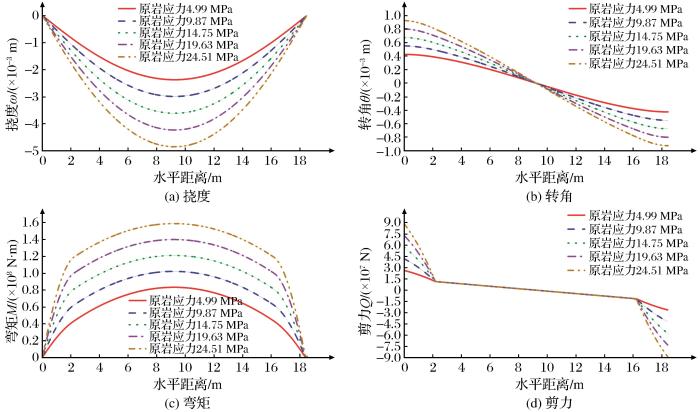
(4)原岩应力对覆岩移动的影响规律
根据盘龙铅锌矿现场原岩应力测试(虎万杰,2023),得到应力随深度变化的规律如
式中:H为矿体埋深(m);σ1为最大主应力;σ2为中间主应力;σ3为最小主应力。
该部分将选取200,400,600,800,1 000 m共5种埋深研究不同原岩应力对充填开采覆岩移动的影响规律,根据
图6
图6
不同原岩应力条件下非线性弹性地基顶板挠度与内力结果对比
Fig.6
Comparison of deflection and internal force results of nonlinear elastic foundation roof under the condition of different original rock stresses
挠度、转角、弯矩和剪力随着原岩应力的均匀增加而均匀增加,说明挠度和内力与原岩应力呈正相关关系。随着原岩应力的增加,最大挠度平均变化-0.62×10-3 m,最大转角平均变化0.12×10-3 m,最大弯矩平均变化0.19×108 N·m,最大剪力平均变化1.56×107 N。这说明地基顶板发生沉降与岩梁自身荷载及其上可能存在的冒落体有关,而与整体埋深关系较小。顶板剪力值在地基梁位置基本重合,主要是由于地基岩梁所受荷载与原岩应力无关;原岩应力直接作用于侧限边界,因此侧限边界的剪力随原岩应力的增大呈线性增大。
(5)充填配比对覆岩移动的影响规律
充填体的弹性地基系数k与充填体的弹性模量E0和厚度t0有关(罗霄,2021),关系式为
本文充填配比取值依据国内各大矿山充填工艺,分别取1∶4、1∶8、1∶10和1∶12作为该部分计算参数。将不同配比充填体的弹性模量代入
表1 4种充填体配比下的弹性地基系数
Table 1
| 序号 | 充填配比 | k1/(N∙m-3) | k2/(N∙m-3) | k3/(N∙m-3) |
|---|---|---|---|---|
| 1 | 1∶4 | 1.13×107 | 2.00×107 | 2.29×107 |
| 2 | 1∶8 | 4.57×106 | 8.07×106 | 9.25×106 |
| 3 | 1∶10 | 2.79×106 | 4.93×106 | 5.65×106 |
| 4 | 1∶12 | 1.92×106 | 3.39×106 | 3.88×106 |
图7
图7
不同充填配比条件下非线性弹性地基顶板挠度与内力结果对比
Fig.7
Comparison of deflection and internal force results of nonlinear elastic foundation roof under the condition of different backfill ratio
3 覆岩移动规律的数值模拟验证
上文通过构建力学模型研究了5种不同影响因素下的充填采空区顶板移动规律,本节将采用FLAC3D构建数值分析模型,计算充填配比为1∶4、1∶8、1∶10和1∶12时上覆岩层的位移,验证非线性弹性地基梁力学模型计算结果的可靠性。
3.1 数值模型构建
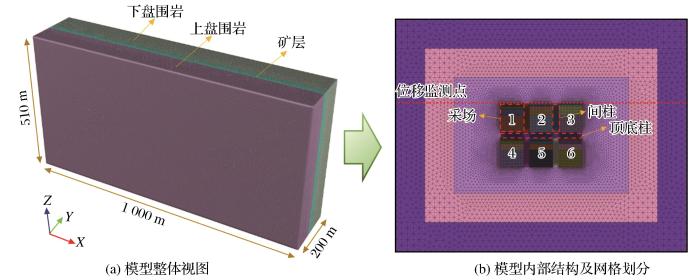
根据圣维南原理,为了消除边界效应,模型尺寸应为开挖区域的3~5倍,因此数值模型整体尺寸取长×宽×高=1 000 m×200 m×510 m,总共划分1 786 690个单元体。其中,阶段高度均为60 m,间柱宽10 m,顶底柱厚10 m,采场长度为40 m,采场宽度为16 m,采场顶板等间距设置101个位移监测点,如图8所示。将盘龙铅锌矿岩体及充填体物理力学参数采用推广的Hoek-Brown强度折减准则进行折减(韩龙强等,2016),最终得到数值模拟计算参数如表2所示。模型采用位移边界条件,即四周采用滚支撑,底面固定,顶部为自由面。只考虑自重应力的作用,不考虑断层、节理裂隙及岩石交界面的影响。
图8
表2 矿岩及充填体物理力学参数
Table 2
| 岩性 | 容重/(kg·m-3) | 弹性模量/GPa | 泊松比 | 内摩擦角/(°) | 黏聚力/MPa | 抗拉强度/MPa | 体积模量/GPa | 剪切模量/GPa |
|---|---|---|---|---|---|---|---|---|
| 矿体 | 3 430 | 30 | 0.24 | 32 | 4.24 | 3.5 | 19.2 | 12.1 |
| 上盘围岩 | 2 680 | 32 | 0.23 | 34 | 5.12 | 3.7 | 19.8 | 13.0 |
| 下盘围岩 | 2 700 | 35 | 0.23 | 33 | 4.80 | 4.5 | 21.6 | 14.2 |
| 充填体(1∶4) | 1 980 | 0.0573 | 0.184 | 41.5 | 0.282 | 0.45 | 0.0302 | 0.0242 |
| 充填体(1∶8) | 1 890 | 0.0231 | 0.196 | 38.7 | 0.171 | 0.17 | 0.0127 | 0.0097 |
| 充填体(1∶10) | 1 830 | 0.0141 | 0.215 | 36.9 | 0.143 | 0.1 | 0.0082 | 0.0058 |
| 充填体(1∶12) | 1 720 | 0.0097 | 0.227 | 33.2 | 0.105 | 0.02 | 0.0059 | 0.0040 |
3.2 数值模拟结果分析
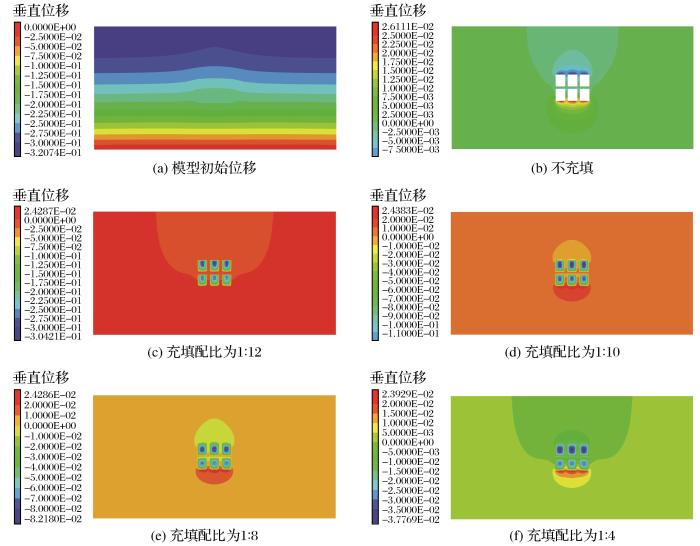
在不同充填配比下使用模型进行全过程模拟计算,最终得到垂直位移云图如图9所示。
图9
图9
不同配比充填体上覆岩层垂直位移云图
Fig.9
Vertical displacement contour maps of overlying rock with different backfill material ratios
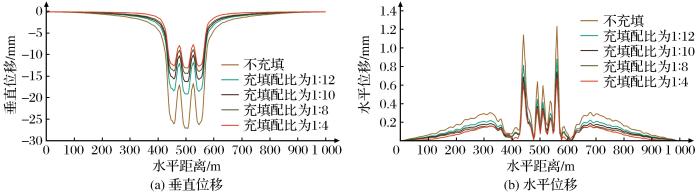
图10
图10
不同充填配比条件下覆岩垂直位移和水平位移
Fig.10
Vertical and horizontal displacements of overlying rock under different backfill ratios
由图10可知,位移变化曲线呈对称分布,垂直位移和水平位移随着充填配比的增加而显著减小。采空区不充填时,垂直位移和水平位移的最大值分别为-27.007 mm和1.232 mm;当以1∶12、1∶10、1∶8和1∶4的配比对采空区进行充填时,垂直位移分别减小至-19.078,-16.207,-14.320,-13.040 mm,水平位移分别减小至0.881,0.743,0.658,0.674 mm。
3.3 力学模型与数值模拟结果对比
表3 采场顶板最大下沉量计算结果对比
Table 3
| 充填配比 | 采空区顶板沉降/mm | 差异率/% | |
|---|---|---|---|
| 力学模型 | 数值模拟 | ||
| 1∶4 | -12.389 | -13.040 | 5.25 |
| 1∶8 | -13.834 | -14.320 | 3.51 |
| 1∶10 | -15.260 | -16.207 | 6.21 |
| 1∶12 | -17.528 | -19.078 | 8.84 |
4 地下矿山充填开采覆岩移动控制与工业试验
4.1 地下矿山充填开采覆岩沉降控制技术
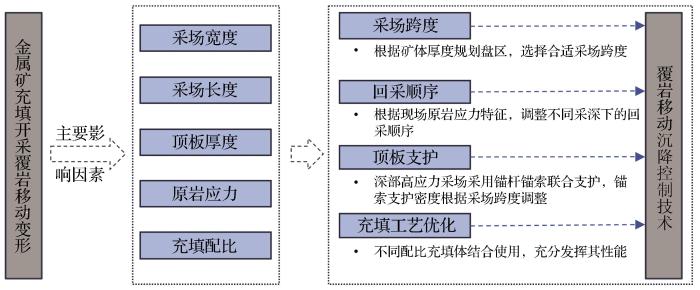
根据盘龙铅锌矿的实际开采技术条件,结合前文分析结果,可知影响充填开采上覆岩层移动变形的主要因素为采场宽度、采场长度、顶板厚度、原岩应力和充填体配比。据此建立覆岩沉降控制技术,具体原理如图11所示。
图11
图11
盘龙铅锌矿充填开采控制覆岩沉降基本原理
Fig.11
Basic principles of overlying rock settlement controlled by backfill mining in Panlong lead-zinc mine
选择合适的采场跨度是控制覆岩沉降的关键,若采场跨度过大,会导致爆破作业过程中顶板垮塌,危及作业人员安全;若采场跨度过小,回采效率过低,将影响矿山生产效益。其次,根据矿山原岩应力变化特征,适时调整回采顺序,也能在一定程度上降低覆岩移动。此外,顶板支护作为辅助手段,在结构面破碎或深部高应力采场宜采用锚杆+锚索联合支护,根据不同采场跨度,结合普氏平衡拱理论求得合适的锚索支护间距,可以有效防止爆破作业引起覆岩下沉导致顶板冒落。最后,根据不同配比下的充填体性能差异,结合盘龙铅锌矿技术条件,在一步骤采场采用1∶10的充填配比,底部胶面采用1∶8的配比,接顶部分采用1∶4的配比;在二步骤采场采用1∶12的充填配比,底部胶面和接顶部分的配比与一步骤采场相同。由以上分析可知,覆岩沉降控制技术基本原理主要围绕采矿开始至结束全过程控制,以达到减小上覆岩层移动变形和保护地表建筑物及人员作业安全的目的。
4.2 工业试验
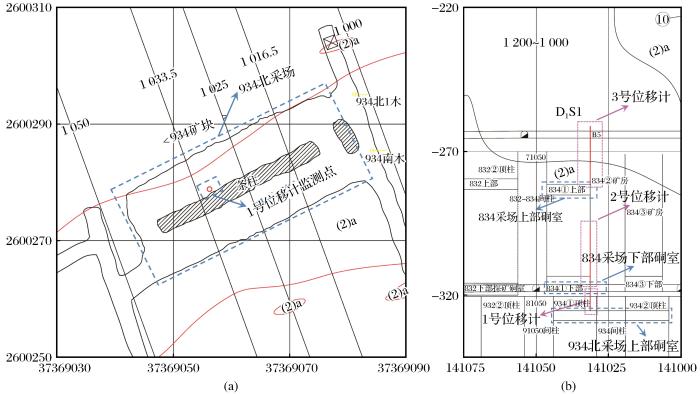
图12
图12
934北采场平面图(a)及位移监测点布置图(b)
Fig.12
Plan view of 934 north mining field (a) and layout of displacement monitoring points (b)
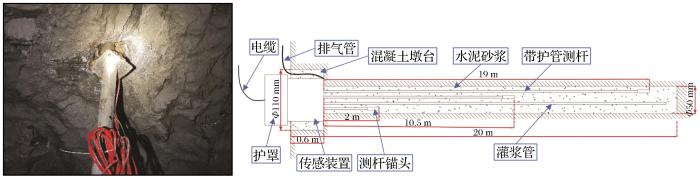
图13
图13
JTM-V7000J型振弦式多点位移计孔内安装示意图
Fig.13
Installation schematic diagram of JTM-V7000J vibrating wire multi-point displacement meter inside the hole
4.3 试验采场爆破块度及位移监测结果分析
观察试验采场下部出矿硐室矿堆照片(图14),结果显示岩石爆破块度适中,其中最大块径约为31 cm,未发现有明显大块,这不仅反映了爆破效果良好,同时表明采空区上覆岩层的移动变形得到了有效控制,未形成冒顶。
图14
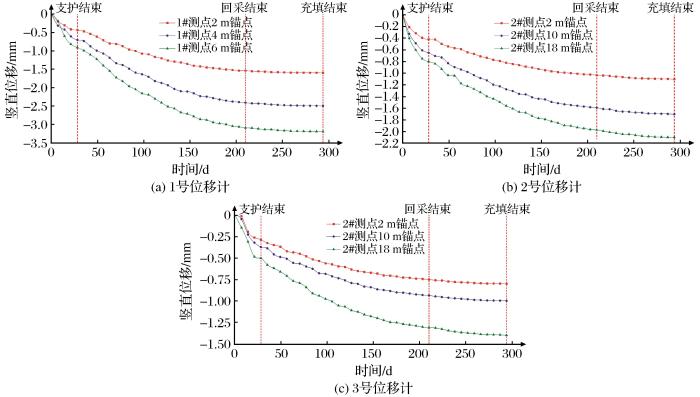
试验采场上覆岩层的位移时程曲线如图15所示,图中未支护条件下顶板沉降速度较快,3处测点初始顶板最大沉降速度分别为-0.065,-0.057,-0.038 mm/d。支护完成后顶板沉降速度显著缓解,3处测点的最大沉降速度分别为-0.022,-0.012,-0.008 mm/d。由此表明,与采空区距离越远的上覆岩层沉降位移越小,沉降速度越慢。最后,随着采空区的逐步充填,沉降速度逐渐趋近于0。直至全部充填完成,3处测点监测到的上覆岩层沉降最大值分别为-3.198,-2.095,-1.400 mm。这表明回采前进行锚杆+锚索联合支护,回采结束选择合适配比充填体进行胶结充填对于控制覆岩移动起到显著作用。试验采场的充填配比采用1∶10,顶板最大下沉为-3.198 mm,相较于表3中理论计算和数值模拟计算结果分别减小了79.04%和80.27%,说明本文覆岩沉降控制措施能够有效减少采场上覆岩层的位移沉降。
图15
图15
934北采场顶板沉降时程曲线
Fig.15
Time history curves of roof settlement in 934 north mining field
5 结论
通过建立充填开采覆岩移动非线性弹性地基梁力学分析模型,分析了不同影响因素下的覆岩移动特征,揭示了金属矿地下充填开采覆岩移动规律,结合数值模拟验证,最终形成金属矿充填开采覆岩沉降控制技术,得到的结论如下:
(1)基于地下金属矿山充填开采建立了非线性弹性地基梁力学分析模型,分析不同影响因素对覆岩移动的影响程度,发现充填体强度对顶板挠度和内力的影响最大。表明充填体强度是影响覆岩沉降的关键,提高充填体配比能显著减小上覆岩层位移。
(2)当充填体配比为1∶12、1∶10、1∶8和1∶4时,数值模拟计算得到顶板的最大沉降分别为-19.078,-16.207,-14.320,-13.040 mm,与非线性弹性地基梁力学模型的计算结果差异率在3%~9%之间,验证了非线性弹性地基梁力学模型对于金属矿山岩层移动计算的适用性和可靠性。
(3)提出了综合采场跨度、回采顺序、顶板支护和充填工艺优化的岩层控制技术并应用于工业试验,根据现场监测到的上覆岩层最大沉降值相较于理论计算和数值模拟计算结果分别减小了79.04%和80.27%,验证了地下矿山充填开采覆岩沉降控制技术的有效性和可行性。
http://www.goldsci.ac.cn/article/2024/1005-2518/1005-2518-2024-32-4-640.shtml
参考文献
Sudden surface collapse disasters caused by shallow partial mining in Datong coal field,China
[J].
Study on seam inclination based mining subsidence model and its visualized application with GIS
[J].
Roof movement and failure behavior when mining extra-thick coal seams using upward slicing longwall-roadway cemented backfill technology
[J].
Research on Strata Movement Rule and Control in Deep Solid Backfilling Mining
[D].
Study of non-proportional strength reduction method based on Hoek-Brown failure criterion
[J].
Application of Refined GSI Geological Model in Slope Stability Analysis and Research
[D].
Study on aluminum mining under coal and uniform settlement control technology of overlying rock
[J].
Assessment of ground subsidence hazard near an abandoned underground coal mine using GIS
[J].
Roof Movement Analysis in the Backfill Mining Area Based on Nonlinear Elastic Foundation Beam
[D].
Analytical prediction for tunneling-induced ground movements in clays
[J].
Study on safety thickness of layered-roof based on improved Protodyakonov equilibrium arch theory
[J].
Study on Collaborative Mining Theory and Roof Strata Mechanical Behavior of Deep Gently Inclined Medium-Thick Orebody
[D].
Temporal and Spatial Evolution Law of Mining Fissures in Thick Sandstone Roof and Evaluation of Water Inrush Risk
[D].
Performance of tunnel support un-der large deformation static and dynamic loading
[J].
Activity rules of overlying rock strata in mining areas and their influence on mine pressure
[J].
Comprehensive management scheme of geological hazards and ecological environment in coal mining subsidence areas
[J].
An innovative strata movement model for predicting overlying strata deformations
[J].
Study on the Non-linear Prediction Theory of Old Goaf Residual Subsidence and Its Application
[D].
The Overburden and Surface Deformation Characteristics of Deep Coal Mine Filling Mining Considering the Residual Deformation of Old Goaf
[D].
Prediction of the heights of the water-conducting fracture zone in the overlying strata of shortwall block mining beneath aquifers in western China
[J].
Study on the effect of mined-out region on ground subsidence
[J].
Deformation movement and mine pressure of hard rock layers in mining areas
[J].
Study on the Laws of Overlying Strata Movement and Surface Subsidence in Wanghe Coal Mine Paste Filling
[D].
基于倾角变化的开采沉陷模型及其GIS可视化应用研究
[J].
深部固体充填开采岩层移动规律及控制研究
[D].
基于Hoek-Brown准则的非等比强度折减方法
[J].
精细化GSI地质模型在边坡稳定性分析研究中的应用
[D].
煤下铝上行开采工艺控制覆岩均匀沉降研究
[J].
基于非线性弹性地基梁的充填采场顶板运动研究
[D].
基于改进普氏平衡拱理论的层状顶板安全厚度研究
[J].
深部缓倾斜中厚矿体协同开采理论及顶板岩层力学行为研究
[D].
厚砂岩顶板采动裂隙发育时空演化规律及突水危险性评价
[D].
采场上覆岩层活动规律及其对矿山压力的影响
[J].
采煤塌陷区内地质灾害与生态环境的综合治理方案
[J].
老采空区残余沉降非线性预测理论及应用研究
[D].
顾及老采空区残余变形的深部煤矿充填开采覆岩及地表变形特征
[D].
采场上覆坚硬岩层的变形运动与矿山压力
[J].
王河矿膏体充填开采覆岩移动变形及地表沉陷规律研究
[D].








 甘公网安备 62010202000672号
甘公网安备 62010202000672号