矿山多级机站通风系统风机优化选型方法

doi:10.11872/j.issn.1005-2518.2024.04.138

矿山多级机站通风系统风机优化选型方法

钟德云^,¹^,², 刘雨龙^,², 王李管¹^,²

1.长沙迪迈科技股份有限公司，湖南长沙 410221

2.中南大学资源与安全工程学院，湖南长沙 410083

Optimization of Fan Selection for Multi-stage Fan Station Ventilation System in Mines

ZHONG Deyun^,¹^,², LIU Yulong^,², WANG Liguan¹^,²

1.Changsha DIMINE Co. , Ltd. , Changsha 410221, Hunan, China

2.School of Resources and Safety Engineering, Central South University, Changsha 410083, Hunan, China

通讯作者: 刘雨龙（2000-），男，河南郑州人，硕士研究生，从事智能通风研究工作。225512106@csu.edu.cn

收稿日期: 2024-05-21 修回日期: 2024-06-17

基金资助:

国家重点研发计划项目“超大型深井矿山高效绿色开采技术与智能装备”. 2022YFC2904105

Received: 2024-05-21 Revised: 2024-06-17

作者简介 About authors

钟德云（1990-），男，福建长汀人，博士后，从事智能通风和地质建模研究工作deyizhiyun@163.com , E-mail：deyizhiyun@163.com

摘要

为了确定多级机站风机的最优不平衡风压分配方式，提出了一种以通风风机功率最小、最佳匹配风机风量和最佳匹配风机风压为目标的多级机站风机优选多目标优化模型，可用于确定各装机点所需的优选风机型号及风机安装角度。该模型既获得了近似满足风量要求的优选方案，也避免了非线性模型求解不收敛的问题，并在大规模多级机站通风系统中表现出高效的求解能力。此外，提出的多风机优选方法通过数学模型构建各级机站之间的相互约束关系，在风机工况范围内约束各装机点的不平衡风压，以解决各级机站风机风压合理分配的问题，避免因风机风压分配不合理导致风机选型失败。实例验证结果表明本研究的多级机站通风系统风机选型方案是可靠的。

关键词： 矿井通风 ; 多级机站通风系统 ; 风机优选 ; 通风优化 ; 多风机选型 ; 多目标优化

Abstract

The utilization of multi-stage fan station ventilation technology is crucial in the ventilation system of non-coal mines，particularly as mining depths increase.Traditional large main fan ventilation methods may struggle to adequately meet the ventilation requirements of deep mining operations，highlighting the significance of this technology.The multi-stage fan station ventilation system allows for the precise control of air volume and pressure in individual partitions by adjusting the operational status of fans at each level of the station.This method enhances the precision of adjustment and flexibility of control in the ventilation system，increases its efficiency，and decreases energy consumption.The conventional fan optimization approach assumes that each circuit accommodates only one air volume branch.In contrast，the ventilation network solution method utilizes the fan as a residual tree branch，enabling the direct allocation of unbalanced air pressure （fan pressure） to the residual tree branches of each autonomous circuit for fan optimization.In a multi-fan multi-stage station ventilation system，a single circuit may contain multiple installed air volume branches，rendering the traditional fan optimization method ineffective.Therefore，it is necessary to develop a fan optimization method suitable to multi-stage fan stations.Furthermore，due to the mutual influence between the installed branches in the multi-fan multi-stage fan station ventilation fan system，it is necessary to further consider the logical problem of air volume between the installed branches and the optimal allocation of unbalanced wind pressure（fan pressure）.In order to determine the optimal unbalanced wind pressure distribution method for multi-stage fan station，this study proposed a multi-objective optimization model for fan selection of multi-stage fan stations，aimed at achieving the minimum fan power consumption while optimizing the fan air volume and pressure.The proposed model assists in determining the most suitable fan model and installation angle for each installation point.The model successfully achieves the optimal solution that closely aligns with the air volume requirements，while also circumventing the issue of non-convergence in nonlinear model solutions.Additionally，it demonstrates efficient solution capabilities in large-scale，multi-stage fan station ventilation systems.Furthermore，the multi-fan optimization method proposed in this study establishes a mutual constraint relationship between stations at each level using a mathematical model.This approach ensures that the unbalanced wind pressure at each installation point remains within the operational range of the fan，thereby addressing the issue of distributing fan pressure effectively across all levels of the station and preventing fan selection failure due to improper pressure distribution.The reliability of the fan selection scheme for the multi-stage fan station ventilation system is confirmed through example verification in this research.

Keywords： mine ventilation ; multi-stage fan station ventilation system ; fan optimization ; ventilation optimization ; multi-fan selection ; multi-objective optimization

PDF (986KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

钟德云, 刘雨龙, 王李管. 矿山多级机站通风系统风机优化选型方法[J]. 黄金科学技术, 2024, 32(4): 666-674 doi:10.11872/j.issn.1005-2518.2024.04.138

ZHONG Deyun, LIU Yulong, WANG Liguan. Optimization of Fan Selection for Multi-stage Fan Station Ventilation System in Mines[J]. Gold Science and Technology, 2024, 32(4): 666-674 doi:10.11872/j.issn.1005-2518.2024.04.138

多级机站通风是一种可用于深部复杂矿山通风系统的技术，旨在有效解决矿山开采深度增加所带来的通风难题。相比传统的大主扇通风系统，多风机多级机站通风系统通过多级风机的级联策略，极大地提升了通风系统的调节精度和控制灵活性，能够显著提高通风系统效率，降低通风能耗，在非煤矿山得到普遍应用。

多级机站通风方式采用多级风机来动态调节各需风点的风量分配，改善井下风压分布状态，具有风量调节灵活、风压分布均匀和有效风量率高等特点（刘杰等，2010；贾安民，2012），在地下金属矿山得到了较广泛的应用。相比通风构筑物调节方式，采用风机来控制通风网络的风量分配，能够提高通风系统的可控性（陈喜山等，2002）。通过增设多级机站可以更容易地分配局部风流，减少总进回风量。然而，风机数量越多，风机智能监控的难度越大，智能通风对于风机智能监控子系统的要求也更高。陈宜华等（2008）分析了多级机站通风系统的设计方法。赖明照等（2016）通过三维通风系统仿真方式来优化多级机站通风系统。相关学者分析了多风机联合运转相互干扰可能导致的风机不稳定运转或风机负压运转问题（王桂坤，2008；孙星等，2009）。吴兴校（2018）针对现有风机监控系统评判不全面的问题，对大型矿井风机智能监控系统的实时安全评判策略和风机实时故障诊断方法进行了研究，从而提高了矿井通风系统运行的安全性。矿井智能通风系统的核心技术是实现井下按需通风，鉴于此，学者们对按需通风关键理论与技术（卢新明等，2020）和按需通风的初步实现方法（周福宝等，2020）等进行了研究，并指出智能通风应建立虚实映射模型（刘剑，2020）。相比增阻调节的按需调控方式，采用风机变频按需调控技术对于多级机站通风系统实现节能调控和按需分风效果更明显。然而，与风流调控优化问题（Ueng et al.，1984；Wang，1984）一样，风量未知的风机优选数学模型存在非线性项、求解较为困难的问题，一般需要采用禁忌搜索（Drezner et al.，1999；Stepanenko et al.，2007）、蚁群算法（Liang et al.，2018）和遗传算法（Lowndes et al.，2005；Kozyrev et al.，2012）等智能优化方法进行求解计算，且难以处理大规模复杂通风网络模型的风机优选问题。

由于多风机多级机站通风系统中各装机分支（装机点所在巷道）之间相互影响，传统风机优选方法并不适用，亟需研究一种适用于多级机站的风机优选方法。在风量分配计算过程中，对于单个回路最多只包含一条装机风量分支的情况，可以直接将风机作为余树分支，并将不平衡风压（风机风压）直接分配在各个独立回路的余树分支上进行风机优选。然而，对于单个回路可能存在多条装机风量分支的情况，则需要考虑装机分支之间风量的逻辑性问题和不平衡风压（风机风压）的优化分配问题。为了解决各级机站风机选型中风压相互影响的问题，本文提出了一种以通风风机功率最小、各级机站负压均衡、最佳匹配风机风量和最佳匹配风机风压为目标的多级机站风机优选多目标优化方法。

1 多级机站风机选型问题分析

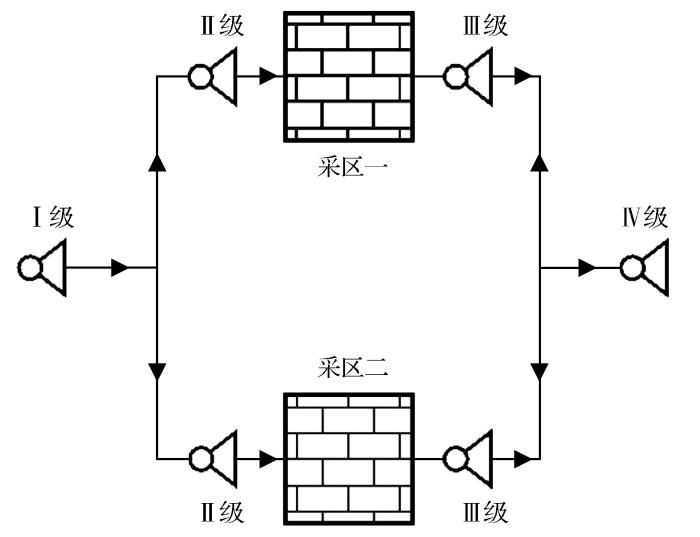
对于大主扇通风系统，可采用通风网络解算方法来确定风机安装位置的不平衡风压值，因此在风机优选时，可直接从备选风机库中进行比对选型。针对大主扇通风系统的传统风机优选方法，由于单个回路最多包含一条固定风量类型的装机风量分支，因此通风网络解算方法可将所有不平衡风压（风机风压）集中分配在固定风量类型的余树分支上。然而，对于多级机站通风系统，单个回路中往往包含多条固定风量类型的装机风量分支，传统的风机优选方法不再适用。图1所示为4级类型的多级机站通风系统。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 多级机站风机通风示意图

Fig.1 Schematic diagram of multi-stage fan station ventilation

相比传统的风机优选过程，多级机站风机优选需要处理不平衡风压、风压再分配的问题，其原因是多级机站通风网络装机风量分支之间的风机风压相互影响。若装机位置设置不合理或不平衡风压分配不合理，可能会出现部分风机装机风压不在合理范围之内，进而导致无法进行风机选型。

对于多风机多级机站通风系统，需要改进适用于多级机站通风网络的固定风量解算方法。采用固定风量解算法来确定通风网络分支风量的初始分配状态，以及装机分支不平衡风压的初始分布状态。在独立回路圈划时，一般要求每一独立回路只能包含一条固定风量巷道或装机巷道，且定流巷道总数不大于独立回路数，否则回路圈划无法进行。因此，在固定风量解算时，若一个回路中含有2条以上的定流巷道，就必须将生成树中的定流巷道暂时转化为非定流巷道，以保证解算过程的顺利进行。当通风网络分支风量的初始分配状态和装机分支不平衡风压的初始分布状态确定后，可采用风机优选数学模型来确定多级机站风机的最优不平衡风压分配方式。

多风机多级机站风机选型过程包括以下3个步骤：（1）根据装机分支装机风量的范围，按用户设置的风量间隔来确定多组装机风量值，采用固定风量解算法对分组装机风量值进行通风网络解算，初步确定通风网络风量分配初始状态和装机分支调节风压值。（2）采用多级机站风机优选数学模型来确定装机分支调节风压值，得到装机位置风机的装机风量和装机风压。（3）以装机位置风机的装机风量和装机风压为基础，按照风机运行效率等约束要求从数据库中进行匹配搜索，确定备选风机。对不同分组装机风量值优选得到的备选风机进行比较，确定最佳风机选型方案，辅助人工完成关于井下巷道装机位置处需要安装风机的最佳型号和风机安装角度的决策。

2 多级机站风机优选目标与约束条件

2.1 优选目标

多级机站风机优选的目标主要是优选可以满足井下各装机点风量通风需求（装机风量）和风压负载要求（装机风压）的最佳风机型号。为了实现井下按需调控和节能调控，并使各风机预留足够风量调控范围，多级机站风机优选应构造通风风机功率最小、同级机站负压均衡、最佳匹配风机风压和最佳匹配风机风量等多目标约束条件。

多级机站风机优选数学模型的多目标函数可表示为

$m i n Z = ω_{1} z_{1} + ω_{2} z_{2} + ω_{3} z_{3} + ω_{4} z_{4}$

（1）

式中： $z_{1}$ 为通风风机功率最小目标； $z_{2}$ 为同级机站负压均衡目标； $z_{3}$ 为最佳匹配风机风压目标； $z_{4}$ 为最佳匹配风机风量目标； $ω_{1}$ 为通风风机功率最小目标的权重系数； $ω_{2}$ 为同级机站负压均衡目标的权重系数； $ω_{3}$ 为最佳匹配风机风压目标的权重系数； $ω_{4}$ 为最佳匹配风机风量目标的权重系数。

（1）通风风机功率最小目标。最小目标函数可表示为

$z_{1} = \sum_{f \in F} q_{f} h_{f}$

（2）

式中： $F$ 为所有风机分支 $f$ 的集合，包括主扇和辅扇； $q_{f}$ 为风机分支 $f$ 的风机风量； $h_{f}$ 为风机分支 $f$ 的风机风压。

（2）各级机站负压均衡目标。均衡目标函数可表示为

$z_{2} = \sum_{f \in F} (d_{f}^{+} + d_{f}^{-})$

（3）

式中： $d_{f}^{+}$ 为各级机站中装机点 $f$ 装机风压与基准装机点 $f^{'}$ 装机风压的正偏差变量； $d_{f}^{-}$ 为各级机站中装机点 $f$ 装机风压与基准装机点 $f^{'}$ 装机风压的负偏差变量。

当根据装机风量大小按比例确定机站负压时， $d_{l k}^{+}$ 和 $d_{l k}^{-}$ 满足以下约束条件：

$\{\begin{matrix} h_{f^{'}} - \frac{q_{f^{'}}}{q_{f}} h_{f} - d_{f}^{+} + d_{f}^{-} = 0 \\ d_{f}^{+} \geq 0 \\ d_{f}^{-} \geq 0 \end{matrix}$

（4）

同级机站负压均衡目标函数可表示为

$z_{2} = \sum_{l = 1}^{L} \sum_{k = 1}^{K - 1} (d_{l k}^{+} + d_{l k}^{-})$

（5）

式中： $L$ 为多级机站的级数； $K$ 为同级机站的装机点数； $d_{l k}^{+}$ 为 $l$ 级机站中装机点 $k$ 装机风压与装机点 $K$ 装机风压的正偏差变量； $d_{l k}^{-}$ 为 $l$ 级机站中装机点 $k$ 装机风压与装机点 $K$ 装机风压的负偏差变量。

其中， $d_{l k}^{+}$ 和 $d_{l k}^{-}$ 满足以下约束条件：

$\{\begin{matrix} h_{l K} - h_{l k} - d_{l k}^{+} + d_{l k}^{-} = 0 \\ d_{l k}^{+} \geq 0 \\ d_{l k}^{-} \geq 0 \end{matrix}$

（6）

（3）最佳匹配风机风压目标。该目标函数可表示为

$z_{3} = \sum_{f \in F} ∆ h_{f}$

（7）

式中： $∆ h_{f}$ 为第 $f$ 条分支（装机分支）最佳风机风压范围偏差。

第 $f$ 条分支（装机分支）最佳风机风压范围偏差可表示为

$∆ h_{f} = \{\begin{matrix} h_{f, m i n} - h_{f}, h_{f} < h_{f, m i n} \\ 0, h_{f, m i n} \leq h_{f} \leq h_{f, m a x} \\ h_{f} - h_{f, m a x}, h_{f} > h_{f, m a x} \end{matrix}$

（8）

式中： $h_{f, m i n}$ 为第 $f$ 条分支（装机分支）最佳风机风压下限，满足 $h_{f, m i n} > 0$ ； $h_{f, m a x}$ 为第 $f$ 条分支（装机分支）最佳风机风压上限，满足 $h_{f, m a x} \geq h_{f, m i n} > 0$ 。

当要求实际风机风压不小于设定风压时，风机风压约束为

$h_{f, m a x} ≫ ∆ h_{f} = h_{f, m i n} > 0$

（9）

式中： $q_{j, n}$ 为第 $j$ 条分支（按需分风分支）的需风量。

当要求实际风机风压不大于设定风压时，风机风压约束为

$h_{f, m a x} = ∆ h_{f} ≫ h_{f, m i n} > 0$

（10）

当要求实际风机风压近似等于设定风压时，风机风压约束为

$h_{f, m a x} \approx ∆ h_{f} \approx h_{f, m i n} > 0$

（11）

为便于求解数学模型，最佳匹配风机风压目标需转化为

$m i n z_{3} = \sum_{f \in F} (\bar{h_{f}} + \underset{̲}{h_{f}})$

（12）

式中： $\bar{h_{f}}$ 为第 $f$ 条分支（装机分支）最佳风机风压范围上限偏差量； $\underset{̲}{h_{f}}$ 为第 $f$ 条分支（装机分支）最佳风机风压范围下限偏差量。

$\bar{h_{f}}$ 满足以下条件：

$\{\begin{matrix} ∆ h_{f} - \bar{h_{f}} \leq h_{f, m a x} \\ \bar{h_{f}} \geq 0 \end{matrix}$

（13）

$\underset{̲}{h_{f}}$ 满足以下条件：

$\{\begin{matrix} ∆ h_{f} + \underset{̲}{h_{f}} \geq h_{f, m i n} \\ \underset{̲}{h_{f}} \geq 0 \end{matrix}$

（14）

在以上条件的约束下，存在 $\bar{h_{f}}$ 和 $\underset{̲}{h_{f}}$ 必有一个为0的隐式约束条件。当该分支风机风压分配值处于最佳风机风压范围时，最佳风机风压范围上限偏差量 $\bar{h_{f}}$ 和最佳风机风压范围下限偏差量 $\underset{̲}{h_{f}}$ 均为0。

（4）最佳匹配风机风量目标。该目标函数可表示为

$z_{4} = \sum_{f \in F} ∆ q_{f}$

（15）

式中： $∆ q_{f}$ 为第 $f$ 条分支（装机分支）最佳风机风量范围偏差。

第 $f$ 条分支（装机分支）最佳风机风量范围偏差可表示为

$∆ q_{f} = \{\begin{matrix} q_{f, m i n} - q_{f}, q_{f} < q_{f, m i n} \\ 0, q_{f, m i n} \leq q_{f} \leq q_{f, m a x} \\ q_{f} - q_{f, m a x}, q_{f} > q_{f, m a x} \end{matrix}$

（16）

式中： $q_{f, m i n}$ 为第 $f$ 条分支（装机分支）最佳风机风量下限，满足 $q_{f, m i n} > 0$ ； $q_{f, m a x}$ 为第 $f$ 条分支（装机分支）最佳风机风量上限，满足 $q_{f, m a x} \geq q_{f, m i n} > 0$ 。

同理，最佳匹配风机风量目标函数需转化为

$m i n z_{4} = \sum_{f \in F} (\bar{q_{f}} + \underset{̲}{q_{f}})$

（17）

式中： $\bar{q_{f}}$ 为第 $f$ 条分支（装机分支）最佳风机风压范围上限偏差量； $\underset{̲}{q_{f}}$ 为第 $f$ 条分支（装机分支）最佳风机风压范围下限偏差量。

$\bar{q_{f}}$ 满足以下条件：

$\{\begin{matrix} q_{f} - \bar{q_{f}} \leq q_{f, m a x} \\ \bar{q_{f}} \geq 0 \end{matrix}$

（18）

$\underset{̲}{q_{f}}$ 满足以下条件：

$\{\begin{matrix} q_{f} + \underset{̲}{q_{f}} \geq q_{f, m i n} \\ \underset{̲}{q_{f}} \geq 0 \end{matrix}$

（19）

2.2 约束条件

（1）风量平衡约束。根据风量平衡定律，建立数学模型约束条件：

$\sum_{j = 1}^{N} a_{i j} q_{j} = 0, i = 1,2, \dots, J$ -1

（20）

式中： $J$ 为通风网络的节点数； $a_{i j}$ 为节点与分支之间的关系。

其中， $a_{i j}$ 满足：

$a_{i j} = \{\begin{matrix} 0, 节点 i 与分支 j 不邻接 \\ - 1, 节点 i 与分支 j 邻接, 且 i 为分支末点 \\ 1, 节点 i 与分支 j 邻接, 且 i 为分支起点 \end{matrix}$

（2）风压平衡约束。根据风压平衡定律，建立数学模型约束条件：

$\sum_{j = 1}^{N} b_{i j} h_{j} = 0, i = 1,2, \dots, M$

（21）

式中： $M$ 为通风网络的独立回路数， $M = N - J + 1$ ； $h_{j}$ 为第 $j$ 条分支风压的代数和， $h_{j} = r_{j} q_{j}^{2} + ∆ h_{j} - h_{N, j}$ ； $r_{j}$ 为第 $j$ 条分支的风阻； $q_{j}$ 为第 $j$ 条分支的风量； $∆ h_{j}$ 为第 $j$ 条分支的风压调节值； $h_{N, j}$ 为第 $j$ 条分支的自然风压； $b_{i j}$ 为分支与回路之间的关系。

其中， $b_{i j}$ 满足：

$b_{i j} = \{\begin{matrix} 0, 分支 j 不在独立回路 i 内 \\ - 1, 分支 j 在独立回路 i 内, 且与回路反向 \\ 1, 分支 j 在独立回路 i 内, 且与回路同向 \end{matrix}$

（3）装机分支约束。不平衡风压只允许出现在装机分支中，且装机分支只能进行增能调节。因此，风压调节值应满足：

$\{\begin{matrix} ∆ h_{j} < 0, j \in F \\ ∆ h_{j} = 0, j \notin F \end{matrix}$

（22）

（4）风压调节范围约束。装机分支风机风压调节范围约束应满足：

$∆ h_{j, f m i n} \leq ∆ h_{j} \leq ∆ h_{j, f m a x}, j \in F$

（23）

式中： $∆ h_{j, f m i n}$ 为第 $j$ 条分支（装机分支）可调节风机风压下限； $∆ h_{j, f m a x}$ 为第 $j$ 条分支（装机分支）可调节风机风压上限。

（5）风机运转风量约束，应满足：

$q_{j, f m a x} \geq q_{j} \geq q_{j, f m i n}, j \in F$

（24）

式中： $q_{j}$ 为第 $j$ 条分支（装机分支）的风量（装机风量）； $q_{j, m i n}$ 为第 $j$ 条分支（装机分支）允许风机风量下限，满足 $q_{j, f m i n} \geq 0$ ； $q_{j, m a x}$ 为第 $j$ 条分支（装机分支）允许风机风量上限，满足 $q_{j, f m a x} \geq q_{j, m i n} \geq 0$ 。

（6）风机运转效率约束，应满足：

$η_{j} \geq C_{j}, j \in F$

（25）

式中： $η_{j}$ 为第 $j$ 条分支（装机分支）的风机运转效率； $C_{j}$ 为某个常数，表示第 $j$ 条分支（装机分支）要求的最低风机运转效率。

（7）风机运转参数约束。风机参数上下限约束条件要求选型风机的风机参数满足限定范围的条件，即：

$p_{j, f m a x} \geq p_{j} \geq p_{j, f m i n}$

（26）

式中： $p_{j, f}$ 为第 $j$ 条分支（装机分支）的风机参数（风机直径、转数、叶片安装角度和风机串并联数等）； $p_{j, f m i n}$ 为第 $j$ 条分支（装机分支）相应风机参数（风机直径、转数、叶片安装角度和风机串并联数等）允许数值的下限； $p_{j, f m a x}$ 为第 $j$ 条分支（装机分支）相应风机参数（风机直径、转数、叶片安装角度和风机串并联数等）允许数值的上限。装机分支的风机运转参数约束可以在比对风机库备选风机的风机特性曲线时确定。

3 多级机站风机优选数学模型

3.1 数学模型构建

为简化问题，本文仅考虑装机风量的已知约束条件，先确定装机位置的最佳风机风压，然后采用传统的风机优选方法，从风机优选库中筛选满足风机参数约束要求的所有备选风机。本文所构建的数学模型仅用于确定各级机站风机的调节风压，因此不用考虑风机参数相关的约束。

装机风量已确定的多级机站风机优选数学模型可表示为

$m i n Z = ω_{1} \sum_{f \in F} q_{f} h_{f} + ω_{2} \sum_{f \in F} (d_{f}^{+} + d_{f}^{-}) +$

$ω_{3} \sum_{f \in F} (\bar{h_{f}} + \underset{̲}{h_{f}})$

（27）

$s . t . \{\begin{matrix} \sum_{j = 1}^{N} b_{i j} h_{j} = 0, i = 1,2, \dots, M \\ \begin{array}{l} ∆ h_{j} < 0, j \in F \\ ∆ h_{j} = 0, j \notin F \end{array} \\ ∆ h_{j, f m i n} \leq ∆ h_{j} \leq ∆ h_{j, f m a x}, j \in F \\ ∆ h_{f} - \bar{h_{f}} \leq h_{f, m a x} \\ ∆ h_{f} + \underset{̲}{h_{f}} \geq h_{f, m i n} \\ h_{f^{'}} - \frac{q_{f^{'}}}{q_{f}} h_{f} - d_{f}^{+} + d_{f}^{-} = 0 \\ \bar{h_{f}} \geq 0 \\ \underset{̲}{h_{f}} \geq 0 \\ d_{f}^{+} \geq 0 \\ d_{f}^{-} \geq 0 \end{matrix}$

数学模型的决策变量为所有装机分支的调节风压值 $∆ h_{j}$ ，以及辅助决策变量 $\bar{h_{f}}$ 、 $\underset{̲}{h_{f}}$ 、 $d_{f}^{+}$ 和 $d_{f}^{-}$ 。由于已知风量可看作常量，目标函数和约束条件均为线性函数，相应的数学模型为线性规划模型。

3.2 数学模型求解

风机优选流程以装机位置风机的装机风量和装机风压为基础，按照风机运行效率等约束条件从数据库中进行匹配搜索，确定备选风机。

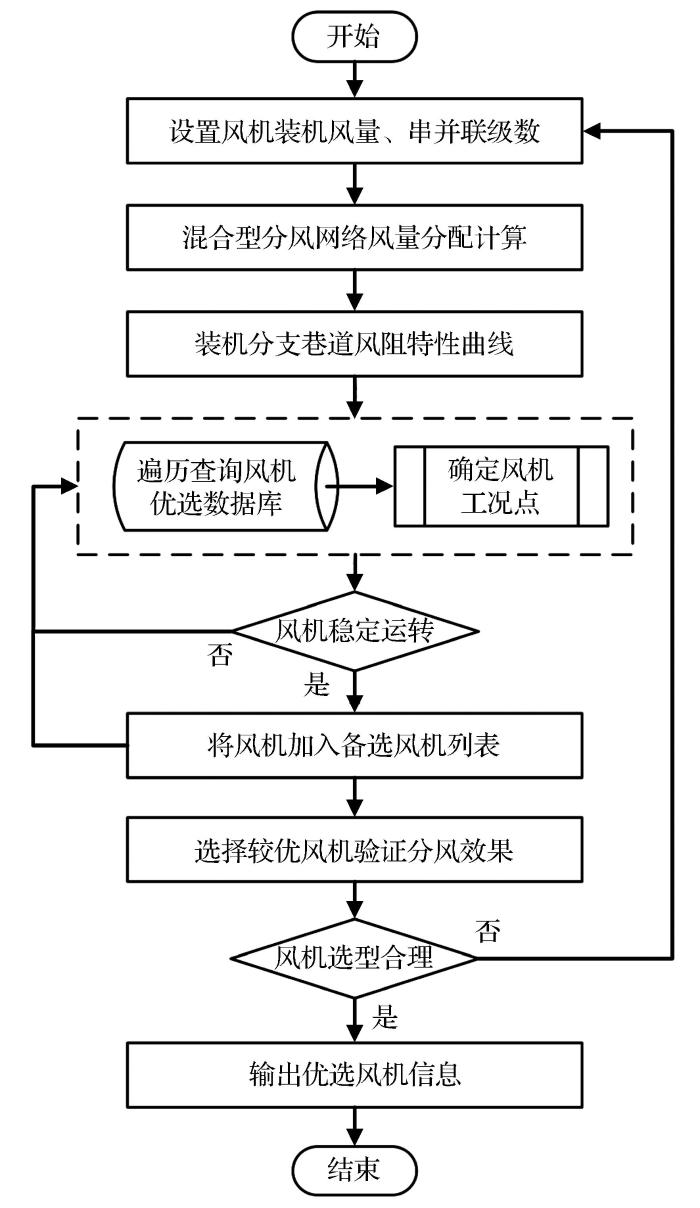
如图2所示，风机优选流程基本步骤如下：

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 风机优选流程图

Fig.2 Fan optimization flowchart

（1）在风机安装位置（装机风量分支）根据按需分风要求设置装机风量、风机串联运转或并联运转级数等参数。

（2）对混合型分风网络进行风量分配计算，确定装机风量分支不平衡风压值。

（3）计算装机分支的虚拟装机风量和虚拟装机风压，并确定装机分支处的巷道风阻特性曲线。

（4）根据装机分支处的巷道风阻特性曲线，逐个查询风机优选库中风机的风量—风压特性曲线，确定风机的工况点。

（5）若风机的工况点满足风机的运转效率不低于60%和风机工作风压不超过最高风压90%的条件，则将该风机加入备选列表。

（6）按不同方式对待选风机列表进行排序，并列出备选风机的风机类型、叶片角度、工况风量、工况风压、效率、电机功率和风机串并联级数等信息。

（7）结合矿山实际情况，用户选择一种较优的风机，将实际风机信息替换装机风量，重新对通风网络进行风量分配计算，验证所选风机的实际风量分配效果。

（8）若所选风机不合适，重新设置装机分支装机风量、风机串联运转或并联运转级数等参数，根据风机联合运转风量—风压特性曲线重新确定风机的工况点，并跳转至第5步重新确定备选风机。

4 多级机站风机优选计算实例

在早期研发的iVent三维矿井通风软件平台的基础上，采用C++编程语言实现了针对矿山多风机多级机站通风系统的风机优化选型算法，用户可以任意新增和修改多目标参数和约束条件，以便获得一组满足实际选型要求的满意解。

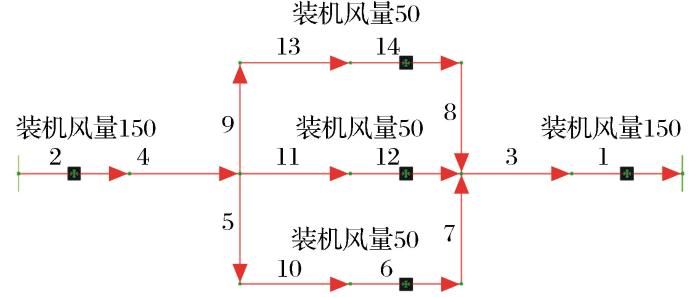
图3所示为一个简化的矿山通风网络图，用于验证多级机站风机优选方法的可靠性，图中数字为通风网络分支编号。该通风网络采用压—抽—压的三级机站通风方式，含有14条分支和13个节点，5个装机点位置。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 多级机站风机优选实例

Fig.3 Optimization example of multi-stage fan station

当结合矿山实际情况进行风机优选时，若必须从指定风机库中优选风机，在构造风机优选数学模型时，通常要考虑备选风机库信息得到的备选风机约束条件（装机分支风压调节范围约束和风机运行工况约束）。若装机分支对应的装机风量已经确定，可通过遍历风机库备选风机的方式初步确定装机风量相应的装机风压合理（可选）范围。

表 1 多级机站通风网络风量分配结果

Table 1 Airflow distribution results of multi-stage fan station ventilation network

风机编号	安装位置	风机类型	通风方式	长度/m	风阻/（N·s²·m^-8）	解算风量/（m³·s^-1）	调节风压/Pa
1	出风	装机	抽出式	30	0.033	150	-3 232.50
2	进风	装机	压入式	30	0.036	150	0.00
6	内部	装机	抽出式	30	0.030	50	0.00
12	内部	装机	抽出式	30	0.030	50	157.50
14	内部	装机	抽出式	30	0.030	50	15.00

新窗口打开| 下载CSV

表2 多级机站通风网络风压分配结果

Table 2 Wind pressure distribution results of multi-stage fan station ventilation network

风机编号	安装位置	风机类型	长度	风阻/（N·s²·m^-8）	解算风量/（m³·s^-1）	装机风量/（m³·s^-1）	装机风压/Pa
1	出风	装机	30	0.033	150	150	1 378.92
2	进风	装机	30	0.036	150	150	1 378.92
3	内部	非装机	30	0.030	150	-	-
4	内部	非装机	30	0.030	150	-	-
5	内部	非装机	30	0.024	50	-	-
7	内部	非装机	30	0.036	50	-	-
8	内部	非装机	30	0.033	50	-	-
9	内部	非装机	30	0.027	50	-	-
10	内部	非装机	30	0.042	50	-	-
11	内部	非装机	30	0.039	50	-	-
13	内部	非装机	30	0.036	50	-	-
6	内部	装机	30	0.030	50	50	474.64
12	内部	装机	30	0.030	50	50	317.14
14	内部	装机	30	0.030	50	50	459.64

新窗口打开| 下载CSV

为了采用多级机站风机优选数学模型对图3所示的通风网络进行风机优选，应先采用装机风量逻辑相关的固定风量解算法进行风量分配计算。表1~表3分别为该通风网络各级机站的风量、风压分配结果和风机优选结果，其中风机优选结果包含各装机点优选的风机型号及风机安装角度等信息。

表3 多级机站通风网络风机优选结果

Table 3 Fan optimization of multi-stage fan station ventilation network

风机编号	安装位置	风机类型	通风方式	风机型号	叶片角度	串联	并联
1	出风	装机	抽出式	DK40-8No26	-5°	1	1
2	进风	装机	压入式	DK40-8No26	-5°	1	1
6	内部	装机	抽出式	K40-8No21	20°	1	1
12	内部	装机	抽出式	K40-8No20	23°	1	1
14	内部	装机	抽出式	K40-8No21	20°	1	1

新窗口打开| 下载CSV

当确定通风网络各级机站风量分配和风压分配的结果后，可直接采用装机分支逻辑不相关的风机优选方法确定各装机点备选风机，为通风系统设计人员辅助决策。

5 结论

（1）本文提出的以通风风机功率最小、最佳匹配风机风量和最佳匹配风机风压为目标的多目标优化数学模型，可用于多级机站通风系统风机优选。该模型通过合理分配各级机站风机风压，为风机选型过程提供了最佳的风机工况参数，可用于确定各装机点满足井下通风需求的优选风机型号及风机安装角度。由于该模型为线性规划数学模型，且决策变量主要与通风网络中装机点的个数有关，因此该方法避免了非线性模型求解困难的问题且具有较高的求解效率，适用于大规模多级机站通风系统的风机优化选型。

（2）对于多级机站通风网络，单个独立回路中可能包含多条固定风量类型的装机风量分支，需要考虑多风机通风系统各级机站之间风机风压相互影响的问题。本文提出的多风机优选方法可以通过数学模型构造各级机站之间的相互约束关系，在风机工况范围约束下确定各装机点位置不平衡风压，可以解决各级机站风机风压合理分配的问题，避免因风机风压分配不合理导致风机选型失败。当确定各级机站风机风压之后，可以直接从备选风机库中匹配最佳的风机型号。

（3）类似于通风网络优化调控方法，风机装机位置和装机风量可变的风机优选数学模型，由于非线性模型求解困难的问题难以找到合适的风机选型方案。本文在两步骤通风优化方法的基础上，通过多次给定不同装机位置及相应装机风量的方式来构造线性化的数学规划模型，将非线性数学模型进行线性化求解，以避免非线性模型求解困难的问题。尽管该方法需要预先确定装机点位置和装机风量，但通过多次给定风机装机方案进行线性求解，可以得到类似非线性模型的优选方案，以及处理复杂多级机站通风系统多风机选型问题。

http://www.goldsci.ac.cn/article/2024/1005-2518/1005-2518-2024-32-4-666.shtml

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[]

Chen

Xishan

， Liang

Xiaochun

， Li

Yang

，2002.

Multi-stages ventilation arrangement and new development of ventilation technology in underground metallic ore mines

［J］.China Ming Magazine，（5）：13-15.

Chen

Yihua

， Sun

Huoran

，2008.

Research on optimization design method for mine multi-stage fan station ventilation system

［J］.Metal Mine，37（1）：121-124.

Drezner

， Marcoulides

G A

， Salhi

，1999.

Tabu search model selection in multiple regression analysis

［J］.Communications in Statistics-Simulation and Computation，28（2）：349-367.