地下矿扇形中深孔装药设计模型研究与应用

doi:10.11872/j.issn.1005-2518.2024.06.060

地下矿扇形中深孔装药设计模型研究与应用

陈鑫^,

长沙迪迈科技股份有限公司，湖南长沙 410083

Research and Application of Model for Fan-shaped Medium-deep Hole Charging Design in Underground Mines

CHEN Xin^,

DIMINE Co. ，Ltd. ，Changsha 410083，Hunan，China

收稿日期: 2024-03-01 修回日期: 2024-07-01

Received: 2024-03-01 Revised: 2024-07-01

作者简介 About authors

陈鑫（1990-），男，安徽合肥人，博士，高级工程师，从事数字矿山研究工作whutcx@163.com , E-mail：whutcx@163.com

摘要

为解决地下矿扇形中深孔装药设计过程中人机交互设计存在的主观性大、炮孔装药能量无法均匀分布和装药效果难以定量评估等问题，提出了一种地下矿扇形中深孔装药设计数学模型。总体思路为：结合爆破边界空间约束和爆破参数要求，运用参数化装药设计思想构建地下矿扇形中深孔装药设计数学模型，采用运筹学方法解算数学模型得到最优化装药设计。研究成果在数字采矿软件平台中开发实现，并将构建的装药优化模型用于某地下矿扇形中深孔装药设计。试验结果表明，相似地质条件和装药条件下，2次爆破试验中，采用参数化装药设计现场出矿大块率明显低于人机交互式装药设计，装药设计时间极大地缩短，从4 h减少至5 min。地下矿扇形中深孔装药设计优化方法极大地减少了设计技术人员工作量，最大程度地保障了炮孔间装药能量分布均匀性，有效提高了爆破质量。

关键词： 数字化采矿 ; 扇形中深孔 ; 爆破装药设计 ; 数学模型 ; 参数化

Abstract

In the context of underground mining in metal mines，perforated blasting constitutes a critical component of the operational process.Currently，the design of fan-shaped medium-deep hole blasting charges involves considerable repetitive tasks.Manual interactive adjustments merely satisfy the fundamental design requirements，resulting in significant subjective variability.Both domestic and international scholars have conducted extensive research on the design methodologies for medium-deep hole charges in underground mining.Regarding the application of the empirical rule formula，experts have undertaken comprehensive research on the ring blasting load spacing in underground stopes，optimizing drilling and blasting parameters to furnish a scientific foundation for blasting operations in subterranean mines.In the context of CAD auxiliary tools，certain scholars have employed Visual Lisp and other programming tools to enhance CAD’s secondary development capabilities，thereby enabling the automated design of sector medium-deep hole charges.In the domain of numerical simulation，the parameters are established through an integration of blasting tests and LS-DYNA numerical simulation analysis，leading to the effective optimization of design parameters for fan-shaped medium-deep hole blasting.Regarding intelligent algorithm research，enhanced extreme learning machine （ELM），backpropagation（BP） neural networks，and other algorithms are employed to construct a blasting design model，facilitating the intelligent determination of blasting parameters and optimization of charge. Nonetheless，these methodologies are relatively simplistic and donot incorporate the principles of systems engineering.Therefore，this paper investigated the integration of system engineering optimization methods with the application of blasting design engineering，specifically focusing on the parametric design methodology for medium-deep hole charges in the context of underground mining.The overarching approach is as follows：By considering the spatial constraints of the blasting boundary and the requisite blasting parameters，a mathematical model was formulated based on the principles of parametric charge design.This model was subsequently solved using operations research techniques to derive the optimal charge design.The research findings were developed and implemented using a digital mining software platform.The formulated charging optimization model was applied to the charging design of medium-deep boreholes in an underground mining context.The results indicate that the proportion of ore fragments in the field，when utilizing the parameterized charging design，is significantly lower compared to the man-machine interactive charging design under analogous geological and charging conditions.The proposed method for optimizing the charging design of fan-shaped medium-deep holes in underground mines significantly reduces the workload of design technicians and maximizes the uniformity of energy distribution among the holes. This approach effectively enhances the quality of blasting operations.

Keywords： digital mining ; fan-shaped medium-deep holes ; blasting charge design ; mathematical model ; parameterization

PDF (2258KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

陈鑫. 地下矿扇形中深孔装药设计模型研究与应用[J]. 黄金科学技术, 2024, 32(6): 1107-1115 doi:10.11872/j.issn.1005-2518.2024.06.060

CHEN Xin. Research and Application of Model for Fan-shaped Medium-deep Hole Charging Design in Underground Mines[J]. Gold Science and Technology, 2024, 32(6): 1107-1115 doi:10.11872/j.issn.1005-2518.2024.06.060

在金属矿山地下开采过程中，穿孔爆破作业是其重要环节（袁节平等，2008；王辉林等，2012；程兵等，2023）。中深孔爆破技术被广泛应用于地下矿山开采，合理设计其装药结构能够极大地提高矿山生产效率，并有效保障矿山爆破作业质量及生产安全（杨恒涛，2017；王成龙等，2021；汪洋等，2022；骆浩浩等，2023；梁瑞等，2024）。目前扇形中深孔爆破设计工作存在大量人工重复操作。在装药设计过程中，需要根据炮孔分布情况、爆破参数和地质条件变化反复调整（赵艳伟等，2014；王平等，2015；刘猛，2017；周源，2019）。大量重复性装药设计计算工作费时费力，且在设计过程中，人机交互式调整装药仅能满足基本的爆破装药设计参数要求，主观随意性较大。

鉴于此，国内外学者对地下矿扇形中深孔装药设计方法进行了广泛而深入的研究。在经验公式优化领域，学者们深入探讨了地下采场环形爆破载荷的间距问题，通过优化钻孔和爆破参数，为地下矿山的爆破作业提供科学依据（Himanshu et al.，2021）。在CAD辅助工具应用方面，部分学者利用Visual Lisp等工具对CAD软件进行二次功能开发扩展，实现了扇形中深孔装药设计的自动化和高效化（周科平等，2017；刘益超等，2021）。在数值模拟分析方面，结合现场爆破试验和LS-DYN等数值模拟软件，对扇形中深孔爆破参数进行设计和优化，有效提升了爆破作业的安全性（Gao et al.，2023）。此外，在智能算法的探索中，利用改进极限学习机（ELM）和BP神经网络等算法，构建爆破设计模型，实现了爆破参数的智能化设定和装药优化调整（张耿城等，2021）。

综上所述，人机交互式设计、计算机模拟计算、参数自动化校准和成果优选等技术在爆破设计中展现出巨大的应用潜力和价值。然而，这些技术过于单一，并未体现系统工程学中的整体优化思想。鉴于此，本文将系统工程学中的最优化方法与爆破设计工程应用紧密结合，通过引入系统工程学的理论框架，深入探索并构建地下矿扇形中深孔装药参数化设计方法，以填补该研究领域的空白。

1 总体架构及思路

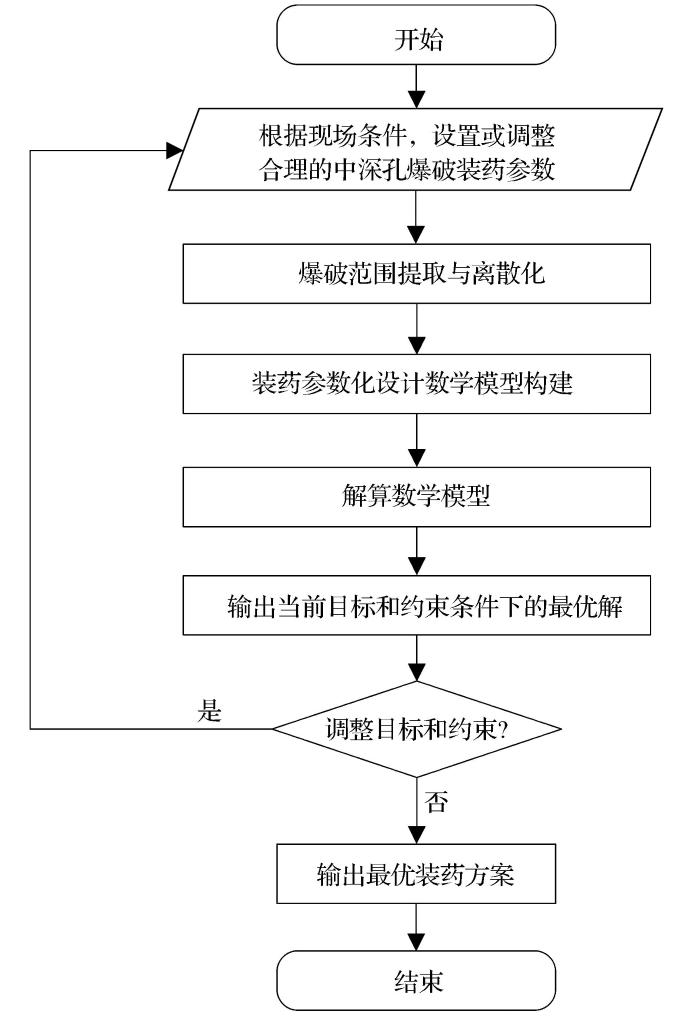
为进行地下矿扇形中深孔参数化装药设计，通过构建扇形中深孔装药数学模型，当模型接收到装药设计参数后，自动调整设计目标及约束条件，并重新求解获得最优设计成果。参数化装药设计方法总体流程如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 地下矿扇形中深孔装药设计方法总体流程

Fig.1 Overall flowchart of the charge design methodology for fan-shaped medium-deep hole in underground mines

1.1 设置扇形中深孔爆破装药参数

依据采场地质岩性、构造情况等工程条件，设置合理的扇形中深孔爆破装药参数。具体参数包括：最小填塞长度、装药影响半径、排间距、爆破范围面积、装药线密度、孔径、炸药单耗和离散化网格数量。

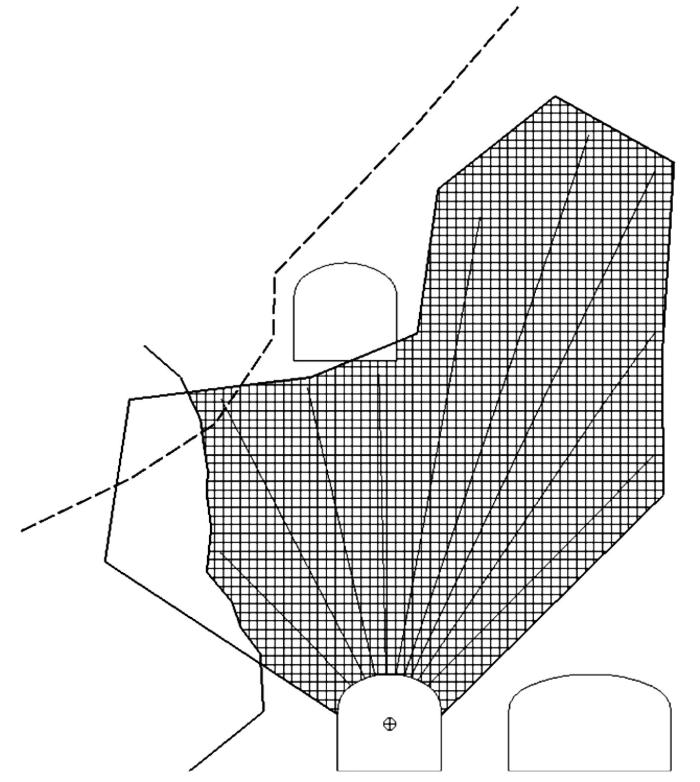
1.2 爆破范围提取与离散化

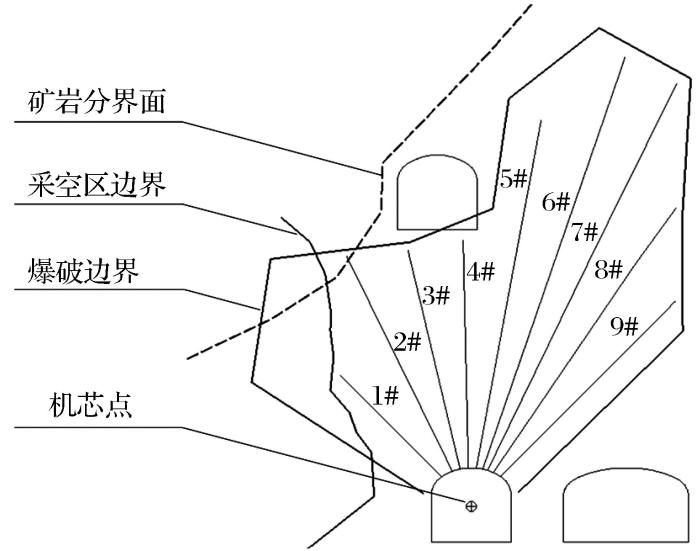
首先，根据矿岩分界面、采空区边界、爆破边界、巷道边界和机芯点位置的空间分布情况，提取所有矿岩分界面、采空区边界、爆破边界和巷道边界构成的最小闭环（夏红兵等，2008）。

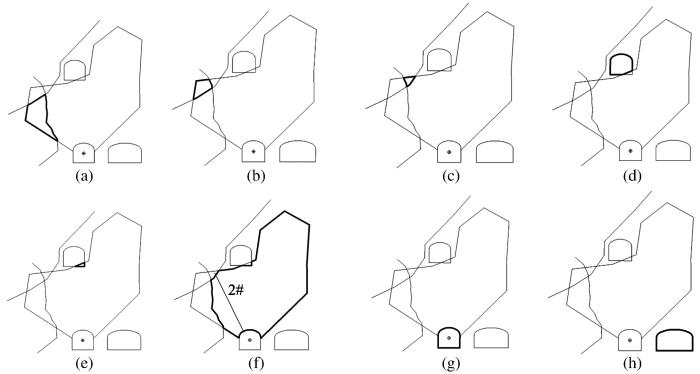
然后，对任意一个炮孔，当该炮孔与矿岩分界面、采空区边界、爆破边界、巷道边界的交点仅有1个时，选择该炮孔的中点所在的最小闭环为爆破范围；当该炮孔与矿岩分界面、采空区边界、爆破边界、巷道边界的交点大于1个时，选择该炮孔的起点与下一个交点的中点所在的最小闭环为爆破范围。

最后，按离散化单元尺寸对爆破范围进行离散化，爆破范围内所有离散化网格定义为离散化集合（张袁娟等，2013；郑炳旭等，2015）。

1.3 装药参数化设计数学模型构建

基于参数化设计思想构建起地下矿扇形中深孔参数化装药设计数学模型。将扇形中深孔装药设计作业参数化，输入装药参数条件。经计算机计算输出装药设计结果，实现装药设计过程自动化。模型包括：参数、集合、索引、决策变量、目标函数和约束条件等。

1.4 装药参数化设计数学模型解算

以VC++为开发工具，通过运筹学方法解算该地下矿扇形中深孔参数化装药设计数学模型。通过模型解算结果确定最优扇形中深孔参数化装药设计方案。

2 地下矿扇形中深孔参数化装药设计数学模型构建

2.1 模型构建

基于参数化设计思想构建了地下矿扇形中深孔参数化装药设计数学模型。数学模型参数包括：离散化网格单元（ $a$ ）、网格单元是否在炮孔装药影响半径内（x）、装药结构方案是否为最终装药结构（y）、担负矿量离散化网格（ $b$ ）、炮孔（ $h$ ）、炮孔孔深 $(e$ ）、最小填塞长度（ $d^{h m i n}$ ）、装药影响半径（ $d^{h r}$ ）、排间距（ $d^{c}$ ）、爆破范围面积（ $s^{b}$ ）、装药线密度（ $β^{l}$ ）、孔径（ $d^{r}$ ）、炸药单耗（ $β^{b}$ ）和离散化网格尺寸（m×n）。

集合包括：爆破单位内离散化网格集合（A）、担负矿量关系集合（ $B$ ）、炮孔集合（H）、炮孔孔深集合（E）、炮孔装药结构方案集合（ $F$ ）和炮孔装药结构方案的装药长度集合（ $S$ ）。

集合的索引包括：离散化网格索引（i、k）；炮孔的索引（j），装药结构方案索引（p）。

决策变量包括：

x_{i} = \{\begin{matrix} 1, 离散 化网 格 a_{i} 在炮 孔装 药结 构影 响半 径范 围内 \\ 0, 离散 化网 格 a_{i} 不在 炮孔 装药 结构 影响 半径 范围 内 \end{matrix}

（1）

y_{j, p} = \{\begin{matrix} 1, 第 j 个炮 孔的 第 p 种装 药结 构方 案为 最终 装药 结构 \\ 0, 第 j 个炮 孔的 第 p 种装 药结 构方 案非 最终 装药 结构 \end{matrix}

（2）

目标函数：Max $\sum_{i} x_{i}$

约束包括：

决策变量逻辑性约束：

x_{i} = 0 或 1, \forall i \in A

（3）

y_{j, p} = 0 或 1, \forall j \in H, p \in F_{j}

（4）

炮孔j有且仅有一个装药结构方案为最终装药结构，表示为

\sum_{p} y_{j, p} = 1

（5）

装药与担负矿量关系约束：

x_{j, p, k} \leq y_{j, p}, \forall j \in H, p \in F_{j}, k \in B_{j}

（6）

其中， $B_{j}$ 中的离散化网格 $b_{j, k}$ 的质心与炮孔 $h_{j}$ 装药结构的最小距离小于 $d^{h r}$ 。

炮孔间装药结构互斥性约束：

y_{j, p} \times y_{j^{'}, p^{'}} = 0, \forall j, j^{'} \in H, p \in F_{j}, p^{'} \in F_{j^{'}}

，若

y_{j, p}

与

y_{j^{'}, p^{'}}

装药结构互斥（7）

总装药量与炸药单耗匹配约束：

\sum_{j} \sum_{p} s_{j, p} \times y_{j, p} \times β^{l} = s^{b} \times d^{c} \times β^{b}

（8）

2.2 模型分析

基于参数化设计思想构建了地下矿扇形中深孔参数化装药设计数学模型。模型的目标是确保在各项约束条件下装药结构的影响范围最大。

模型包括多个约束条件。其中，式（3）~式（4）为决策变量逻辑约束。式（3）确保了决策变量x_i 只能取0或1，即离散化网格单元必然位于炮孔装药结构影响范围内；式（4）确定了各炮孔的各可行装药结构方案必然是或不是最终装药结构方案。式（5）为单炮孔最终装药方案数约束，即单个炮孔有且仅有一个最终装药结构方案。式（6）为装药与担负矿量关系约束，即各炮孔的各可行装药方案对应担负矿量关系离散化网格在最终装药结构影响范围内，依据该可行装药方案是否为最终装药方案而定。式（7）为炮孔间装药结构互斥性约束，即各炮孔的可能方案只有其一为最终装药结构方案。式（8）为总装药量与装药单耗匹配约束，即最终装药结构的各炮孔总装药长度乘以装药线密度等于爆破范围体积乘以炸药单耗。

3 研发与应用

3.1 研发背景

某地下矿山东采区100中段130分段矿块顶板岩性为矽卡岩和灰岩，矿块底板岩性为矽卡岩和砂岩。岩性完整性一般，底板岩性质量高于顶板。矿块内存在局部断层裂隙，包含滴水和断层填充物。受断层破坏的影响，断层附近岩性较为破碎。矿块地质储量为18.26万t，矿石品位TFe为43.22%，MFe为38.01%。

该采场采矿方法为分段凿岩阶段落矿空场采矿法。设计在115 m分段布置底部结构，各分段爆下矿石在底部结构出矿。每隔2 m设计一炮排排位，共计 28排。按照目前CAD手工装药设计模式，时间在4 h以上，作业效率低，炮孔装药过程繁琐。

3.2 工程应用

以该矿山东采区100中段130分段2-5#采场为例，基于数字采矿软件平台DIMINE软件开发，实现了地下矿扇形中深孔装药设计工程应用。东采区2-5#采场地质资源及井下开拓三维模型如图2所示。以该地下矿山扇形中深孔爆破布孔设计某排布孔成果为例，如图3所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

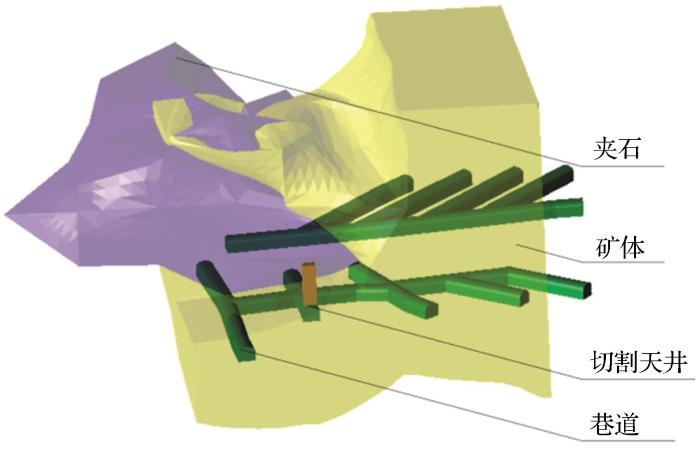
图2 东采区100中段地质及井下开拓三维模型

Fig.2 3D model of geology and underground development in 100 middle section of east mining area

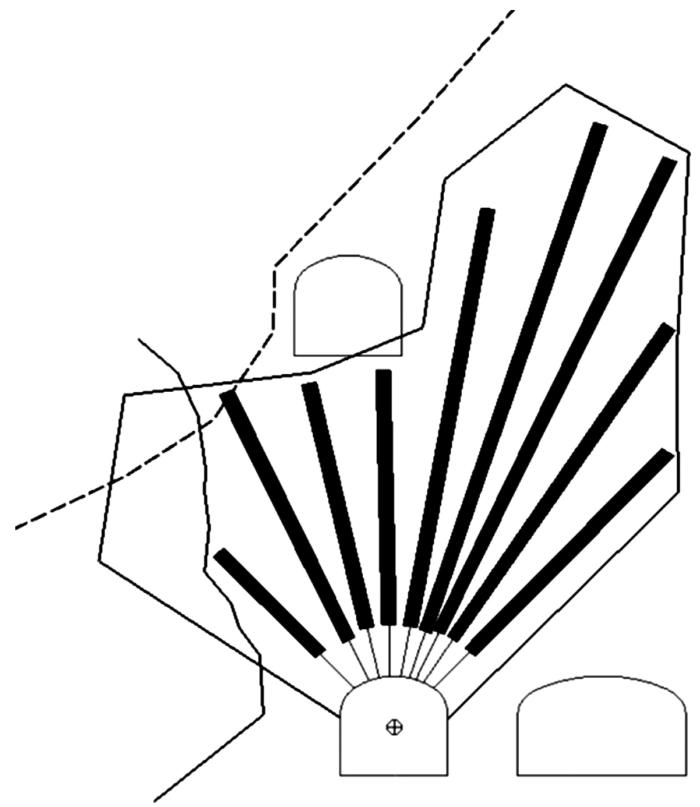
图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 某地下矿山扇形中深孔爆破布孔设计成果

Fig.3 Design results of fan-shaped medium-deep holes blasting hole arrangement in an underground mine

图3显示该排布置有1#~9#炮孔，并展示了矿岩分界面、采空区分边界、爆破边界和机芯点等布孔参考要素。根据矿岩分界面、采空区边界、爆破边界、巷道边界和机芯点位置的空间分布情况，首先提取所有矿岩分界面、采空区边界、爆破边界和巷道边界构成的最小闭环，如图4所示。图4中粗实线标记显示了利用矿岩分界面、采空区边界、爆破边界和巷道边界构成的8个最小闭环。以2#孔为例，选择该炮孔中点所在的最小闭环为爆破范围，如图4（f）所示。按离散化网格尺寸对爆破范围进行离散化，爆破范围离散化后的效果如图5所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 最小闭环及爆破范围

Fig.4 Minimum closed loop and blasting range

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 爆破范围离散化

Fig.5 Discretization of blasting ranges

图5显示该炮排的爆破范围被离散化为0.1 m×0.1 m的正方形网格。以2#炮孔 $h_{2}$ 为例，构建装药结构与担负矿量关系，即离散化网格的质心与炮孔 $h_{2}$ 装药结构的最小距离小于1.0 m的离散化网格的集合，如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 装药结构与担负矿量关系

Fig.6 Relationship between the charge structure and the quantity of ore carried

建立地下矿山炮孔装药结构优化设计数学模型并求解。通过现场爆破试验及装药设计精度要求，确定此次爆破范围装药参数包括：最小填塞长度为1.0 m，装药影响半径为1.0 m，排间距为2.0 m，爆破范围面积为270.61 m²，装药线密度为4.8 kg/m，孔径为80 mm，炸药单耗为0.86 kg/m³，离散化网格尺寸为0.1 m×0.1 m。将上述参数代入第2.1小节模型中，得到本次参数化装药的数学模型。

对各炮孔进行数学模型决策变量构建。以2#炮孔 $h_{2}$ 为例，如图7所示。图7将第2个炮孔 $h_{2}$ 的可行装药方案划分成y_2，1，y_2，2，y_2，3，…，y_2，12共12种。

图7

新窗口打开| 下载原图ZIP| 生成PPT

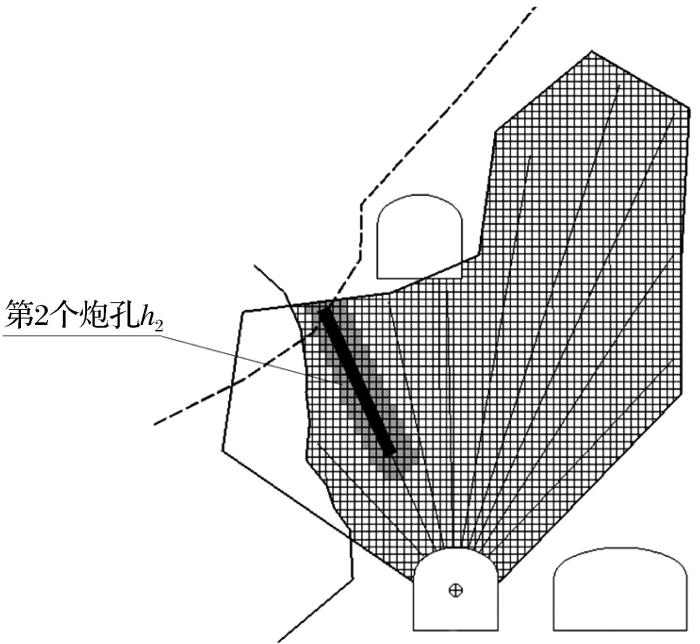
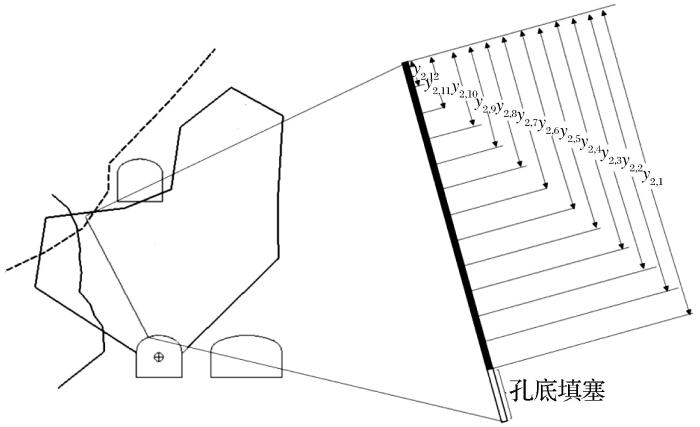
图7 装药设计决策变量构建示意图

construction for charge design

Fig.7 Schematic diagram of decision variables

结合式（1）~式（6）模型的约束条件及爆破范围最大化这一模型求解目标，采用运筹学方法对构建出的数学模型进行解算，计算结果为：y_1，1=1，y_2，5=1，y_3，1=1，y_4，4=1，y_5，1=1，y_6，8=1，y_7，3=1，y_8，6=1，y_9，1=1。以各炮孔对应装药方案绘制装药线，如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

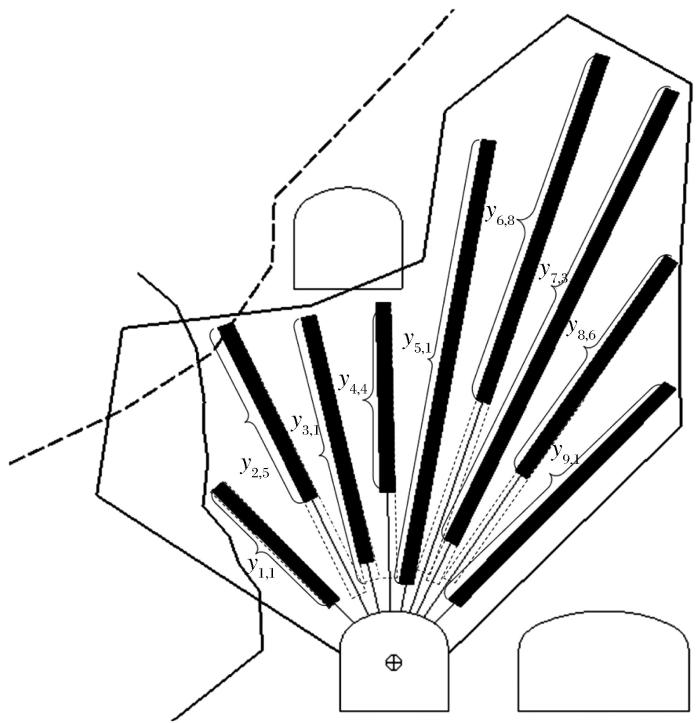
图8 扇形中深孔最终爆破装药求解结果

Fig.8 Solution results of final blasting charge of fan-shaped medium-deep holes

利用CAD人机交互设计出的爆破装药结构如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 人机交互装药设计结果

Fig.9 Results of human-machine interaction charge design

将图8和图9所示的2种装药设计进行对比，结果见表1。由表1可知，相比人机交互式装药设计，参数化装药设计考虑了单耗和装药影响半径等现场实际爆破参数。通过装药结构与担负矿量关系限制，输出的最终爆破装药方案确保了炸药担负矿量均匀性要求，更能满足现场实际爆破需求。

表1 2种方式装药设计结果对比

Table 1 Comparison of charge design results in two ways

炮孔编号	本文方法		人机交互式方法
炮孔编号	装药长度/m	填塞长度/m	装药长度/m	填塞长度/m
1#	5.71	1.00	4.91	1.6
2#	7.48	3.95	9.63	1.6
3#	8.98	1.74	8.92	1.6
4#	6.68	4.14	9.02	1.6
5#	15.86	1.00	15.06	1.6
6#	13.44	7.32	18.96	1.6
7#	18.25	2.42	18.87	1.6
8#	10.4	4.89	13.49	1.6
9#	10.78	1.00	9.98	1.6
总计	97.58	27.46	108.84	14.6

新窗口打开| 下载CSV

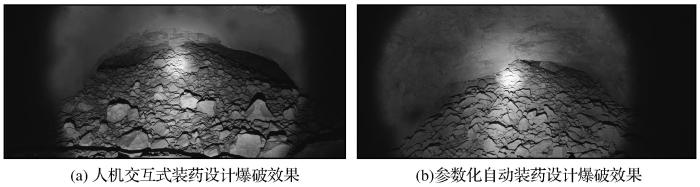
以相同地质及装药条件的2次爆破试验为例，爆破结果如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 2种装药设计方案爆破结果对比

Fig.10 Comparison of blasting effect of two charging design schemes

由图10可以看出，人机交互式装药设计下爆破试验的大块率明显高于参数化自动装药设计。为进一步分析爆破结果，利用相机对爆破后现场进行拍照，获取原始爆堆图形。对爆堆图像进行图像平滑和对比度调整等处理，提取照片中的矿块，并对照片中各矿块进行尺寸标定和统计分析。2种装药设计方案的块度分析如图11所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 2种装药设计方案块度分析对比

Fig.11 Comparison of block size analysis of two charge design schemes

根据现场矿石破碎要求，将块径500 mm以上的矿石认定为大块。图11所示的表面爆堆图像显示，采用参数化装药设计现场出矿大块率明显低于人机交互式装药设计。另外，采用参数化装药设计时间极大地缩短，从4 h减少至5 min。相比于人机交互式布孔需花费4 h，本文方法在有效改善爆破效果的同时，极大地提高了装药设计效率。

4 结语

（1）基于爆破范围离散化设计思想，构建了以装药量与担负矿量逻辑性约束、炮孔间装药结构互斥性约束及总装药量与装药单耗相匹配约束等为约束条件，以各项约束条件下装药结构的爆破影响范围最大为目标的地下矿扇形中深孔装药设计优化数学模型。

（2）将提出的地下矿扇形中深孔装药设计方法应用于某矿山。试验结果表明，相似地质条件和装药条件下2次爆破试验采用参数化装药设计时现场出矿大块率明显低于人机交互式装药设计，装药设计时间极大地缩短，从4 h减少至5 min。由此可见，地下矿扇形中深孔参数化装药设计方法最大程度地保障了炮孔间装药能量分布均匀性，保证了爆破质量，且装药设计时间大幅缩短，极大地降低了采矿设计技术人员工作量，提高了设计工作效率。

中国矿业报）

http://www.goldsci.ac.cn/article/2024/1005-2518/1005-2518-2024-32-6-1107.shtml

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[]

Cheng

Bing

， Wang

Haibo

， Zong

，et al，2023.

Mid-deep hole cutting blasting technology based on slit charge directional presplitting

［J］.Journal of Vibration and Shock，42（3）：322-329.

Gao

， Li

， Xiong

，et al，2023.

Refined design and optimization of underground medium and long hole blasting parameters—A case study of the Gaofeng mine

［J］. Mathematics，11：1612.

[本文引用: 1]

Himanshu

V K

， Roy

M P

， Shanker

，et al，2021.

Empirical approach based estimation of charge factor and dimensional parameters in underground blasting

［J］.Mining，Metallurgy and Exploration，38：1059-1069.

[本文引用: 1]

Liang

Rui

， Cao

Xiaorui

， Zhou

Wenhai

，et al，2024.

Effect of uncoupled charge coefficients on rock blast damage

［J］.Gold Science and Technology，32（2）：306-317.

Liu

Meng

，2017.

Design and application of parameters of medium and deep hole blasting in underground quarry

［J］. China Mining Engineering，46（4）：12-14.

Liu

Yichao

， Guo

Jinping

， Li

Jiaoqun

，et al，2021.

Optimization design of fan-shaped medium-deep hole blasting hole placement based on floyd algorithm

［J］. Blasting，38（1）：64-69，152.

Luo

Haohao

， Yang

Renshu

， Ma

Xinmin

，et al，2023.

Study on the distribution characteristics of deep hole blasting in the fan-shaped hole of Shilu iron mine

［J］.Journal of Mining and Safety Engineering，40（2）：371-378.

Wang

Chenglong

， Zhou

Xin

， Zhao

Xingdong

，et al，2021.

Application of downward fan-shaped medium and deep hole blasting in Sanshandao gold mine

［J］. Nonferrous Mining and Metallurgy，37（4）：18-21.

Wang

Huilin

， Zhang

Chengzhen

， Zhu

Minghai

，2012.

Three-dimensional blasting design for underground mines

［J］. China Mining Engineering，41（3）：5-7.

Wang

Ping

， Li

Bin

， Xu

Mengguo

，2015.

Research on the generation mechanism and control of large chunks of falling ore by fan-hole blasting

［J］. Blasting，32（2）：1-10，58.

Wang

Yang

， Fan

Caibing

， Li

Jiaoqun

，et al，2022.

Optimized design of blasting based on the correlation study of medium and deep hole blasting parameters in underground mines

［J］. Mining Technology，22（3）：154-157.

Xia

Hongbing

， Xu

Ying

， Zong

，et al，2008.

Research on parameters of deep hole blasting in deep large section hard rock tunneling

［J］. Metal Mining，38（1）：44-46.

Yang

Hengtao

，2017.

Research on the application of medium and deep hole blasting technology in underground iron ore mining

［J］.Inner Mongolia Coal Economy，（20）：120-121.

Yuan

Jieping

， Song

Jiadong

， Renze

，2008.

Research and pra-ctice of underground medium and deep hole large-scale bla-sting

［J］.Mining Research and Development，（1）：76-80.

Zhang

Gengcheng

， Wu

Fan

， Han

Rongcan

，et al，2021.

Development and application of intelligent design system for fan-shaped medium-deep hole blasting in underground mines

［J］. Modern Mining Industry，37（3）：153-156.

Zhang

Yuanjuan

， Wang

Gongzhong

， Wang

Xingrong

，et al，2013.

Numerical simulation analysis of blast damage range

［J］. Chemical Minerals and Processing，42（4）：31-33.

Zhao

Yanwei

， He

Dongmei

， Li

Xianglong

，et al，2014.

Research on block size control technology of medium-deep hole-fall blasting in underground mines

［J］. China Engineering Science，16（11）：48-52，57.

Zheng

Bingxu

， Feng

Chun

， Song

Jinquan

，et al，2015.

Numerical simulation study on the influence law of explosives unit consumption on the block size of hematite blasting

［J］. Blasting，32（3）：62-69.

Zhou

Keping

， Shi

Wenchao

， Wang

Mingzheng

，et al，2017.

Intelligent identification of large diameter deep hole blasting parameters to assist design

［J］. Blasting，34（4）：73-79.

Zhou

Yuan

，2019.

Improvement of the effect of medium and deep hole blasting in production

［J］. Rock Drilling Machinery Pneumatic Tools，（1）：60-62.

程兵，汪海波，宗琦，等，2023.

基于切缝装药定向预裂的中深孔掏槽爆破研究

［J］.振动与冲击，42（3）：322-329.

[本文引用: 1]

梁瑞，曹晓睿，周文海，等，2024.

不耦合装药系数对岩体爆破损伤的影响

［J］.黄金科学技术，32（2）：306-317.

[本文引用: 1]

刘猛

，2017.

地下采场中深孔爆破参数设计与应用

［J］. 中国矿山工程，46（4）：12-14.

[本文引用: 1]

刘益超，郭进平，李角群，等，2021.

基于floyd算法的扇形中深孔爆破布孔优化设计

［J］. 爆破，38（1）：64-69，152.

[本文引用: 1]

骆浩浩，杨仁树，马鑫民，等，2023.

石禄铁矿扇形中深孔爆破块度分布特征研究

［J］.采矿与安全工程学报，40（2）：371-378.

[本文引用: 1]

汪洋，范才兵，李角群，等，2022.

基于地下矿中深孔爆破参数相关性研究的爆破优化设计

［J］. 采矿技术，22（3）：154-157.

[本文引用: 1]

王成龙，周鑫，赵兴东，等，2021.

下向扇形中深孔爆破在三山岛金矿的应用

［J］. 有色矿冶，37（4）：18-21.

[本文引用: 1]

王辉林，张成珍，朱明海，2012.

地下矿山三维爆破设计

［J］. 中国矿山工程，41（3）：5-7.

[本文引用: 1]

王平，李斌，许梦国，2015.

扇形孔爆破落矿大块产生机理及控制研究

［J］. 爆破，32（2）：1-10，58.

[本文引用: 1]

夏红兵，徐颖，宗琦，等，2008.

深部大断面硬岩巷道掘进中深孔爆破参数研究

［J］. 金属矿山，38（1）：44-46.

[本文引用: 1]

杨恒涛

，2017.

中深孔爆破技术在井下铁矿开采中的应用研究

［J］. 内蒙古煤炭经济，（20）：120-121.

[本文引用: 1]

袁节平，宋嘉栋，欧任泽，2008.

地下中深孔大规模爆破的研究与实践

［J］. 矿业研究与开发，（1）：76-80.

[本文引用: 1]

张耿城，吴凡，韩荣灿，等，2021.

地下矿扇形中深孔爆破智能设计系统的开发与应用

［J］. 现代矿业， 37（3）：153-156.

[本文引用: 1]

张袁娟，王公忠，王幸荣，等，2013.

爆破损伤范围数值模拟分析

［J］. 化工矿物与加工，42（4）：31-33.

[本文引用: 1]

赵艳伟，何冬梅，李祥龙，等，2014.

地下矿山中深孔落矿爆破块度控制技术研究

［J］. 中国工程科学，16（11）：48-52，57.

[本文引用: 1]

郑炳旭，冯春，宋锦泉，等，2015.

炸药单耗对赤铁矿爆破块度的影响规律数值模拟研究

［J］. 爆破，32（3）：62-69.

[本文引用: 1]

周科平，史文超，王明政，等，2017.

大直径深孔爆破参数智能识别辅助设计

［J］. 爆破，34（4）：73-79.

[本文引用: 1]

周源

，2019.

中深孔爆破在生产中效果的改善

［J］. 凿岩机械气动工具，（1）：60-62.

[本文引用: 1]

Mid-deep hole cutting blasting technology based on slit charge directional presplitting

2023

Refined design and optimization of underground medium and long hole blasting parameters—A case study of the Gaofeng mine

2023

... 鉴于此，国内外学者对地下矿扇形中深孔装药设计方法进行了广泛而深入的研究.在经验公式优化领域，学者们深入探讨了地下采场环形爆破载荷的间距问题，通过优化钻孔和爆破参数，为地下矿山的爆破作业提供科学依据（Himanshu et al.，2021）.在CAD辅助工具应用方面，部分学者利用Visual Lisp等工具对CAD软件进行二次功能开发扩展，实现了扇形中深孔装药设计的自动化和高效化（周科平等，2017；刘益超等，2021）.在数值模拟分析方面，结合现场爆破试验和LS-DYN等数值模拟软件，对扇形中深孔爆破参数进行设计和优化，有效提升了爆破作业的安全性（Gao et al.，2023）.此外，在智能算法的探索中，利用改进极限学习机（ELM）和BP神经网络等算法，构建爆破设计模型，实现了爆破参数的智能化设定和装药优化调整（张耿城等，2021）. ...

Empirical approach based estimation of charge factor and dimensional parameters in underground blasting

2021

Effect of uncoupled charge coefficients on rock blast damage

2024

Design and application of parameters of medium and deep hole blasting in underground quarry

2017

Optimization design of fan-shaped medium-deep hole blasting hole placement based on floyd algorithm

2021

Study on the distribution characteristics of deep hole blasting in the fan-shaped hole of Shilu iron mine

2023

Application of downward fan-shaped medium and deep hole blasting in Sanshandao gold mine

2021

Three-dimensional blasting design for underground mines

2012

Research on the generation mechanism and control of large chunks of falling ore by fan-hole blasting

2015

Optimized design of blasting based on the correlation study of medium and deep hole blasting parameters in underground mines

2022

Research on parameters of deep hole blasting in deep large section hard rock tunneling

2008

Research on the application of medium and deep hole blasting technology in underground iron ore mining

2017

Research and pra-ctice of underground medium and deep hole large-scale bla-sting

2008

Development and application of intelligent design system for fan-shaped medium-deep hole blasting in underground mines

2021

Numerical simulation analysis of blast damage range

2013

Research on block size control technology of medium-deep hole-fall blasting in underground mines

2014

Numerical simulation study on the influence law of explosives unit consumption on the block size of hematite blasting

2015

Intelligent identification of large diameter deep hole blasting parameters to assist design

2017

Improvement of the effect of medium and deep hole blasting in production

2019

基于切缝装药定向预裂的中深孔掏槽爆破研究

2023

... 在金属矿山地下开采过程中，穿孔爆破作业是其重要环节（袁节平等，2008；王辉林等，2012；程兵等，2023）.中深孔爆破技术被广泛应用于地下矿山开采，合理设计其装药结构能够极大地提高矿山生产效率，并有效保障矿山爆破作业质量及生产安全（杨恒涛，2017；王成龙等，2021；汪洋等，2022；骆浩浩等，2023；梁瑞等，2024）.目前扇形中深孔爆破设计工作存在大量人工重复操作.在装药设计过程中，需要根据炮孔分布情况、爆破参数和地质条件变化反复调整（赵艳伟等，2014；王平等，2015；刘猛，2017；周源，2019）.大量重复性装药设计计算工作费时费力，且在设计过程中，人机交互式调整装药仅能满足基本的爆破装药设计参数要求，主观随意性较大. ...

不耦合装药系数对岩体爆破损伤的影响

2024

地下采场中深孔爆破参数设计与应用

2017

基于floyd算法的扇形中深孔爆破布孔优化设计

2021

石禄铁矿扇形中深孔爆破块度分布特征研究

2023

基于地下矿中深孔爆破参数相关性研究的爆破优化设计

2022

下向扇形中深孔爆破在三山岛金矿的应用

2021

地下矿山三维爆破设计

2012

扇形孔爆破落矿大块产生机理及控制研究

2015

深部大断面硬岩巷道掘进中深孔爆破参数研究

2008

... 首先，根据矿岩分界面、采空区边界、爆破边界、巷道边界和机芯点位置的空间分布情况，提取所有矿岩分界面、采空区边界、爆破边界和巷道边界构成的最小闭环（夏红兵等，2008）. ...

中深孔爆破技术在井下铁矿开采中的应用研究

2017

地下中深孔大规模爆破的研究与实践

2008

地下矿扇形中深孔爆破智能设计系统的开发与应用

2021

爆破损伤范围数值模拟分析

2013

... 最后，按离散化单元尺寸对爆破范围进行离散化，爆破范围内所有离散化网格定义为离散化集合（张袁娟等，2013；郑炳旭等，2015）. ...

地下矿山中深孔落矿爆破块度控制技术研究

2014

炸药单耗对赤铁矿爆破块度的影响规律数值模拟研究

2015

... 最后，按离散化单元尺寸对爆破范围进行离散化，爆破范围内所有离散化网格定义为离散化集合（张袁娟等，2013；郑炳旭等，2015）. ...

大直径深孔爆破参数智能识别辅助设计

2017

中深孔爆破在生产中效果的改善

2019

〈

〉