矿山采掘计划编制是矿山生产与经营过程中的一项重要工作。采掘计划编制是否科学合理,对资源综合利用、企业的经济效益和企业是否能够进行可持续生产等均有着重大影响(刘定一等,2018)。目前,国际学者在进行矿山生产计划优化时更多地考虑金属价格和运营成本不确定性(Zoran et al.,2019;Mokhtarian Asl et al.,2018)以及地质不确定性(Seyed-Omid et al.,2016;Kosztyán,2020)等因素。国内学者对于矿山生产计划的研究则主要是以运输成本最低、净现值最大和品位均衡等为目标(任助理等,2017;李瑞等,2017;顾清华等,2020a),采用的编制方法有计算机模拟法(蒋成荣等,2015)、数学规划法(顾晓薇等,2014)和计算机网络技术。
随着智能优化理论的不断发展,一些新方法被引入到矿山生产计划优化之中,比如遗传算法、粒子群算法和关键路径法等。刘定一等(2018)针对矿山采掘生产计划手工编制复杂、图表展示困难的问题,建立了地下矿多目标规划模型,并运用三维可视化技术进行展示;刘晓明等(2017)采用混合整数规划法来解决矿山采掘过程中的回采顺序优化问题;李国清等(2018)运用改进的遗传算法来求解地下矿生产接续与设备调度集成优化模型;马龙等(2018)运用改进的量子粒子群算法求解多金属矿山工业采掘生产计划模型;张林(2013)采用关键路径来求解最长生产路径。综上可知,目前关于矿山生产计划优化问题的研究侧重于通过调整回采顺序和工序衔接问题来提高矿山企业的经济效益,而针对最短工期问题的研究较少,其中,关键路径法无法解决资源约束问题。
关键链是由Goldratt(2009)提出的一种基于约束理论的项目管理方法,其核心思想在于识别并解决项目执行过程中的瓶颈问题,调控项目进度,降低生产成本。根据矿山采掘计划的特点,将关键链的思想运用于矿山采掘进度计划编制中,以资源约束下的最短工期为目标,建立了地下矿山采掘计划模型。因为矿山生产始终处于不确定和不断变化的动态过程中,采用人工查找的方法很难把握工程的关键链,所以本文提出了一种基于改进的深度优先搜索算法来自动查找资源约束下的关键路径,并通过实例验证算法效率和有效性,以期解决资源约束问题,缩短采掘计划的工期。
1 基本原理和流程
地下矿开采是指开凿一系列由地表进入矿体的巷道,对矿产资源进行回采的一种开采方式(黄俊歆等,2011)。地下矿开采有两大任务:一是掘进巷道;二是开采矿石。这2项任务合称采掘,它是地下矿山生产的中心工作。矿山根据地质条件采用不同的采矿方法,采矿工序也有差异,但采掘作业作为中心任务必不可少。本文以乌拉特后旗紫金矿业三贵口矿山的采掘计划编制为例,其计划编制涉及多种采矿方法,工序方面考虑掘进和采矿,采场开采按照先掘后采的顺序进行。
矿山采掘过程中存在多种资源约束(叶海旺等,2018),其中影响最大的资源是生产者(包括人员和生产设备,原则上一个操作人员对应一台设备)。在本文中,资源约束问题实质上就是要解决并行作业之间的生产者作业冲突,即生产者资源充足时,作业可以并行执行,而生产者资源不足时则需要赋予不同场地的多种工序一个资源优先级。矿山采掘过程中每个场地执行的工序顺序是固定的,场地顺序则是不固定的。对于存在资源冲突的作业,不同的工序需要视具体情况安排。
关键路径上的作业所耗费的时间决定了整个计划工期的长度(赵爱丽,2013)。查找资源约束下作业的关键路径,其长度即为项目的最短完工时间。由于矿山采掘的特点,矿山采掘计划的网络图不同于传统的有向图(有向图根据给定的开始节点和终止节点查找路径),在查找关键路径的过程中没有固定的开始节点和终止节点,为此提出了一种改进的深度优先搜索的关键路径自动查找方法。
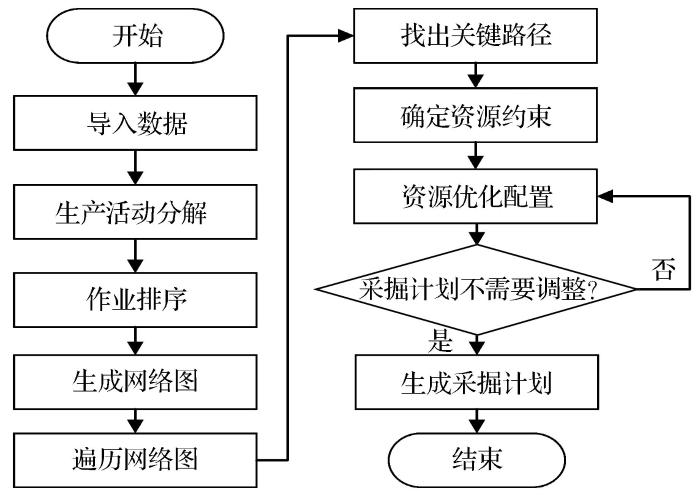
将矿山采掘计划与关键链结合起来,基于关键链的采掘计划编制的基本流程如图1所示。
图1
图1
基于关键链的采掘计划编制流程图
Fig.1
Flow chart of mining planning based on critical chain
步骤1:将整个矿山划分为多个中段,每个中段再根据实际需要划分为多个分段,每个分段再往下划分为多个采场,每个采场进行矿石开采需要经过若干道工序。本文中采场的工序为计划编制的基本单元,也称为一个作业(作业在网络图中表示为一个节点)。
步骤2:根据作业之间的逻辑衔接关系,对采掘作业进行排序,自动生成采掘计划网络图。
步骤3:为当前网络图中的作业添加资源约束,对于存在资源冲突的作业,建立资源冲突作业的优先级并更新网络图。
步骤4:采用改进的深度优先搜索遍历网络图,递归查找采掘路径,其中,耗时最长的路径即为关键路径。
步骤5:监督生产作业的执行进度,当实际进度和采掘计划出现偏差时,计算机能够根据一定的规则自动调整整个分段采掘作业之间的逻辑关系和资源配置,并根据调整的情况生成新计划。
2 算法的关键过程
2.1 定义
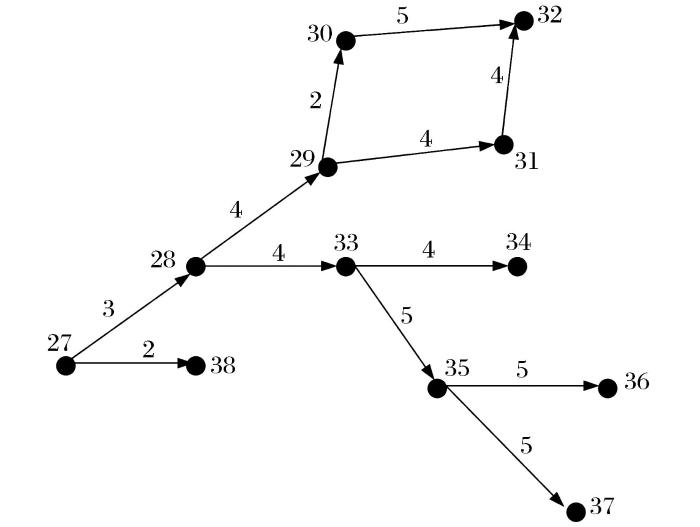
网络图是由作业(箭线)和事件(节点)组成的,用来表示工作流程的有向、有序的网络图形。网络图以图形的形式显示出项目中工作的发生顺序以及它们之间的逻辑关系。图中箭头表示作业,节点表示关系,每个作业包含2个节点,分别表示作业的开始时间和完成时间,箭线上的数字表示作业的持续时间(图2)。在网络图遍历过程中,每个节点只遍历一次,要对节点进行判断,需要进行记录和区分,为此引入了初始出度和可变出度的概念。其中,算法涉及的主要概念如下:
图2
紧前作业:是指紧接在当前作业之前的作业。紧前作业不结束,则当前作业不能开始。
紧后作业:是指紧接在当前作业之后的作业。当前作业不结束,紧后作业不能开始。
入度:以某顶点为弧头,终止于该顶点的弧的数目称为该顶点的入度。
出度:以某顶点为弧尾,起始于该顶点的弧的数目称为该顶点的出度。
开始节点:入度为0的节点。
终止节点:出度为0的节点。
初始出度:某顶点的初始出度值为其出度值,且在寻找关键路径的过程中该值不发生变化。
可变出度:某顶点的可变出度值为其出度值,但在寻找关键路径的过程中,该顶点每遍历一次可变出度值即减1。矿山采场有其特殊的命名方式,为方便表述,在网络图中用Id字段表示(采场Id具有唯一性)。如图2所示,27节点的入度为0,初始出度为2,为开始节点;32、34、36、37和38节点的初始出度为0,为终止节点;27和28节点之间的作业持续时间为3天。
图形有2种存储方式:邻接矩阵和邻接表。邻接矩阵通常用于图形的边较多的情况,而矿山网络图的结构较为简单,运用邻接矩阵存储会浪费大量的存储空间,而邻接表可以有效节省存储空间。同时,采用链表实现邻接表相对复杂,故采用二维数组来存储。
2.2 资源冲突作业优先级规则
矿山采掘的工序顺序固定,而采场顺序不固定,故按照工序顺序,逐一确定同一工序在不同采场的优先级。首先识别开始时间最早的作业场地和工序,第一种工序采用分层序列法,按照满足最早完成时间后再满足资源需求强度的规则,建立此种工序在不同采场的优先序列;任意采场后续工序的开始需要建立在前一工序完成的基础上,其优先序列由前一工序完成时间的先后确定。按照优先级进行资源分配,直到该采场当前工序完成,释放其所占用的资源,分配给下一个采场。其算法步骤如下:
步骤1:从工序顺序集中取第一个工序,查找所有采场该工序的最早开始时间和资源需求强度,并以此为依据赋予采场优先级。
步骤2:根据前一工序的完成时间为当前工序分配资源优先级,直至工序集中所有的工序都完成读取。
步骤3:为某一工序进行资源分配时,需要判断其上一个工序是否完成,若否,则进入等待状态;若是,则转至步骤4。
步骤4:在开始时刻计算当前资源剩余量,判断当前资源是否满足需求,若否,将剩余资源分给当前采场;若是,为该采场分配所需资源,并重复该步骤。
图3
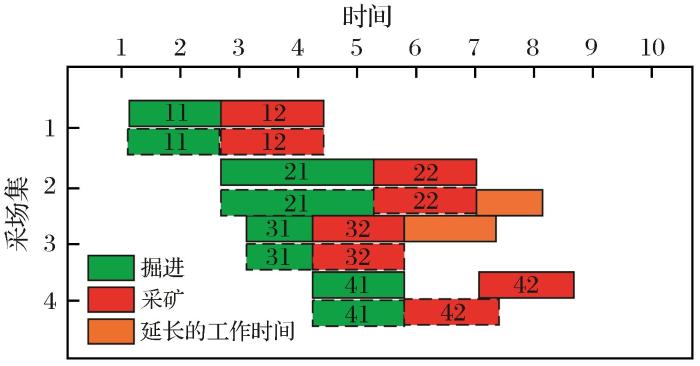
根据用户定义的计划衔接表(采场序号、工序序号、开始时间、结束时间、所需生产者资源和后继采场序号)生成甘特图。以图3为例(11表示第一个采场第一个工序),在ES(11)时刻,生产者资源满足11的需求,执行11,在EF(11)时刻当前采场进入下一工序,执行12;按优先级规则找到第一个工序的下一个采场,执行第一个工序21,在ES(31)时刻,生产者资源满足31的需求,执行31;在EF(31)时刻按掘进工序的优先级规则找到掘进的下一个采场,执行41,按采矿工序的优先级执行32;在ES(22)时刻,32尚未执行完,此时资源剩余量未能达到22的需求,仍将资源分配给22,但22的执行时间将会增加(即橙色部分);在EF(32)时刻,生产者资源满足42的需求,执行42。
因为生产者资源较一般的资源具有特殊性(顾清华等,2020b),即生产者数量不满足需求时也可以执行操作,为了避免产生生产者闲置的情况,提高设备利用率,在当前资源不足的情况下仍然将剩余资源分配给当前采场。
2.3 查找关键路径
搜索策略主要有广度优先搜索和深度优先搜索,其中,广度优先搜索是根据边来查找其邻接节点,深度优先搜索是根据节点来查找其邻接节点。2种搜索策略的效率与数据存储结构相关,且时间复杂度相当,区别在于遍历顺序不同。矿山采掘过程中每个采场执行的工序顺序是固定的,而采场顺序是不固定的,本文中查找的是不同工序的关键路径,查找下一个采场需要根据当前采场存储的工序信息和后继采场序号进行。因为本文主要是根据节点之间的逻辑衔接来查找其后继节点,故采用深度优先搜索的方法。
杜文文等(2020)采用改进的Dijkstra算法来查找2个节点之间的关键路径,然而矿山采掘过程中并没有明确的开始节点和终止节点,需要考虑多开始节点和终止节点的情况。针对不确定开始节点和终止节点的解决方案,同样也能解决确定下的开始节点和终止节点的关键路径查找问题。
因为存在开始节点和终止节点数量大于1的情况,为了便于操作,首先计算所有节点的出度和入度,入度为0的节点为开始节点,存储至开始节点集,出度为0的节点为终止节点,存储至终止节点集。
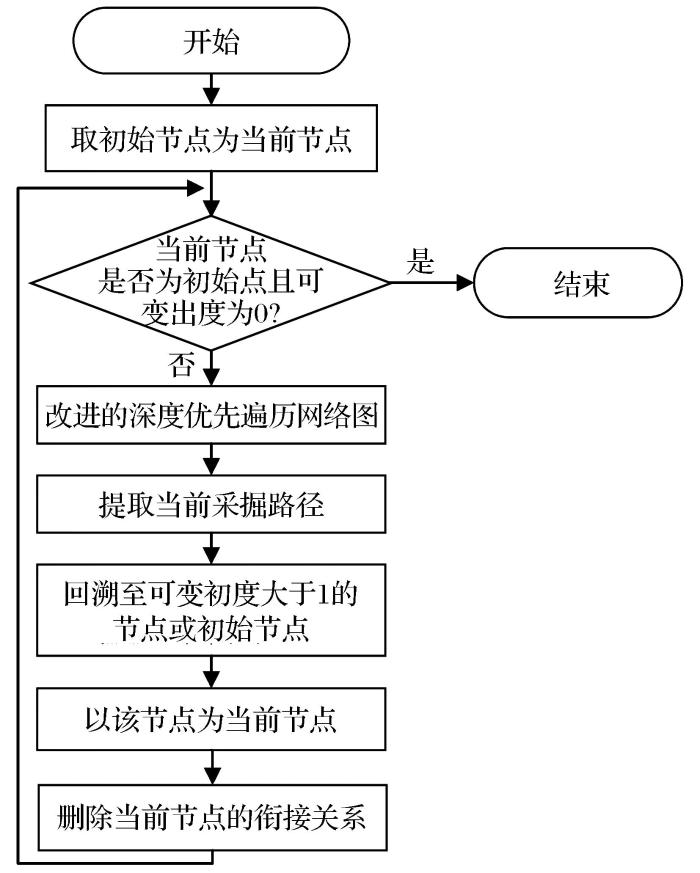
在网络图的遍历过程中,采用深度优先搜索算法查找某一节点关键路径的流程如下:
步骤1:从初始节点集中取一个未被遍历过的开始节点作为当节点。
步骤2:判断当前节点是否为开始节点且可变出度为0,若是,当前程序结束;若否,则转步骤3。
步骤3:运用改进的深度优先搜索算法遍历网络图,递归查找当前节点的后继节点,直至找到某一终止节点,代表着当前搜索完一条采掘路径。
步骤4:存储该路径及其采掘耗时至采掘路径集。
步骤5:回溯至可变出度大于1的节点或开始节点。
步骤6:以该节点为当前节点,删除当前节点与已遍历的后继节点的衔接关系,当前节点可变出度减1,转步骤2。
在查找完一个开始节点的所有采掘路径之后,比较且只保留该开始节点的最长路径,释放其他内存空间。最后对每个节点的最长路径进行比较,得到关键路径。这样既减少了比较次数,也减少了内存空间的占用,节省了时间和空间。查找关键路径的流程如图4所示。
图4
以图2的网络图为例,进一步说明深度优先搜索寻找关键路径的流程:
①从初始节点集中取一个初始节点27,以该节点为当前节点。
②对27节点进行判断,若结果为否,转步骤3。
③运用改进的深度优先搜索算法递归查找后继节点,直至找到其中一个叶子节点(以32节点为例),提取当前路径(27-28-29-30-32),将该路径及其采掘耗时14存入采掘路径集。
④回溯至可变出度大于1的节点29。
⑤以29为当前节点,删除29节点与30节点的衔接关系,转步骤2。
⑥遍历完路径27-38之后回溯至初始节点27,对27进行判断,27为开始节点,结果为是,程序结束。
2.4 采掘计划动态管理
采掘计划编制的最大特点是具有时间性(贾明涛等,2017),随着采掘作业的开展,实际执行情况和预期之间可能会出现偏差,确定出现偏差的作业是否为关键作业,若是,计算机能够根据上述规则自动调整资源优先级来调整关键路径,并根据调整后的情况优化出新的采掘计划。每次计划经过调整之后,计算机会对新计划进行重新计算,使得计划数据保持最新状态。
3 工程实例及对比分析
乌拉特后旗紫金矿业三贵口矿山位于内蒙古自治区巴彦淖尔市东升庙北3 km处,南距临河火车站52 km,矿山年产量为330万t。三贵口矿山属于地下开采矿山,主要的采矿方法有沿走向分段空场嗣后充填采矿法、垂直走向分段空场嗣后充填采矿法和浅孔留矿法。
2020年4月至2021年4月的年计划作业场地为530中段、580中段、630中段、680中段和730中段,完工期限为1年(按365 d计算)。采用关键路径法为该矿山编制采掘计划,以530中段为例,该中段共有17个采场,可用的掘进设备和采矿设备均为6台,采场之间的衔接关系和开始、结束时间及资源需求见计划衔接表(表1)。其中工序序号是表中的关键字段,工序序号为1表示当前工序为掘进,工序序号为2表示当前工序为采矿。
表1 三贵口矿山530中段采掘计划衔接表
Table 1
| 行号 | 采场序号 | 采场编号 | 工序序号 | 开始时间 | 结束时间 | 所需资源 | 后继采场序号 |
|---|---|---|---|---|---|---|---|
| 0 | 57 | 530-5203(9-3,9)KC | 1 | 2020/4/8 | 2020/4/14 | 3 | 58、59 |
| 2 | 2020/4/15 | 2020/4/18 | 3 | ||||
| 1 | 58 | 530-5202(9-3,9)KC | 1 | 2020/4/15 | 2020/4/21 | 3 | 60 |
| 2 | 2020/4/22 | 2020/4/27 | 2 | ||||
| 2 | 59 | 530-5204(9-3,9)KC | 1 | 2020/4/15 | 2020/4/21 | 2 | Null |
| 2 | 2020/4/22 | 2020/4/27 | 2 | ||||
| 3 | 60 | 530-5201(9-3,9)KC | 1 | 2020/4/22 | 2020/4/28 | 4 | 61 |
| 2 | 2020/4/29 | 2020/5/2 | 3 | ||||
| 4 | 61 | 530-5204(9)KC | 1 | 2020/4/22 | 2020/4/27 | 3 | 62 |
| 2 | 2020/4/28 | 2020/5/3 | 2 | ||||
| 5 | 62 | 530-5206(9)KC | 1 | 2020/4/28 | 2020/5/3 | 2 | 65 |
| 2 | 2020/5/4 | 2020/5/7 | 2 | ||||
| 6 | 63 | 530-5207(9)KC | 1 | 2020/4/8 | 2020/4/13 | 1 | 64 |
| 2 | 2020/4/14 | 2020/4/19 | 3 | ||||
| 7 | 64 | 530-5208(9)KC | 1 | 2020/4/14 | 2020/4/19 | 2 | 65 |
| 2 | 2020/4/20 | 2020/4/25 | 2 | ||||
| 8 | 65 | 530-5209(9)KC | 1 | 2020/5/4 | 2020/5/9 | 2 | 66 |
| 2 | 2020/5/10 | 2020/5/20 | 3 | ||||
| 9 | 66 | 530-5210(9)KC | 1 | 2020/5/10 | 2020/5/15 | 4 | 67 |
| 2 | 2020/5/16 | 2020/5/22 | 4 | ||||
| 10 | 67 | 530-5802(9-3,9)KC | 1 | 2020/5/16 | 2020/5/20 | 4 | Null |
| 2 | 2020/5/21 | 2020/5/29 | 2 | ||||
| 11 | 68 | 530-5803(9-3,9)KC | 1 | 2020/4/8 | 2020/4/19 | 2 | 69 |
| 2 | 2020/4/20 | 2020/4/26 | 2 | ||||
| 12 | 69 | 530-5803(9-3,9)KC | 1 | 2020/4/20 | 2020/5/3 | 2 | 70、71 |
| 2 | 2020/5/4 | 2020/5/9 | 4 | ||||
| 13 | 70 | 530-5804(9-3,9)KC | 1 | 2020/5/4 | 2020/5/12 | 2 | 72 |
| 2 | 2020/5/13 | 2020/5/22 | 2 | ||||
| 14 | 71 | 530-5805(9-3,9)KC | 1 | 2020/5/4 | 2020/5/11 | 3 | Null |
| 2 | 2020/5/12 | 2020/5/17 | 3 | ||||
| 15 | 72 | 530-6001(9)KC | 1 | 2020/5/23 | 2020/5/27 | 3 | 73 |
| 2 | 2020/5/28 | 2020/6/3 | 2 | ||||
| 16 | 73 | 530-6002(9)KC | 1 | 2020/5/29 | 2020/6/5 | 2 | Null |
| 2 | 2020/6/6 | 2020/6/10 | 1 |
根据表1可以自动生成三贵口矿山530中段的采掘计划甘特图如图5所示,其中,绿色表示掘进,红色表示采矿。图5(a)数据同表1,该甘特图中存在资源冲突,采用前面的资源分配优先级规则来解决该中段的资源冲突问题,得到优化后的甘特图如图5(b)所示。采用深度优先搜索方法对解决资源冲突之后的图进行遍历,查找掘进和采矿工序的关键路径。掘进工序关键路径上的采场序号分别为68、69、70、72和73,该中段原计划开采时间为2020年4月8日至2020年6月5日,现关键路径开采时间为2020年4月8日至2020年6月3日,节省了2 d时间。采矿工序关键路径上的采场序号为57、58、60、61、62、65、66和67,该中段原计划开采时间为2020年4月14日至2020年6月10日,现关键路径开采时间为2020年4月14日至2020年6月9日,节省了1 d时间,该中段实际作业时间与矿山原计划时间相比节省了1.67%。
图5
图5
三贵口矿山530中段采掘计划甘特图
Fig.5
Gantt chart for mining plan in 530 middle section of Sanguikou mine
运用传统手动编制法和关键路径法自动生成的计划完工时间分别为386 d和356 d,即关键路径法完工时间比传统手动编制法提前了30 d。其中,传统手动编制的计划比预期超出21 d,基于关键路径的采掘计划则比预期少了9 d,基于关键链的计划优化方法编制的计划最短工期相比传统手动编制有所缩短。原计划预估开采成本约为1亿5 400万元,运用关键链编制开采计划后开采成本比预期节省了178万元,可以满足矿山的年度开采规划。将本文中的方法与遗传算法(李国清等,2018)和关键路径法(张林,2013)进行对比分析。其中,运用关键路径法找到的关键路径与次长路径之间存在资源冲突,在优先为关键路径分配资源的情况下,导致了关键路径的变更,未能很好地优化工期。假设遗传算法种群大小为N,目标维数为M,迭代次数为Maxgen,标准化整个种群的时间复杂度为O(N),遗传算法的查找时间复杂度为O(N*M*Maxgen);关键路径法包括查找路径和比较路径2个部分,查找的时间复杂度由节点个数X和每个节点后继节点个数Y决定,表示为O(X*Y),设查找的路径数为L,每条路径依此进行比较,查找路径的时间复杂度为O(L2);关键链采取边查找边比较的方式,每条路径只需要比较一次,比较路径的时间复杂度为O(X*Y+L),因为节点个数远大于路径条数,故关键路径和关键链的时间复杂度都为O(X*Y)。由上述分析可知,遗传算法在初始化种群和迭代次数较大时,时间复杂度较高;关键路径和关键链的时间复杂度主要受节点数目的影响,相对较低。采掘计划编制方案对比分析结果见表2,可以看出基于关键链的方法在解决资源冲突和进行工期优化方面具有一定的优势。
表2 采掘计划编制方案对比分析
Table 2
| 指标 | 遗传算法 | 关键路径法 | 关键链 |
|---|---|---|---|
| 工期优化 | 1.2% | 0 | 1.67% |
| 成本 | - | - | 1% |
| 有解 | 非劣解 | 有解 | 最优解 |
| 解决资源冲突 | 是 | 否 | 是 |
| 时间复杂度 | O(N*M*Maxgen) | O(X*Y) | O(X*Y) |
当得到采掘计划的数据后,可以快速生成Excel表格、甘特图和柱状图等各类输出报表以及动画。其中,图表可以方便工作人员使用和编辑,为矿山管理人员提供决策依据,动画可以清晰明了地展示当前计划的执行进度,便于工作人员进行计划监督并对计划进行动态调整。矿山采掘计划编制的效果如图6所示。
图6
4 结论
(1)关键链可以清晰地反映出生产活动的进展情况,也可以通过对比实际执行情况和预期,优化调整得到新的采掘计划,提高了生产活动的按时完工率,降低了不确定性因素和突发状况带来的风险。
(2)运用关键链的思想对矿山企业短期采掘计划进行优化,可以解决并行情况下的资源冲突,相比传统计划编制方法,找出资源约束下的关键路径能够在相同的资源约束下缩短项目的工期,降低生产成本,为矿山进行科学、稳定的生产提供了新方法,该方法同样适用于其他作业的计划编制(如:中深孔计划编制)。
(3)本文提出了一种改进的深度优先搜索算法,该算法提高了内存空间的利用率,不足之处在于,该搜索方法是采用深度优先搜索所有路径,找出其关键路径,算法时间复杂度较高。
http://www.goldsci.ac.cn/article/2021/1005-2518/1005-2518-2021-29-4-602.shtml
参考文献
Research on route search based on improved Dijkstra algorithm
[J].
Modeling and algorithm of multi-objective production scheduling optimization for multi-metal open-pit mine
[J].
Long-term mining production scheduling model and optimization algorithm for open-pit mine enterprises
[J].
Improving optimization algorithm of production scheduling for open-pit metal mine
[J].
Dynamic optimization of production plans for multi-metal underground mines
[J].
A novel mining model for open-pit mine production scheduling
[J].
Application of aggregation staging algorithm in medium and long-term production planning of open pit
[J].
3D visualization production planning in underground mining based on simulating technology
[J].
An exact algorithm for the flexible multilevel project scheduling problem
[J].
Integrated optimization model for production and equipment dispatching in underground mines
[J].
Optimization model of mining operation scheduling for underground metal mines
[J].
A study on critical chain project network scheduling technology under double constraints
[J].
Optimization of mining operation plan based on multi-objective 0-1 programming
[J].
Study on multi objective optimization and application of medium and long term plan for underground mine
[J].
Production scheduling in underground mining using mixed interger programming
[J].
Mining production scheduling model and optimization algorithm for multi-metal mine industry
[J].
Integration of commodity price uncertainty in long-term open pit mine production planning by using an imperialist competitive algorithm
[J].
Optimization of drawing scheduling based on mixed integer programming in block cave mining
[J].
Integrating geological uncertainty in long-term open pit mine production planning by ant colony optimization
[J].
Multi-objective genetic particle swarm optimization algorithm for the short-term production planning in a mine
[J].
Application of key line method in the preparation of coal mining plan
[J].
Research on Production Schedule of Underground Mine Based on Key Chain
[D].
Long-term room and pillar mine production planning based on fuzzy 0-1 linear programing and multicriteria clustering algorithm with uncertainty
[J].
基于改进Dijkstra算法的进路搜索研究
[J].
多金属露天矿多目标生产计划优化问题建模及求解算法
[J].
露天矿山企业长期生产计划模型与优化算法
[J].
金属露天矿生产计划优化算法的改进
[J].
多金属地下矿山生产计划动态优化
[J].
一种新的用于编制露天矿生产计划开采模型
[J].
聚合分期算法在露天矿中长期生产计划编制中的应用
[J].
基于模拟开采技术的地下矿山三维可视化生产计划编制
[J].
地下矿山生产接续与设备调度集成优化模型
[J].
地下金属矿山采掘作业计划优化模型
[J].
双约束下关键链项目网络计划技术研究
[J].
基于多目标0-1规划的采掘作业计划优化
[J].
地下矿中长期计划多目标优化及应用研究
[J].
基于混合整数规划法的地下矿采掘计划编制
[J].
多金属矿山工业采掘生产计划模型与优化算法
[J].
基于混合整数规划法的自然崩落法放矿计划优化
[J].
矿山短期生产计划优化的多目标遗传粒子群算法
[J].
关键线路法在煤矿采掘计划编制中的应用
[J].
基于关键链的地下矿山生产进度计划研究
[D].







 甘公网安备 62010202000672号
甘公网安备 62010202000672号