Prediction of pipeline inner-corrosion based on principal component analysis and particle swarm optimization-support vector machine
0
2018
Research on using genetic algorithms to optimize Elman neural networks
1
2013
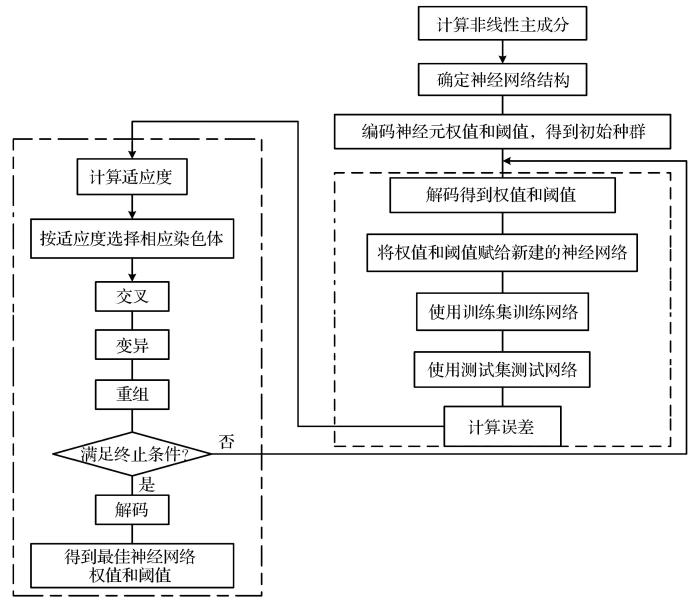
... 在将BP神经网络用于采场稳定性预测之前,应先确定最优的初始权值和阈值,然后使用遗传算法优化其权值和阈值(Lima et al.,2016;Ding et al.,2013),进而建立NPCA与GA-BP相结合的采场稳定性预测模型,以达到减少预测工作量和提高预测精度的目的.图1为所构建的NPCA-GA-BP神经网络模型流程图. ...
Grid search pptimised artificial neural network for open stope stability prediction
1
2021
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
Stability analysis and rock movement prediction of stope roof below the subsidence area
0
2015
Modeling of weld pool illumination based on GA optimizing BP neural network
0
2019
Stope roof stability prediction based on both SVM and grid-search method
0
2014
Study on stability evalution of layered deposit goaf based on BP neural network
0
2018
Differential evolution training algorithm for feed-forward neural networks
1
2003
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
Comprehensive evaluation of green super rice varieties based on nonlinear principal component analysis
0
2019
Application of VW-UM model in stope stability evaluation
0
2015
Forecasting method of expressway traffic volume based on NPCA and GA-RBF
0
2018
FLAC3D numerical simulation of open-pit transformation to underground slope and stability
0
2021
Prediction of stope roof displacement based on CT-GRNN
0
2015
Optimization of neural networks through grammatical evolution and a genetic algorithm
1
2016
... 在将BP神经网络用于采场稳定性预测之前,应先确定最优的初始权值和阈值,然后使用遗传算法优化其权值和阈值(Lima et al.,2016;Ding et al.,2013),进而建立NPCA与GA-BP相结合的采场稳定性预测模型,以达到减少预测工作量和提高预测精度的目的.图1为所构建的NPCA-GA-BP神经网络模型流程图. ...
Dynamic engineering classification of stope roof stability
0
2003
Study on stability evaluation and treatment scheme of goaf in Huanggang iron mine
0
2019
Evaluation of stope stability in underground mine;Hermyingyi(Sn-W deposit)mine in Myanmar
1
2021
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
Mining field stability analysis based on FLAC3D and Monte Carlo method
0
2018
An adaptive hybrid genetic algorithm for pavement management
1
2019
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
KPCA-SVM model for predicting Karst collapse tendency level
0
2015
Visual prediction of gas diffusion concentration based on regression analysis and BP neural network
1
2019
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
Prediction of stope stability based on random forest
0
2018
Bending force prediction model in hot strip rolling based on artificial neural network optimize by genetic algorithm
0
2018
Study on classification of improved artificial bee colony algorithm to optimi-zation of BP neural network
0
2018
Optimization of bolting scheme based on combination of principal component analysis and BP neural network
0
2012
Stability evaluation of surrounding rock and parameter optimization of stope under complex stress disturbance
0
2018
Optimization of filling slurry ratio in a mine based on back-propagation neural network
0
2013
Prediction model of aluminum consumption with BP neural networks in IF steel production
0
2017
Prediction of dust concentration based on particle swarm optimization BP neural network
0
2018
Analyzing and controlling the stope stability from open-pit to underground mining in Qinglonggou gold mine
0
2020
基于主成分和粒子群优化支持向量机的管道内腐蚀
1
2018
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
塌陷区下部采场顶板稳定性分析及岩移预测
1
2015
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
基于GA优化BP神经网络的焊接熔池照度建模
1
2019
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
基于网格搜索—支持向量机的采场顶板稳定性预测
1
2014
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
基于BP神经网络的层状矿床采空区稳定性评价研究
1
2018
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
基于非线性主成分分析的绿色超级稻品种综合评价
1
2019
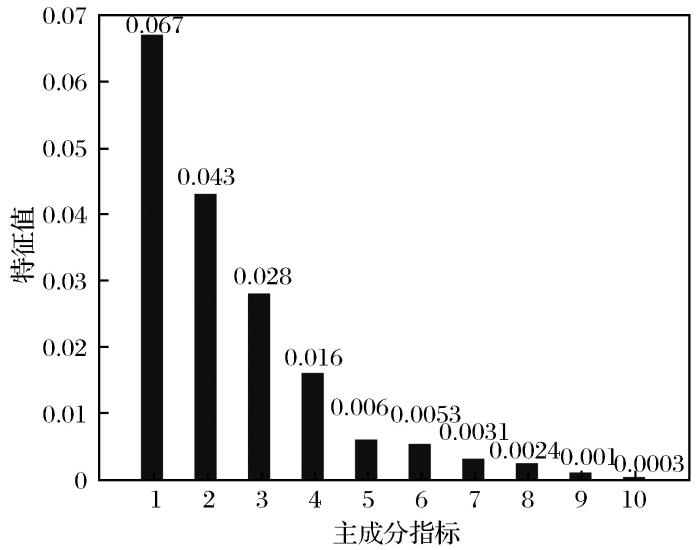
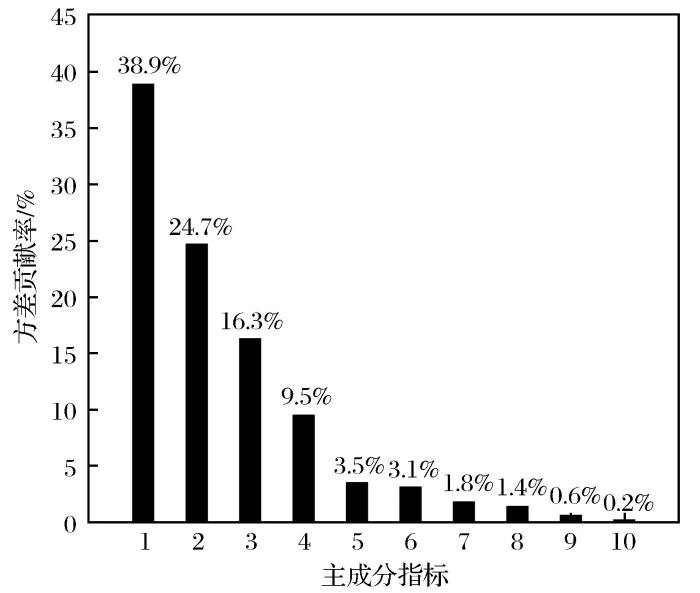
... 非线性主成分分析是主成分分析法的一种,主要解决的是非线性变量降维问题,其在一定程度上改进了传统主成分分析的线性化约束.通过分析变量与变量之间的相关性,利用非线性变换将包含重复信息的原始变量减少为维度更少的新变量,而这些新变量包含的信息可以近似等同于原有的信息.采用对数主成分分析法对原始数据进行非线性降维处理,因分析目的是降低维度,减少变量个数,故选取新变量的数目不会太多(一般不超过5个),保证新变量保留原始信息的80%即可(纪龙等,2019). ...
VW-UM模型在采场稳定性评价中得应用
1
2015
... 为验证本文方法的可靠性,选取凡口铅锌矿的33组实测数据(王杰等,2018),进行采场稳定性分析,样本数据见表1.在确定预测指标时,考虑尽可能全面客观地反映影响采场稳定性的主要因素,如岩石介质条件、采场结构特征和工程环境因素,同时指标易于测量或量化.根据这一原则,综合已有研究(康虞等,2015),选择10个影响因素为预测因子,其中采场深度(X2)、围岩抗压强度(X3)、岩体质量指标(X4)、节理间距(X5)、采场跨度(X7)、采场暴露面积(X8)和采场暴露时间(X9)为实测数据,采场地质构造(X1)、地下水影响(X6)和相邻采场开挖影响(X10)用半定量的方法取值,其量化值见表2,以采场稳定性(X11)为输出因子,将其划分为4类,1代表极稳定,2代表稳定,3代表不稳定,4代表极不稳定. ...
基于非线性主成分分析和GA-RBF的高速公路交通量预测方法
1
2018
... 式中:xij 为第i个数据的第j个指标的测量值(雷定猷等,2018). ...
FLAC3D数值模拟露天转地下边坡及采场稳定性研究
1
2021
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
基于CT-GRNN模型的采场顶板位移预测
1
2015
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
采场顶板稳定性动态工程分类
1
2003
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
黄岗铁矿采空区稳定性评价及治理方案研究
1
2019
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
基于FLAC3D和Monte Carlo法采场稳定性分析
1
2018
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
岩溶塌陷倾向性等级的KPCA-SVM预测模型
1
2015
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
基于随机森林理论的采场稳定性预测研究
3
2018
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
... 为验证本文方法的可靠性,选取凡口铅锌矿的33组实测数据(王杰等,2018),进行采场稳定性分析,样本数据见表1.在确定预测指标时,考虑尽可能全面客观地反映影响采场稳定性的主要因素,如岩石介质条件、采场结构特征和工程环境因素,同时指标易于测量或量化.根据这一原则,综合已有研究(康虞等,2015),选择10个影响因素为预测因子,其中采场深度(X2)、围岩抗压强度(X3)、岩体质量指标(X4)、节理间距(X5)、采场跨度(X7)、采场暴露面积(X8)和采场暴露时间(X9)为实测数据,采场地质构造(X1)、地下水影响(X6)和相邻采场开挖影响(X10)用半定量的方法取值,其量化值见表2,以采场稳定性(X11)为输出因子,将其划分为4类,1代表极稳定,2代表稳定,3代表不稳定,4代表极不稳定. ...
... 采场稳定性样本数据(王杰等,2018) ...
遗传算法优化神经网络的热轧带钢弯辊力预报模型
1
2018
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
改进人工蜂群优化BP神经网络的分类研究
1
2018
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
基于主成分分析与BP网络的锚杆支护方案优选
1
2012
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
复杂应力扰动下围岩稳定性评价与采场参数优化
1
2018
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
基于BP网络的某矿山充填料浆配比优化
1
2013
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
BP神经网络IF钢铝耗的预测模型
1
2017
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
粒子群算法优化BP神经网络的粉尘浓度预测
1
2018
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...
青龙沟金矿露天转地下采场稳定性分析及控制
1
2020
... 采场稳定性是矿山开采过程中不可忽视的动力灾害问题,其稳定与否直接关系到矿山生产是否安全,因此,科学准确地预测采场稳定性对矿山安全生产有着极为重要的现实意义.采场稳定性的分析预测方法较多,总体上可划分为2类:一类是基于力学理论的数学模型及数值模拟,如:Oo et al.(2021)、李启航等(2021)和乔守乐等(2018)运用FLAC3D对不同采矿方法条件下的采场稳定性进行了研究;龚剑等(2015)采用力学分析方法,建立岩移量时间序列来预测采场稳定性;赵兴东等(2020)、甯瑜琳等(2019)和张飞等(2018)等采用Mathews稳定图解法进行分析.另一类是应用机器学习模型,如:支持向量机模型(郭超等,2014;Zhou et al.,2012)、神经网络模型(李小贝等,2015;胡洪旺等,2018;Erten et al.,2021)和随机森林模型(王杰等,2018)等.其中,BP(Back Propagation,BP)神经网络具有处理复杂非线性系统的特点(张钦礼等,2013;张思源等,2017),有学者将其应用于采场稳定性预测领域(凌标灿等,2003).但BP神经网络在每次运算时是随机给定初始权值和阈值的,导致网络预测精度难以控制(王振华等,2018).因此,一些学者提出利用遗传算法(Genetic Algorithm,GA)(关子奇等,2019)、粒子群算法(赵广元等,2018)及改进人工蜂群算法(韦鹏宇等,2018)等进化算法对BP神经网络的初始权值和阈值进行全局寻优(Ilonen et al.,2003;Santos et al.,2019;Wang et al.,2019),大幅提高了网络预测精度.此外,采场稳定性受复杂的多指标影响(邵良杉等,2015),而各个指标之间会有重合的信息,若是将这些指标直接用于BP神经网络,预测效果不理想.为了减少指标之间的重合度,邬书良等(2012)和毕傲睿等(2018)提出利用主成分分析法对指标进行降维处理,再将得到的主成分指标用于神经网络预测. ...





 甘公网安备 62010202000672号
甘公网安备 62010202000672号