在参数标定研究中,学者们首先从宏微观参数的关系入手,通过模拟力学试验对其结果进行回归分析,分析各参数的敏感性以建立宏微观参数之间的经验公式。如:姜玥等(2023)通过单因素、响应曲面和回归分析法分析了宏细观参数的敏感性,并通过迭代法对其进行优化,简化了标定步骤;吴禄源等(2023)通过试错法对各微观参数影响程度进行排序,分析显著因子交互作用,建立了参数间的函数关系;冯豪天等(2022)通过直剪试验提出了一种用于胶结结构面参数的标定方法;赵国彦等(2012)通过理论研究定量地给出了宏细观参数的关系式;还有诸多学者进行了理论研究并给出函数式(阿比尔的等,2018;陈鹏宇等,2018;邓树新等,2019;黄宜胜等,2021;王朝阳等,2022)。这种借助参数敏感性标定微观参数的方式仍然受经验性的影响且可重复性较差,而构建函数关系式的方法对操作人员理论水平有一定的要求。
机器学习为参数标定提供了新的研究方法,颗粒流软件参数标定涉及多种微观参数和宏观参数,各参数间相互影响,具有很强的非线性特征。机器学习回归算法的本质是让计算机在数据中寻找规律,并进一步验证和修正规律,最后进行预测,将人工构建关系式的过程交给计算机,并通过测试数据进行调整。周小棚等(2020)通过反分析法建立BP神经网络模型反演出岩土体的细观力学参数;任俊卿等(2023)对标定模型进行轻量化分析,引入陡度因子和自适应动量项的改进BP算法实现对微观参数的标定;Benvenuti et al.(2016)提出了一种使用人工神经网络将宏观实验结果与微观数值参数进行关联的DEM仿真参数识别方法,能够准确且高效地预测不同输入参数的行为;钟惟亮等(2023)借助神经网络实现对地聚物混凝土的细观参数的标定工作;王洪波等(2022)使用BP神经网络完成对Burgers模型参数的标定。然而BP神经网络模型作为深度学习的基石,可以完成对复杂非线性模型的预测,但其需要足够数量的数据,通常上千组数据才能训练出准确的模型(吴昌友,2007)。
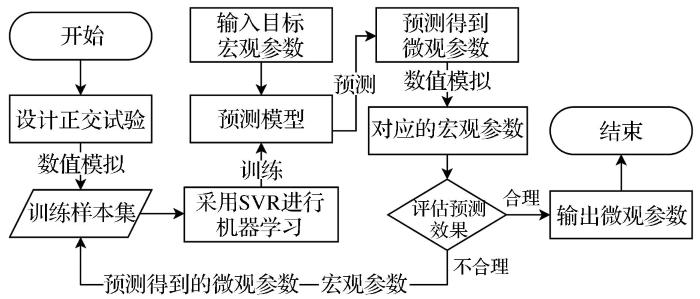
综上所述,通过函数搭建起宏微观参数关系式以及分析参数的敏感性来标定参数,仍然受经验性的影响且可重复性较差;而使用神经网络机器学习模型标定参数的准确率依赖于庞大的数据集。针对该问题,本文以平行黏结模型为例,通过正交试验构建小样本数据(数十组数据),以数值模拟为正演,机器学习预测为反演,即利用正反演结合的方法循环标定参数,标定流程如图1所示。不同于传统的机器学习预测模型,本文选择适合小样本数据的支持向量机模型(SVR),从较小样本数量出发,通过训练、预测和评估,动态增加数据集以逼近最终结果,这是一个逐渐构建数据库的过程,降低训练模型精度的影响,以更新数据集的次数评估其效率,不依赖训练样本的规模,可重复性强。
图1
1 PFC接触模型及微观参数
1.1 平行黏结模型
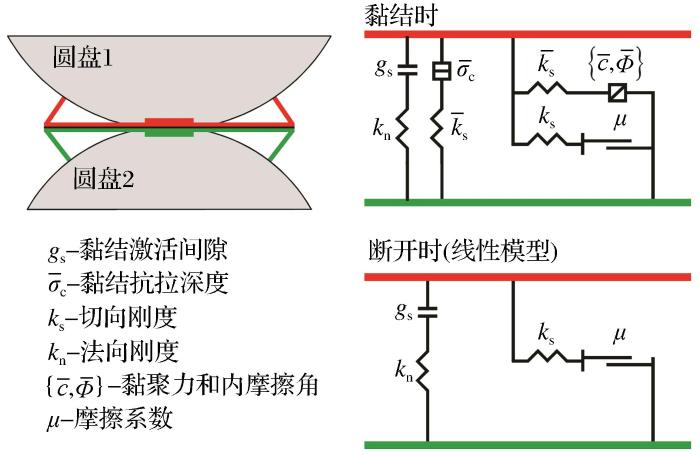
线性平行黏结模型(Linear Parallel Bond Model)常用来表征岩石材料的破坏过程,该模型描述了2个界面的行为:一个无限小的、线性弹性(不承受拉力)的摩擦界面来传递力;一个有限尺寸的、线性弹性的黏结界面来传递力和力矩,如图2所示。
图2
图2
线性平行黏结模型(Potyondy,2018)
Fig.2
Linear parallel bond model(Potyondy,2018)
使用线性平行黏结模型进行数值模拟时,需要分别标定平行黏结材料类参数和线性材料类参数。其中,平行黏结材料类包含线性组中有效模量(
这些参数累计14个,参考Potyondy et al.(2004)的研究,不同类组中3个有效模量、3个刚度比、2个摩擦系数可以设置为相同数值,
1.2 数值模型建立
考虑到计算效率,本文模拟使用PFC2D软件,通过单轴压缩试验标定岩石的弹性模量、泊松比和抗压强度,通过巴西劈裂试验标定岩石的抗拉强度。单轴压缩模型尺寸为50 mm×100 mm,加载板轴向应变率为0.025;巴西劈裂模型直径为50 mm,加载板轴向应变率为0.05。2个模型的最小颗粒直径为1 mm,最大颗粒直径为1.66 mm,材料密度为2 600 kg/m³,颗粒孔隙率为0.08,2个模型颗粒数分别约为3 250个和1 300个,模型如图3所示。
图3
1.3 正交试验
正交试验是研究多因素多水平的一种设计方法,该方法只挑选部分有代表性的点进行试验,可以有效降低研究时间和成本。本次正交试验的设计参考黄宜胜等(2021)关于砂岩参数标定的研究,在不考虑最小粒子半径影响的情况下,考虑砂岩的参数取值范围最终确定为6因素4水平,正交试验因素和水平数据见表1。
表1 正交试验因素和水平数据
Table 1
| 水平 | ||||||
|---|---|---|---|---|---|---|
| 1 | 3 | 1 | 0.2 | 15 | 15 | 15 |
| 2 | 6 | 2 | 0.4 | 30 | 20 | 30 |
| 3 | 9 | 3 | 0.6 | 45 | 25 | 45 |
| 4 | 12 | 4 | 0.8 | 60 | 30 | 60 |
根据上述试验因素和水平数据建立L32.4.6正交表进行数值模拟,获得与微观参数相对应的宏观参数,分别是弹性模量(
表2 正交试验表
Table 2
| 编号 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 1 | 0.2 | 15 | 15 | 15 | 4.82 | 0.169 | 22.40 | 5.47 | 4.1 |
| 2 | 3 | 1 | 0.4 | 45 | 30 | 45 | 4.94 | 0.146 | 52.67 | 11.85 | 4.4 |
| 3 | 3 | 2 | 0.2 | 45 | 25 | 60 | 4.10 | 0.305 | 42.37 | 5.92 | 7.2 |
| 4 | 3 | 2 | 0.4 | 15 | 20 | 30 | 4.23 | 0.268 | 27.57 | 5.28 | 5.2 |
| 5 | 3 | 3 | 0.6 | 60 | 15 | 30 | 3.85 | 0.324 | 36.57 | 7.61 | 4.8 |
| 6 | 3 | 3 | 0.8 | 30 | 30 | 60 | 4.00 | 0.313 | 35.51 | 7.79 | 4.6 |
| 7 | 3 | 4 | 0.6 | 60 | 25 | 45 | 3.63 | 0.399 | 43.90 | 7.62 | 5.8 |
| 8 | 3 | 4 | 0.8 | 60 | 20 | 15 | 3.69 | 0.384 | 52.92 | 10.90 | 4.9 |
| 9 | 6 | 1 | 0.6 | 60 | 20 | 45 | 9.33 | 0.143 | 35.84 | 5.66 | 6.3 |
| 10 | 6 | 1 | 0.8 | 30 | 25 | 15 | 9.48 | 0.128 | 38.53 | 6.78 | 5.7 |
| 11 | 6 | 2 | 0.6 | 30 | 30 | 30 | 7.76 | 0.271 | 41.94 | 8.26 | 5.1 |
| 12 | 6 | 2 | 0.8 | 60 | 15 | 60 | 7.90 | 0.250 | 23.96 | 3.86 | 6.2 |
| 13 | 6 | 3 | 0.2 | 15 | 20 | 60 | 6.47 | 0.381 | 18.64 | 3.48 | 5.4 |
| 14 | 6 | 3 | 0.4 | 45 | 25 | 30 | 6.82 | 0.366 | 48.67 | 9.92 | 4.9 |
| 15 | 6 | 4 | 0.2 | 45 | 30 | 15 | 6.01 | 0.438 | 52.30 | 10.76 | 4.9 |
| 16 | 6 | 4 | 0.4 | 15 | 15 | 45 | 6.28 | 0.404 | 19.93 | 3.61 | 5.5 |
| 17 | 9 | 1 | 0.2 | 60 | 25 | 30 | 12.38 | 0.173 | 37.31 | 5.99 | 6.2 |
| 18 | 9 | 1 | 0.4 | 30 | 20 | 60 | 12.89 | 0.149 | 24.73 | 4.72 | 5.2 |
| 19 | 9 | 2 | 0.2 | 30 | 15 | 45 | 10.51 | 0.305 | 21.80 | 4.93 | 4.4 |
| 20 | 9 | 2 | 0.4 | 60 | 30 | 15 | 10.93 | 0.275 | 47.84 | 11.88 | 4.0 |
| 21 | 9 | 3 | 0.6 | 15 | 25 | 15 | 10.15 | 0.338 | 16.06 | 3.61 | 4.5 |
| 22 | 9 | 3 | 0.8 | 45 | 20 | 45 | 10.20 | 0.336 | 32.68 | 6.74 | 4.9 |
| 23 | 9 | 4 | 0.6 | 45 | 15 | 60 | 9.35 | 0.381 | 21.76 | 3.36 | 6.5 |
| 24 | 9 | 4 | 0.8 | 15 | 30 | 30 | 9.01 | 0.378 | 18.62 | 3.55 | 5.3 |
| 25 | 12 | 1 | 0.6 | 15 | 30 | 60 | 16.00 | 0.152 | 19.95 | 5.62 | 3.6 |
| 26 | 12 | 1 | 0.8 | 45 | 15 | 30 | 16.38 | 0.133 | 26.66 | 4.66 | 5.7 |
| 27 | 12 | 2 | 0.6 | 45 | 20 | 15 | 13.77 | 0.252 | 34.41 | 4.83 | 7.1 |
| 28 | 12 | 2 | 0.8 | 15 | 25 | 45 | 14.17 | 0.243 | 20.61 | 3.77 | 5.5 |
| 29 | 12 | 3 | 0.2 | 60 | 30 | 45 | 11.38 | 0.364 | 47.45 | 9.02 | 5.3 |
| 30 | 12 | 3 | 0.4 | 30 | 15 | 15 | 11.92 | 0.313 | 24.45 | 4.70 | 5.2 |
| 31 | 12 | 4 | 0.2 | 30 | 20 | 30 | 10.42 | 0.421 | 27.92 | 5.23 | 5.3 |
| 32 | 12 | 4 | 0.4 | 60 | 25 | 60 | 10.99 | 0.410 | 31.41 | 5.02 | 6.3 |
由表2可知,根据微观参数模拟出的结果存在一点问题,即材料的单轴抗压强度约为抗拉强度的4~6倍,而通常二者之间相差一个数量级,这是由于平行黏结模型自身的局限性所导致的。根据蒋明镜等(2015)的描述,平行黏结模型是将颗粒之间的胶结关系简化为梁模型,该模型仅考虑胶结的抗拉和抗剪特性,能够单独模拟岩石材料的抗拉和单轴抗压破坏特性,但无法同时满足二者需求,即使如此,该模型仍是目前模拟岩石材料物理力学破坏特性的最有效且广泛使用的模型。
2 支持向量回归机参数设置
2.1 SVR模型
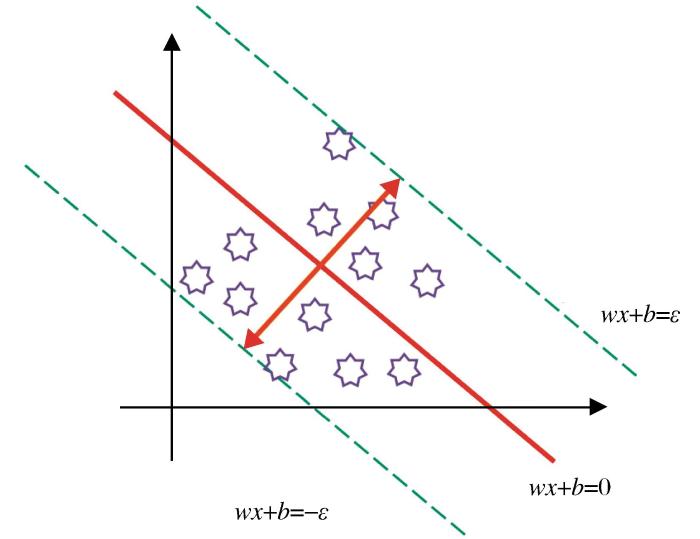
支持向量回归机(Support Vector Regression,SVR)是支持向量机(Support Vector Machines,SVM)的一种应用,是在统计学和机器学习中广泛使用的一种回归分析技术。与传统的回归分析模型寻求最小化预测值和实际值之间误差的平方和不同,SVR模型引进了不敏感损失函数(
图4
具体来说,SVR模型通过寻找一个函数[
2.2 SVR模型参数设置
在模型训练过程中,需要确定几个关键参数,即:核函数、容错参数
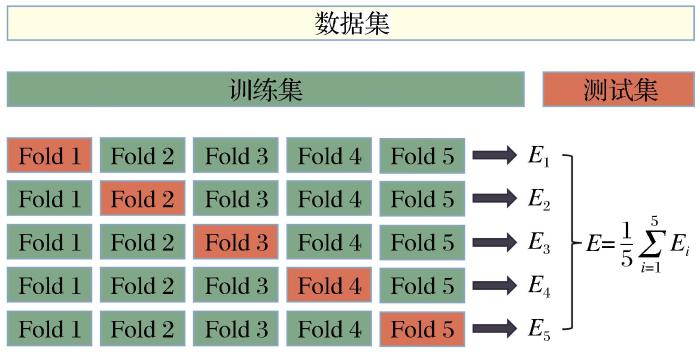
首先考虑到数据集较小,直接划分为训练集和测试集(通常按照8∶2划分),意味着无法充分利用所有数据,预测准确率依赖于模型数据量。本文采用K折交叉验证(K-Fold Cross Validation),其中K=5,K折交叉验证的过程涉及将原始数据集分割成K个大小相等的子集,通常称为“折”(folds)。K-fold交叉验证是一种用来优化超参数的常用方法,具体过程包括以下步骤:
(1)参数选择:首先为SVR模型选择一组超参数进行测试。本文选择优化的超参数为C、
(2)划分数据集:将数据集划分为K个大小相似的互斥子集(折)。随机分割,以确保子集的代表性和随机性。
(3)进行训练和验证:在每一轮中,选取一个子集作为测试集,其余的(K-1)个子集作为训练集。训练SVR模型,并记录模型在验证集上的性能。
(4)性能评估:重复上述过程K次,使用不同的折作为验证集,并计算其性能的平均值,分析平均均方误差(MSE),如图5所示。
图5
(5)选择最佳参数:在尝试多组超参数之后,选择使得模型在验证集上表现最佳的超参数组合。
(6)最终模型训练:使用选定的最佳参数组合对整个训练数据集重新训练SVR模型。
通常交叉验证是配合网格搜索对不同参数组合的性能进行评估,本文参数采用以下取值:
(1)C:在对数尺度上等比分布,C=[0.1,1,10,100,1 000];
(2)
(3)核函数:有4种核函数可供选择,分别是linear,rbf,poly,sigmoid。
2.3 SVR模型训练预测步骤
结合支持向量机模型的参数设置和K折交叉验证,整个模型训练预测步骤如下:
(1)导入数据集,转化为numpy数组,对数据进行标准化处理;
(2)设置SVR模型候选参数,参数如前文所述;
(3)训练模型,使用5折交叉验证,利用网格搜索(GridSearchCV函数)从SVR模型候选参数中寻找最优组合;
(4)预测,对输入的预测数据进行标准化、逆标准化处理。
3 基于SVR模型的微观参数辅助标定
表3 室内试验宏观参数
Table 3
| 编号 | ||||
|---|---|---|---|---|
| 1 | 8.40 | 0.290 | 29.8 | 2.4 |
| 2 | 8.87 | 0.221 | 26.2 | 2.4 |
| 3 | 16.71 | 0.270 | 47.3 | 9 |
3.1 第一组参数标定试验
表4 第一组参数标定结果
Table 4
| 次数 | 微观参数(预测) | 宏观参数(数值模拟) | 误差百分比/% | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6.52 | 1.73 | 0.516 | 25.3 | 15.7 | 41.4 | 8.66 | 0.248 | 27.4 | 5.6 | 4.9 | 3.1 | 14.5 | 8.1 | 132 |
| 2 | 7.04 | 2.27 | 0.478 | 28.5 | 19.1 | 42.1 | 8.64 | 0.285 | 30.1 | 5.9 | 5.1 | 2.9 | 1.7 | 1 | 144 |
| 待标定参数 | 8.40 | 0.290 | 29.8 | 2.4 | 12.4 | ||||||||||
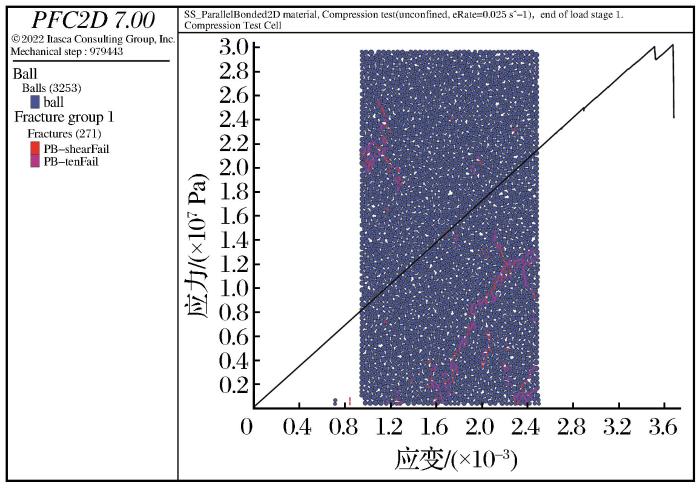
从第一组参数测试结果可知,当室内试验测得的抗拉强度不足单轴抗压强度的1/10时,预测参数模拟得到的抗拉强度和室内试验得到的抗拉强度差距较大(超过一倍),但模拟得到的压拉比约为5,这也验证了平行黏结模型的局限性,因此分析时忽略抗拉强度的误差。而弹性模量、泊松比和单轴抗压强度的预测效果较好,对于使用第1次预测出的微观参数进行模拟后所得到的宏观结果,除了泊松比外,其余2个参数误差均在10%以内。将该组参数加入数据集后重新预测,使用第2次预测出的微观参数进行模拟后所得到的宏观力学参数非常接近实验室测得的结果,第2次数值模拟应力—应变曲线如图6所示。
图6
图6
第一组预测参数PFC数值模拟结果
Fig.6
PFC numerical simulation results of the first set of prediction parameters
3.2 第二组参数标定试验
表5 第二组参数标定结果
Table 5
| 次数 | 微观参数(预测) | 宏观参数(数值模拟) | 误差百分比/% | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6.69 | 1.84 | 0.624 | 25.9 | 17.0 | 35.6 | 8.74 | 0.245 | 29.0 | 5.0 | 5.8 | 1.5 | 10.9 | 10.7 | 2.7 |
| 2 | 6.71 | 1.81 | 0.592 | 22.7 | 17.7 | 36.4 | 8.86 | 0.251 | 26.4 | 4.7 | 5.6 | 0.1 | 13.6 | 0.8 | 10.4 |
| 3 | 6.70 | 1.72 | 0.591 | 23.1 | 17.5 | 39.9 | 8.97 | 0.229 | 24.0 | 5.1 | 4.7 | 1.1 | 3.6 | 8.4 | 2.9 |
| 4 | 6.69 | 1.78 | 0.563 | 22.5 | 17.1 | 37.9 | 8.73 | 0.224 | 27.9 | 4.95 | 5.6 | 1.6 | 1.4 | 6.5 | 4.8 |
| 待标定参数 | 8.87 | 0.221 | 26.2 | 5.2 | 5.0 | ||||||||||
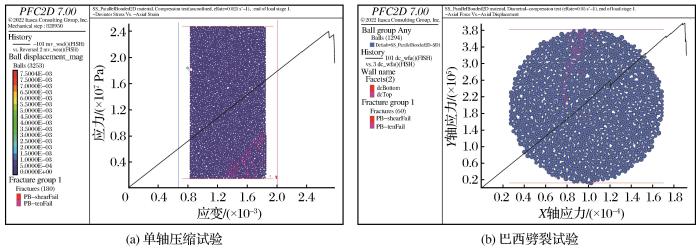
图7
图7
第二组预测参数PFC数值模拟结果
Fig.7
PFC numerical simulation results of the second set of prediction parameters
3.3 第三组参数标定试验
表6 第三组参数标定结果
Table 6
| 次数 | 微观参数(预测) | 宏观参数(数值模拟) | 误差百分比/% | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 12.6 | 2.11 | 0.526 | 57.1 | 24.3 | 31.8 | 14.4 | 0.272 | 43.4 | 8.0 | 5.4 | 13.8 | 0.7 | 8.2 | 10.1 |
| 2 | 13.0 | 2.26 | 0.503 | 59.4 | 26.4 | 32.0 | 14.4 | 0.285 | 46.5 | 10.1 | 4.6 | 13.8 | 5.6 | 1.7 | 11.1 |
| 3 | 13.5 | 2.25 | 0.480 | 56.2 | 27.9 | 27.0 | 15.3 | 0.290 | 49.3 | 9.8 | 5.0 | 8.4 | 7.4 | 4.2 | 9.1 |
| 4 | 14.2 | 2.14 | 0.495 | 61.9 | 26.5 | 30.5 | 15.9 | 0.279 | 50.3 | 9.2 | 5.5 | 4.8 | 3.3 | 6.3 | 2.3 |
| 待标定参数 | 16.7 | 0.270 | 47.3 | 9.0 | 5.3 | ||||||||||
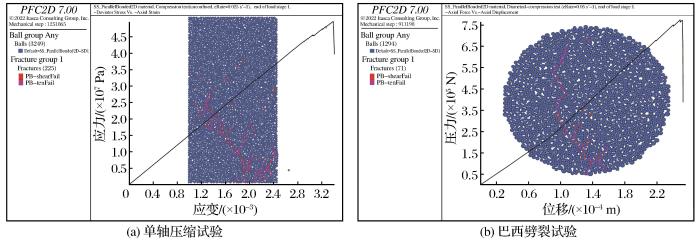
图8
图8
第三组预测参数PFC数值模拟结果
Fig.8
PFC numerical simulation results of the third set of prediction parameters
3.4 小结
借助支持向量回归机(SVR)模型对颗粒流微观参数进行预测,通过正反演结合的方法并利用小样本数据实现对微观参数的快速标定;对收集到的3组实验室测得的宏观参数进行预测,3组参数在3次以内的试算就完成对微观参数的标定,继续增加一次预测,以验证预测的合理性。此外,通过对样本数据和第一组标定结果的分析,再次验证了线性平行黏结的局限性,即无法同时较好地模拟岩石的单轴抗压强度和抗拉强度。
4 基于BP神经网络模型的微观参数辅助标定
利用BP神经网络标定微观参数是当前的研究热点。BP神经网络,即反向传播神经网络,利用前馈结构对数据执行映射,并通过后向传播算法迭代调整权重以最小化输出误差。这种网络能逼近复杂函数,广泛应用于分类和回归任务,其优点是适应性强,应用范围宽;劣势包括急剧依赖样本(通常需要上千组数据),容易陷入局部最优,深层网络中存在梯度消失问题,容易过拟合,且训练耗时较长。作为对比,本文测试BP神经网络模型正反演辅助标定在小样本中的表现。
4.1 BP神经网络模型参数设置
本研究中BP神经网络模型采用TensorFlow2框架,采用Adam优化器提高计算效率,因数据集较小不需要太多训练时间,学习率为Adam默认值0.001,模型由3层全连接层构成,包含2个隐藏层,每个隐藏层有5个神经元,激活函数为ReLU,输入输出层神经元数量由本文研究参数确定,分别为4个和6个。同样采用5折交叉验证分析平均均方误差(MSE),以评估模型。
4.2 BP神经网络模型微观参数标定
表7 BP神经网络参数标定结果
Table 7
| 次数 | 微观参数(预测) | 宏观参数(数值模拟) | 误差百分比/% | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8.03 | 2.26 | 0.511 | 36.5 | 21.6 | 38.5 | 9.62 | 0.302 | 38.1 | 8.7 | 4.4 | 8.5 | 36.7 | 45.4 | 66.5 |
| 2 | 6.46 | 1.47 | 0.553 | 41.5 | 18.5 | 49.6 | 8.14 | 0.218 | 33.0 | 5.6 | 5.9 | 3.0 | 1.4 | 26.0 | 6.5 |
| 3 | 6.24 | 1.86 | 0.660 | 41.1 | 19.3 | 53.6 | 8.43 | 0.253 | 34.4 | 6.2 | 5.6 | 5.0 | 14.5 | 31.3 | 19.6 |
| 4 | 6.12 | 1.50 | 0.532 | 41.0 | 20.3 | 56.9 | 8.51 | 0.216 | 31.5 | 5.8 | 5.4 | 4.0 | 0.5 | 20.2 | 11.1 |
| 5 | 6.82 | 1.92 | 0.659 | 44.6 | 16.6 | 59.6 | 9.15 | 0.256 | 26.8 | 4.5 | 6.0 | 3.2 | 15.8 | 2.3 | 13.5 |
| 6 | 6.81 | 1.67 | 0.602 | 41.0 | 18.9 | 52.4 | 9.21 | 0.229 | 30.5 | 5.8 | 5.3 | 3.8 | 3.6 | 16.4 | 11.9 |
| 7 | 5.85 | 1.63 | 0.581 | 42.6 | 16.6 | 55.5 | 8.11 | 0.225 | 27.0 | 4.8 | 5.6 | 8.6 | 1.8 | 3.1 | 6.9 |
| 8 | 6.35 | 1.62 | 0.637 | 46.5 | 18.0 | 55.9 | 8.61 | 0.216 | 27.7 | 5.0 | 5.5 | 5.7 | 2.9 | 2.3 | 4.6 |
| 待标定参数 | 8.87 | 0.221 | 26.2 | 5.2 | 5.0 | ||||||||||
由表7可知,对第7次预测得到的微观参数进行数值模拟,获得的宏观参数已达到预期,继续进行第8次预测,预测结果仍满足预期,认为应用BP神经网络模型可完成对PFC微观参数的标定,但标定效率不如SVR模型。以上结果符合2个模型的特点,即:SVR模型对样本的依赖相对较低,特别是在小样本或具有较高维度空间的数据上仍然可以比较好地工作,而BP神经网络通常需要大量数据来实现其强大的表征能力。
5 结论
以线性平行黏结本构模型为例,以提高微观参数标定效率为目的,基于正交试验以及PFC2D岩石单轴压缩试验和巴西劈裂试验建立小样本,通过机器学习完成微观参数的标定工作,得到以下结论:
(1)对于少量数据所组成的样本,通过机器学习直接预测出的微观参数很难达到预期,但是以机器学习预测为反演,数值模拟为正演,利用正反演结合的方法进行参数标定,可以有效提高微观参数标定效率。
(2)通过对比SVR模型和BP神经网络模型,SVR模型在处理小样本、非线性和高维度数据时更有优势,在微观参数的标定工作上效率更高。
(3)针对参数较多且具有较强的非线性特征的宏微观参数标定,通过机器学习的方法来辅助标定参数相较于人工试算更具优势,包括不受经验性影响,具有较强的可重复性,效率更高,推广性更强。
http://www.goldsci.ac.cn/article/2024/1005-2518/1005-2518-2024-32-4-675.shtml
参考文献
Relationship between particle micro and macro mechanical parameters of parallel-bond model
[J].
Identification of DEM simulation parameters by artificial neural networks and bulk experiments
[J].
Research on the calibration method of microparameters of a uniaxial compression PFC2D model for rock
[J].
A discrete numerical model for granular assembles
[J].
The Measurement and Analysis of Acceleration in Rock Slopes
[D].
Application of design of experiments in microscopic parameter calibration for hard rocks of PFC3D model
[J].
Study on calibration method of cemented structure plane parameters in numerical test
[J].
Study on genetic-neural network method of displacement back analysis
[J].
Calibration method of mesoscopic parameters for parallel bonding model of sandstone particle flow
[J].
Calibration of micro-parameters of parallel bonded model for rocks
[J].
A study on the correlation of macro and microstructural parameters of hollow cylindrical grey sandstone based on PFC
A bonded-particle model for rock
[J].
Lightweight analysis method for rock macro-meso parameters based on improved BP algorithm
[J].
Calibration method of mesoscopic parameters using BP neural network and Burgers model
[J].
A transversely isotropic rocks integrated microparameter calibration method for flat joint model and smooth joint model
[J].
The Research and Application on Nerual Network
[D].
Study on the correlation of macro and meso parameters of parallel bond model sandstone
[J].
Study of effects of microparameters on macroproperties for parallel bonded model
[J].
Research on mesoscopic parameters calibration of geopolymer concrete upon BP neural network
[J/OL].
Research on calibration method of discrete element mesoscopic parameters based on neural network landslide in Heifangtai,Gansu as an example
[J].
平行黏结模型宏细观力学参数相关性研究
[J].
岩石单轴压缩PFC2D模型细观参数标定研究
[J].
试验设计法在硬岩PFC3D模型细观参数标定中的应用
[J].
数值试验中胶结结构面参数标定方法的研究
[J].
位移反分析的进化神经网络方法研究
[J].
砂岩颗粒流平行黏结模型细观参数标定方法研究
[J].
基于PFC3D的空心圆柱灰砂岩宏细观参数相关性研究
[J/OL].
模拟岩石的平行黏结模型微观参数标定
[J].
基于改进BP算法的岩石宏细观参数轻量化分析方法
[J].
横观各向同性岩体平直—光滑节理双模型细观参数联合标定方法
[J].
采用BP神经网络和Burgers模型的细观参数标定
[J].
神经网络的研究及应用
[D].
砂岩颗粒流平行黏结模型宏细观参数关联性研究
[J].
平行黏结模型中细观参数对宏观特性影响研究
[J].
基于BP神经网络的地聚物混凝土细观参数标定研究
[J/OL].
基于神经网络的离散元细观参数标定方法研究——以甘肃黑方台黄土滑坡为例
[J].






 甘公网安备 62010202000672号
甘公网安备 62010202000672号