随着我国经济的快速发展，对公路交通运输的需求不断增长，为缓解日益拥堵的交通问题，四车道及以上的超大断面公路隧道的建设也逐渐增多（曲海锋，2009）。现有的公路隧道规范仅对双车道和三车道隧道的施工开挖方法和设计做出了明确规定，而四车道及以上的超大断面隧道的设计和施工尚缺乏规范的指导。

近年来，许多学者采用数值模拟、现场试验和理论分析等方法对超大断面结构隧道建设相关技术进行了研究，并取得一定的成果。断面的扁平率是影响隧道结构性能和经济效益的重要因素，目前已有多项研究采用数值模拟、现场调研和室内模型试验等方法对断面扁平率参数进行了优化设计，确定了隧道断面的最优扁平率（郭新新等，2019；黎略，2021；马连友，2021）。在施工工法方面，学者们通过对比双侧壁导坑法、小导洞先入法、中隔壁法和三台阶法等不同工法下的地表沉降、围岩变形、围岩塑性区范围和衬砌受力等指标，对各种工法的适用性和优劣性进行研究，进而确定最优施工工法（冉龙洲，2021；乔钢等，2022；梅宇等，2023；李合银等，2024），为工程实践提供了参考依据。在施工力学行为研究方面，现有研究主要采用理论分析、数值模拟以及统计分析与现场实测相结合的方法，对不同施工工法和不同支护参数下的围岩压力、围岩破坏演化特征等进行深入研究（屈慧森，2021；赵卫等，2020；刘道平，2021）。在施工参数方面，部分学者采用数值模拟方法对超大断面结构隧道的施工参数进行了优化分析（王小锁，2019；蔡东明，2021；林可夫等，2021；李相兵等，2022；王峰等，2024），给出了相应工程条件下的最优施工参数。

虽然针对隧道工程的研究已有较多成果，但在超大断面结构隧道的断面形状、施工工法和施工力学行为方面的研究仍有待深入（张俊儒等，2020），特别是针对超大断面隧道台阶法施工参数的相关研究较少。本文选择超大断面扁平结构公路隧道工程作为研究对象，建立数值模型，模拟其开挖及支护过程，利用数值模拟结果分析台阶法施工中不同台阶长度和不同锚杆间距对隧道围岩位移和稳定性的影响，通过优化现场施工参数，并结合现场监测结果验证数值模拟结构的准确性，在保证围岩稳定性的前提下达到提高施工效率和节约成本的目的。本文研究结果对相关隧道工程的设计和施工参数选取具有一定的指导意义和参考价值。

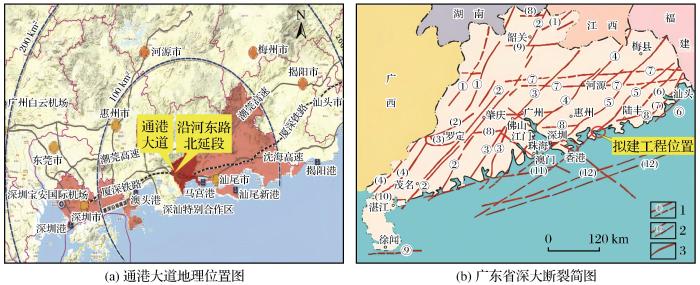
深汕合作区通港大道2#隧道位于广东省深汕特别合作区西南侧［图1（a）］，是穿越山岭的矿山法隧道，其中右线起讫里程桩号为YK6+739.708~ YK7+098.708，长约359 m，左线起讫里程桩号为ZK6+688~ZK7+089，长约401 m。隧道按照单洞四车道规模建设，开挖断面较大，单洞面积约为232m2，扁平比为0.615，属于超大断面扁平结构隧道（彭波，2021），隧道周边围岩二次应力分布较为复杂。此外，地勘报告显示隧道的围岩组成为Ⅲ~Ⅴ级围岩，区域地质构造比较复杂，以断裂为主，褶皱与断裂相伴而生，由于受到多次断裂作用及岩浆侵入破坏多数不完整，近场区存在断裂带［图1（b）］。综上，本工程隧道开挖工况相对复杂，增加了开挖过程中围岩不稳定的风险。

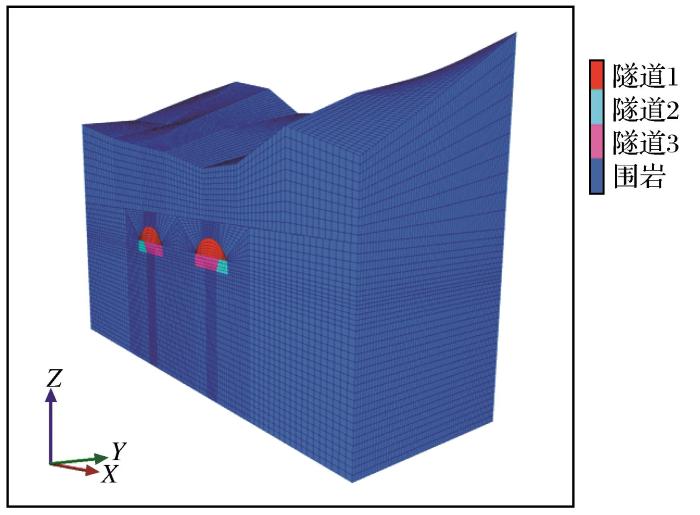
本文利用有限差分软件FLAC3D建立对数值模型，结合现有文献（林可夫等，2021；王峰等，2023）和以往研究经验，选择摩尔库伦本构模型进行建模，对通港大道2#隧道的Ⅲ级围岩段（左线里程桩号为ZK6+790~ZK6+850，右线里程桩号为YK6+810~YK6+870）的开挖和支护过程进行模拟，由于本隧道左、右洞长度不同，且起始桩号不同，因此左、右洞的桩号不匹配，二者在数值上有约20 m的差距。隧道地形平面图如图2（a）虚线框所示，图上方的隧道为左洞，图2（b）和图2（c）分别为左洞、右洞的隧道周围岩体剖面图。所建立的双线数值模型如图3所示，模型的宽度为178 m（X=178 m），沿隧道开挖方向模型的长度为60 m（Y=60 m），隧道开挖断面为三心圆，模型的顶部边界形貌根据实际工程中的山体特征建立［图2（a）虚线框］，模型的左右边界限制x方向的位移，模型前后边界限制y方向的位移，模型底部边界限制x、y、z方向的位移，数值模型中的材料参数见表1，地勘报告中显示隧道近场区存在断裂带，为了在数值模型中反映这种岩体特征，故选取的泊松比较大，黏聚力偏小。计算时首先根据模型的围岩自重应力计算收敛形成初始应力场，在进行隧道开挖前，将模型内部各单元x、y、z方向上的位移以及加速度设为0，使最终的模拟结果仅与开挖卸载和初期支护有关。根据本项目地勘资料，地下水位变化幅度较小，地下水相对稳定且与地表水联系较为紧密，地下水对隧道周边围岩影响较小，为简化计算，模型中不考虑地下水和节理裂隙等的影响。

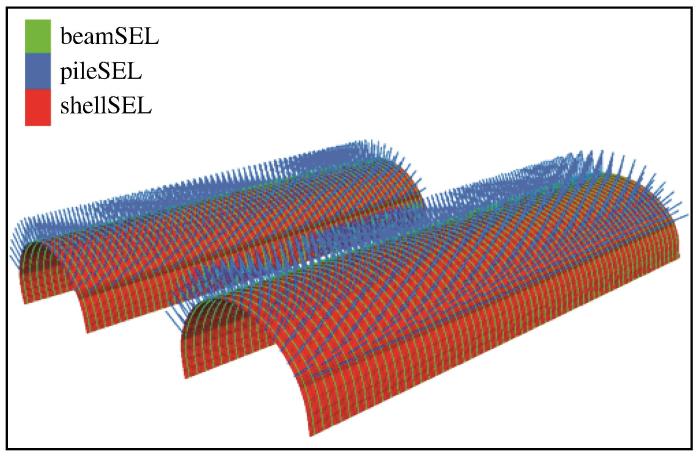
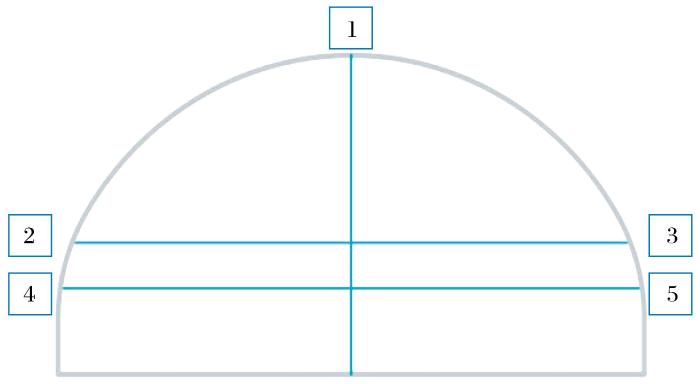
如图4所示，开挖过程中的支护工序即锚杆、钢拱架、喷射混凝土分别采用FLAC3D中的Pile单元、Beam单元和Shell单元进行构建（刘波等，2005），模型支护结构的材料参数如表2所示。在模型隧道轴线方向每隔10 m的开挖断面周边设置一组观测点，其设置位置如图5所示，各隧洞均有7个观测断面。模型中左洞的观测断面分别对应工程现场桩号ZK6+790、ZK6+800、ZK6+810、ZK6+820、ZK6+830、ZK6+840、ZK6+850，右洞的观测断面分别对应于桩号YK6+810、YK6+820、YK6+830、YK6+840、YK6+850、YK6+860、YK6+870。其中观测点1记录拱顶的竖向位移，测线2-3（观测点2、3连线）、测线4-5（观测点4、5连线）记录水平位移值。

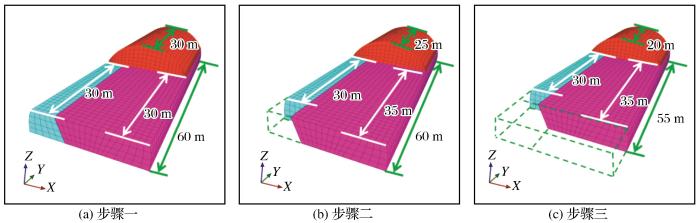
数值模型中的隧道开挖和支护过程与实际施工方案相同，即在隧道某部分开挖以后立即对该部分进行初期支护。根据现场实际施工方案，Ⅲ级围岩段现场施工每次进尺长度略有不同，但基本维持在5 m左右，因此在模型中设定开挖循环的进尺为5 m，在左洞整体断面掘进15 m后，再进行右洞的开挖。图6所示为左洞台阶长度为30 m时的开挖方案示意图（右洞的开挖方案与左洞的开挖方案镜像对称），主要的施工步骤如下：（1）上台阶开挖至台阶长度（图中为30 m）并完成开挖部分的初期支护；（2）上台阶与左下台阶开挖断面同步前进一个循环进尺（5 m）以及相应部分的初期支护；（3）上台阶、左下台阶和右下台阶同步前进一个循环进尺以及相应部分的初期支护。在开挖过程中，左下台阶（浅蓝色单元）与上台阶（红色单元）在上台阶开挖完成之前始终保持着一个台阶长度的距离，左下台阶（浅蓝色单元）与右下台阶（粉色单元）错开一个循环进尺的距离。

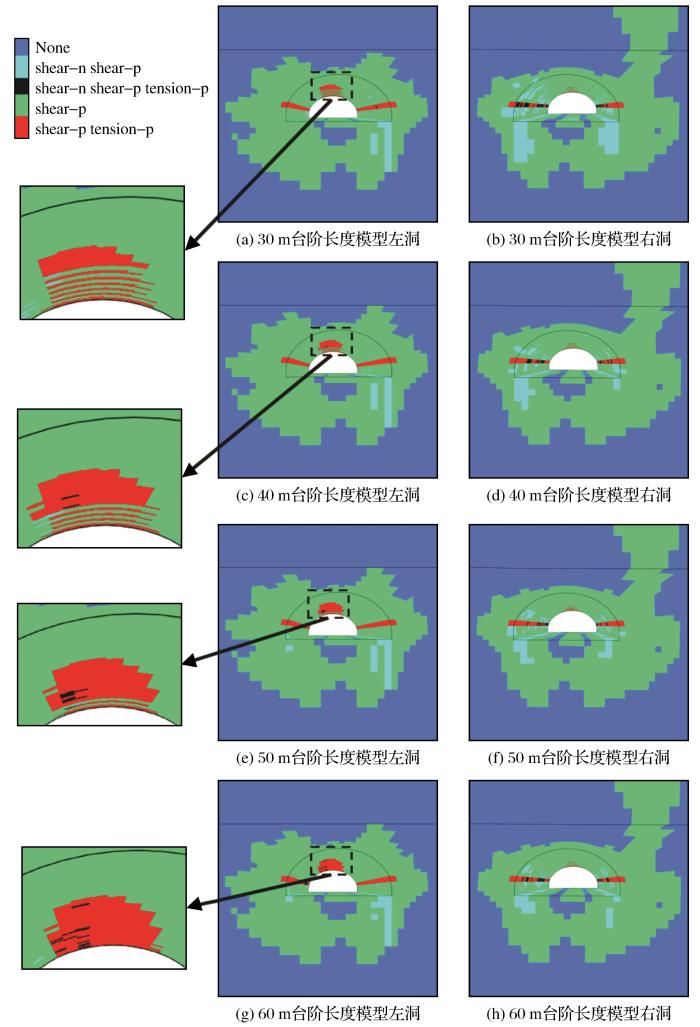
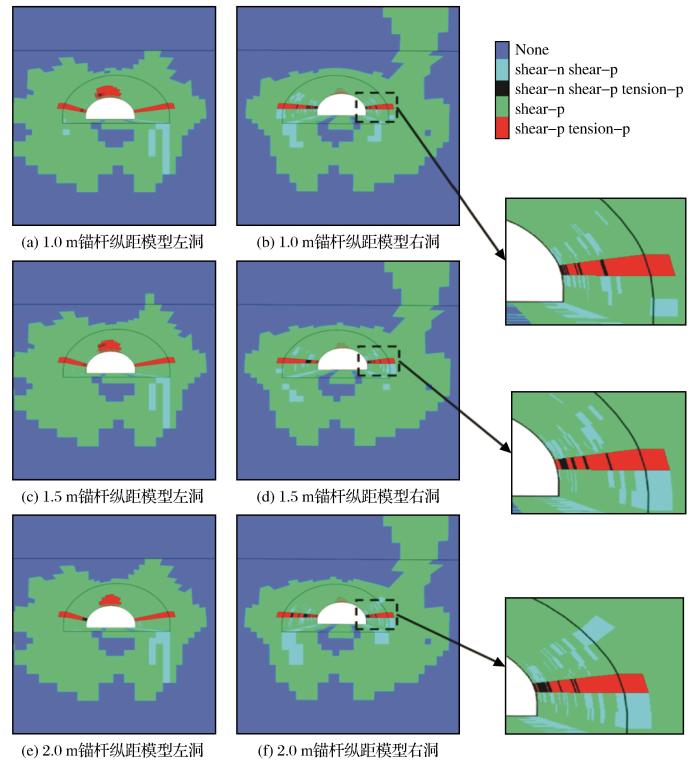
《公路隧道施工技术规范》（中交—公局集团有限公司，2020）中规定长台阶法适用于Ⅱ~Ⅲ级围岩三车道，短台阶法适用于Ⅲ~Ⅳ级围岩三车道，短台阶法的台阶长度为5~50 m，长台阶法的台阶长度大于50 m。根据规范和工程现场施工进度，利用所建立的数值模型对开挖过程中留设不同台阶长度的情况进行模拟，即上台阶分别开挖30 m、40 m、50 m和60 m后再进行下台阶的开挖支护，图7所示为开挖完成后的塑性区分布图。为了更清晰地掌握开挖对隧洞周边围岩的影响规律，为后续支护措施的分析提供安全余量，围岩的物理力学参数略偏保守，因此导致围岩塑性区范围略微偏大。由计算结果可知，总体来说不同台阶长度情况下塑性区分布差别不大，在隧洞断面周边形成以剪切破坏为主的塑性区（绿色单元），该部分塑性区占比较大，但在计算完成后应力集中情况已恢复至弹性区间，在计算完成后仅有集中在隧道两帮和拱脚处的小范围区域仍处于塑性破坏状态（浅蓝色和黑色单元），在施工过程中需要对此范围的支护进行加强。在开挖过程中，左洞拱顶处会出现拉伸破坏区域（黑色方框处），且拉伸破坏区域的范围随着施工台阶长度的增加而增大，当台阶长度从30 m增加至60 m时，拉伸破坏单元数量增加了约一倍。在台阶长度为60 m的模型中，左洞拱顶形成了连续贯通的拉伸破坏区域，且出现较多在计算完成时仍处于破坏状态的单元（黑色单元）。右洞的塑性区具有沿右侧边墙向上方延伸的趋势，而且在侧墙和下方拱脚处均出现了比左洞多的剪切破坏单元（浅蓝色单元），此外，在左洞和右洞拱顶和边墙的交界处均发现了剪切和拉伸复合作用的破坏单元（红色单元）。综合以上分析，60 m台阶长度控制围岩稳定性的效果相对较差，在施工过程中需要对隧道两帮和拱脚处的支护进行加强，如使用较长的锁脚锚杆和强度较高的连接钢筋和连接螺栓。

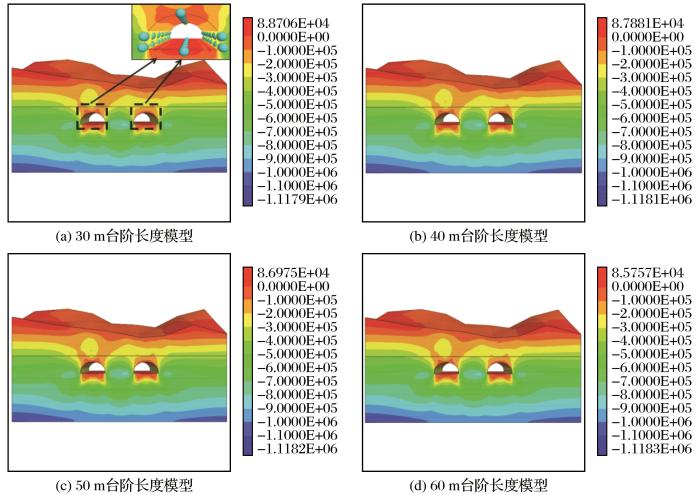
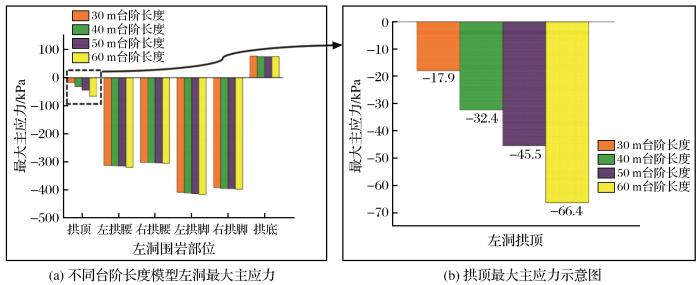
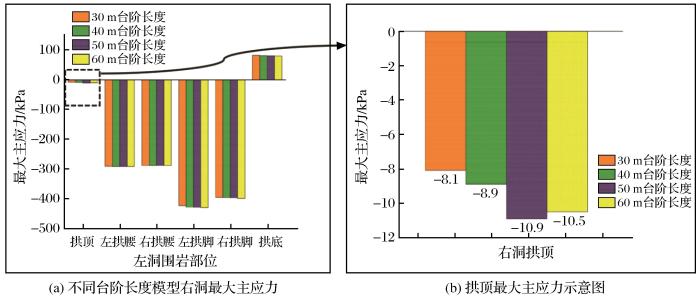
图8所示为不同台阶长度情况下Ⅲ级围岩段隧道开挖完成后的最大主应力云图，总体来说不同台阶长度对最大主应力的分布影响不大。在隧道断面周边的最大主应力呈对称分布，最大主应力沿着拱顶—两帮—拱脚逐渐增加，在拱脚处达到最大，且在拱底出现了较大范围的拉应力。为量化分析台阶长度对最大主应力的影响，在隧道围岩的拱顶、左右拱腰、左右拱脚和拱底中点处设立观测点［如图8（a）右上角示意图所示：沿隧道轴向每隔10 m设置一个观测点，共设立7个观测点，左右洞相同］，对隧道断面周边不同断面处的最大主应力取平均值，得到开挖完成后隧道断面周边不同围岩部位的最大主应力如表3所示，图9和图10分别为左洞和右洞最大主应力柱状图。由图9、图10和表3可知，隧道围岩的最大主应力分布具有以下规律：拱底出现了较小的拉应力，这是由于该隧道断面无仰拱且初期支护只设立在拱顶和拱腰处，拱底之外的最大主应力整体呈现“拱脚>拱腰>拱顶”的趋势，故在施工过程中应加强拱底的支护措施。此外，隧洞左侧拱腰和拱脚的最大主应力均略大于右侧，且右洞拱腰处的最大主应力略大于左洞，而在拱脚处左洞略大于右洞。台阶长度对最大主应力的影响主要体现在拱顶处［图9（b）和图10（b）］：台阶长度每增加10 m，左洞拱顶处最大主应力分别增加14.5，13.3，20.9 kPa，其中台阶长度从50 m增加至60 m的拱顶最大主应力增加值明显较大，不利于控制拱顶处的围岩稳定性，右洞拱顶的最大主应力增加值分别为0.8，2.0，-0.4 kPa，增加值相对较小。

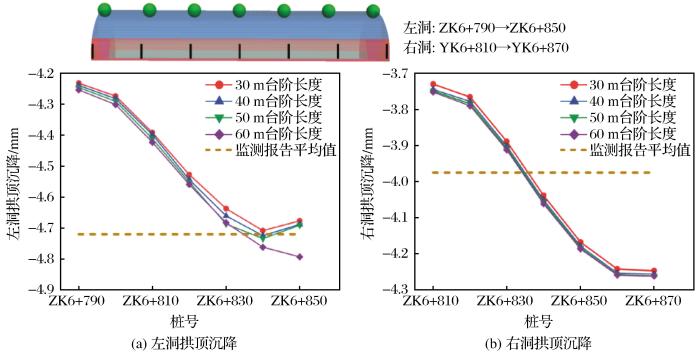
根据图5设立的观测点位置，将模型中设置的观测点1处的竖向位移值作为拱顶沉降指标，观测点2-3的水平收敛值（隧道拱腰向隧道内部净空的位移大小，在数值上等于左拱腰向右的水平位移量+右拱腰向左的水平位移量）与观测点4-5的水平收敛值取平均值作为隧道的水平净空收敛指标，求得该段隧道在围岩变形处于稳定阶段时的观测点位移平均值。不同台阶长度模型数值模拟完成后的最终位移如表4和表5所示，其中竖向位移值为负表示拱顶向下位移，水平收敛值为正表示隧道围岩向隧道净空方向位移。由各台阶长度情况下不同观测断面处的左右洞拱顶沉降量和水平净空收敛量的数值模拟结果（图11和图12）可知，左洞和右洞的拱顶沉降量和水平收敛值均呈现出随台阶长度的增加而增加的趋势，此外，在不同台阶长度的模型中左洞的拱顶竖向位移均大于右洞，而左洞的水平收敛值小于右洞，这与量测报告测得的数据规律一致。由图11（a）可知，30 m、40 m和50 m台阶长度模型的左洞拱顶沉降沿开挖方向先逐渐增加后减小，而60 m台阶长度模型中的沉降量在整个开挖过程中一直保持着增加的趋势，在开挖断面前进50 m之后，60 m台阶长度模型的拱顶沉降值明显大于其他模型，这种情况不利于控制围岩的变形。由图11（b）可知，不同台阶长度模型的右洞拱顶沉降量变化趋势相同，均为先小幅增加再大幅增加最后趋于平稳。

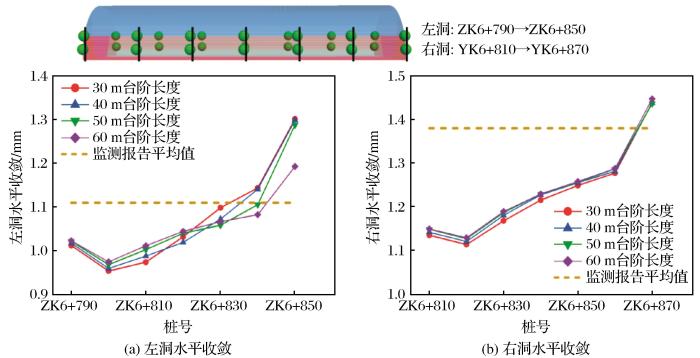
由图12（a）可知，不同台阶长度模型的左洞水平收敛值随着开挖断面向前推进过程中的变化趋势相同，当开挖断面由桩号ZK6+790前进至桩号ZK6+800的过程中，左洞水平收敛呈减小的趋势，此后逐渐增加，但不同模型的增加幅度不同。右洞水平收敛值变化趋势表现为先缓慢减小再小幅增加最后大幅增加，不同台阶长度情况下模型的右洞水平收敛值差距随着开挖断面的前进而逐渐减小。在隧道实际开挖施工过程中台阶长度为50 m左右，在对应观测点1-5位置处对围岩变形量进行了监控量测，利用监测数据计算出该段隧道在围岩变形处于稳定阶段时的监测点位移平均值（图11和图12中虚线所示）：其中左洞的拱顶沉降平均值为4.72 mm，右洞拱顶沉降平均值为3.975 mm，左洞的水平净空收敛值的平均值为1.11 mm，右洞的水平净空收敛值的平均值为1.38 mm。由图11和图12可知，上述数据的数值模拟结果与监测报告的数据较为匹配，验证了数值建模工作的准确性。

系统锚杆的锚杆间距通常采用工程类比法确定（招商局重庆交通科研设计院有限公司，2018），也可以按锚杆长度的0.3~0.5倍取值，三车道锚杆长度规定不小于2.5 m。通过综合对比分析不同台阶长度模型的围岩塑性区、围岩应力和围岩变形，得出该隧道工程台阶法施工方案的最优台阶长度为50 m。在此基础上，为了比较锚杆间距对支护效果的影响，固定台阶长度为50 m，将砂浆锚杆纵距分别设为1.0 m、1.5 m和2.0 m进行仿真分析（现场实际锚杆纵距为1.0 m）。围岩的其他基本支护参数参考施工现场实际情况：砂浆锚杆长度为3.5 m，环距为1.2 m，钢拱架的纵距为1.0 m，喷射混凝土厚度为0.24 m。图13所示为不同锚杆纵距情况下Ⅲ级围岩段隧道开挖完成后模型塑性区分布图，由图13可知，左洞拱顶处的剪切和拉伸复合作用的破坏单元（红色单元）明显多于右洞拱顶，右洞的拱腰处较大部分区域出现了剪切破坏（浅蓝色单元），而左洞拱腰处几乎没有剪切破坏的单元。此外，在左洞右拱脚处均有沿边墙向下延伸的仍处于破坏状态的剪切破坏单元（浅蓝色单元），应加强该围岩部分的支护。由计算结果可知，锚杆纵距增加后右洞的右拱腰处（黑色方框处）仍处于破坏状态的剪切破坏单元（浅蓝色单元）范围明显增大，这是由于初期支护主要分布在拱顶至拱腰的中部，锚杆纵距增加使得锚杆的数量减少，减小了对围岩的支承作用。因此，锚杆纵距的增加会影响初期支护的效果，增加施工过程中的安全风险。

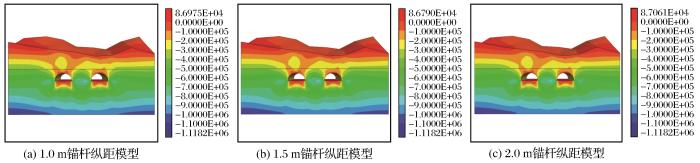
图14所示为不同锚杆纵距模型隧道开挖完成后的最大主应力云图，总体上，左右洞隧道断面周边最大主应力分布特征相似。在隧道断面周边设立与上一节模型一致的观测点［图8（a）右上角示意图］，并对不同断面处的最大主应力取平均值，得到开挖完成后不同隧道部位的最大主应力如表6所示。

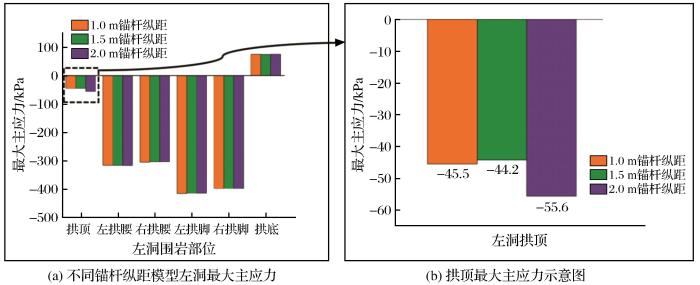
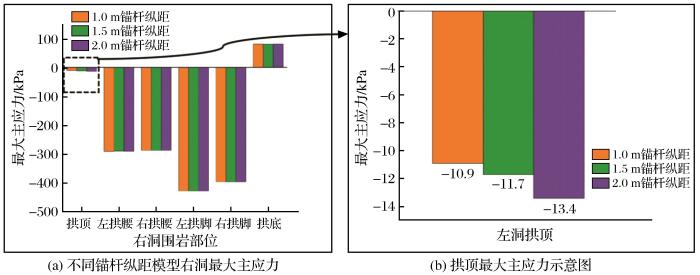
图15和图16分别为根据表6数据制成的左洞和右洞最大主应力柱状图。由图15、图16和表6可知，在拱底处出现了数量级较小的拉应力，拱底之外的部分整体呈现“拱脚>拱腰>拱顶”的趋势，其中左侧拱腰、拱脚的最大主应力均大于右侧，右洞拱腰处的最大主应力略大于左洞，而在左洞拱脚处的最大主应力略大于右洞。改变锚杆纵距的主要区别也体现在拱顶处，在左洞拱顶处，锚杆纵距从1 m增加至2 m，最大主应力增加百分比分别为-2.9%和25.8%，在右洞拱顶处分别为7.5%和14.3%，由此可见，锚杆纵距增加会导致拱顶处最大主应力升高，不利于维持拱顶处的围岩稳定。

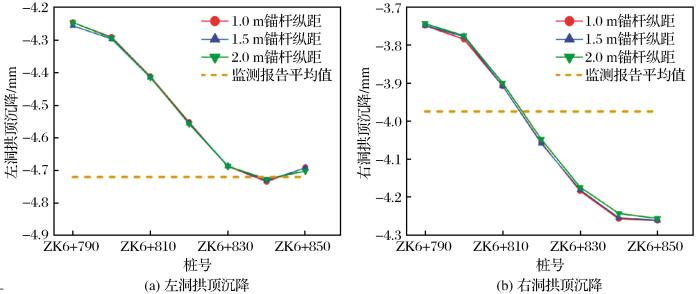
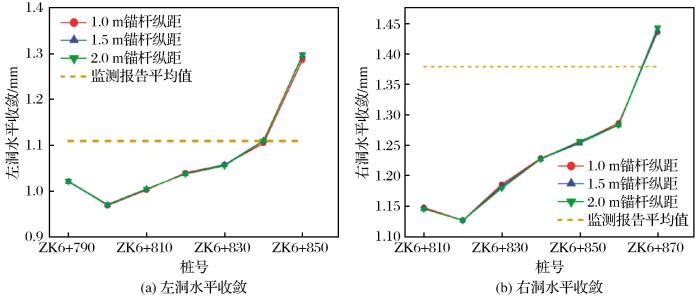
图17和图18所示为不同锚杆纵距情况下左、右洞各观测断面处的拱顶沉降量和水平净空收敛量的对比图。由计算结果可知，左洞拱顶沉降沿开挖方向先增加（ZK6+790~ZK6+840段）后减小（ZK6+840~ZK6+850段），右洞拱顶沉降逐渐增加（YK6+810~YK6+860段）后趋于平稳（YK6+860~ YK6+870段），左、右洞的水平收敛变化趋势相同，均沿开挖方向先减小（左洞ZK6+790~ZK6+800、右洞YK6+810~YK6+820）后逐渐增加（左洞ZK6+800~ZK6+850、右洞YK6+820~YK6+870）。根据以上数值计算结果，说明锚杆纵距的增加对隧道拱顶位移和隧道拱腰水平收敛的影响较小，而锚杆纵距的减小使得对围岩的变形控制能力减小，初期支护中的喷射混凝土和钢拱架需要发挥更强的围岩变形控制能力来维持支护效果，可能导致支护结构的破坏，增加施工过程中的安全风险。不同台阶长度模型数值模拟完成后的最终位移如表7和表8所示，数值模拟结果与监控量测报告的位移平均值较匹配。

本文对某超大断面扁平结构隧道的Ⅲ级围岩段进行数值建模，分析开挖过程中围岩塑性区、围岩应力和围岩变形的变化规律，讨论上下台阶法施工方案中改变台阶长度和锚杆纵距2种施工参数对隧道围岩稳定性的影响，结合现场施工的监测报告验证了实际施工参数的合理性。本文数值模型的计算结果不仅在数值上与工程监测数据相匹配，隧道左右洞的围岩变形规律也与之相对应，验证了模型建立的正确性，对类似工程具有较好的参考价值。本文得出的主要结论如下：

（1）不同台阶长度和不同锚杆纵距情况下，在左洞和右洞拱顶和边墙的交界处均发现了剪切和拉伸复合作用的破坏区域。此外，在左洞右拱脚处均有沿边墙向下延伸的仍处于破坏状态的剪切破坏单元，因此需要对此范围进行加强支护。

（2）隧洞周边的最大主应力整体呈现“拱脚>拱腰>拱顶”的变化趋势，拱底出现了较小的拉应力，故在施工过程中应加强拱底平面的支护措施。台阶长度或锚杆纵距的增加会导致拱顶处最大主应力产生较大的增幅，不利于控制拱顶处的围岩稳定性。

（3）整体上左洞和右洞的拱顶沉降量和水平收敛值均随台阶长度的增加而增加，在隧道的后半段左洞的水平收敛值随台阶长度的变化趋势相反。锚杆纵距的增加需要初期支护中的其他支护结构发挥更强的围岩变形控制能力，可能导致支护结构的破坏。综合考虑施工效率和围岩稳定等因素，采用台阶长度为50 m和锚杆纵距为1 m的施工参数较为合理。