矿石粒度是选矿过程控制的关键参数之一,也是衡量破碎效果的重要参考依据,实时检测矿石粒度对矿石破碎工艺的优化具有重要意义(李鸿翔等,2021;王伟等,2023;Zhang et al.,2023)。矿石粒度完整样本标签通常需要通过人工筛分方法获取,该方法不仅浪费大量的人力资源,而且效率低下。在有限的有标签样本条件下,传统全监督建模方法的训练能力受到限制,建立高精度、高稳健性的预测模型具有一定难度(徐永洋等,2020;Hu et al.,2022)。因此,面向矿石粒度检测,传统全监督建模方法受到有标签样本稀缺的限制,大量基于图像识别矿石粒度的无标签样本未被有效利用,通过半监督学习有效利用无标签样本构建模型的策略优势凸显。
半监督学习的核心理念在于利用未标记样本信息,通过获得伪标签方式扩展有限的标记样本集合,从而提高模型泛化能力,核心在于如何有效评估伪标签的准确性(Hu et al.,2021;黄发明等,2021)。Kang et al.(2016)建立了基于自训练的半监督支持向量回归(SS-SVR)模型,利用概率局部重构(PLR)模型获得伪标签的方式扩充数据集。史旭东等(2020)提出了基于改进自训练算法的高斯过程回归(GPR)软测量建模方法,先利用相似度估计无标签样本缺失的主导变量值后再筛选估计样本,将泛化能力强的伪标签样本加入有标签样本集后建立软测量模型。毛耿旋等(2022)提出了一种基于半监督回归的高光谱土壤重金属质量浓度反演模型,试验结果表明,在较少标签样本情况下,通过引入大量的未标签样本进行半监督回归分析,能够有效提升模型反演精度。但上述方法采用传统单一学习器构建预测模型,存在一定的局限性,需进一步提升其泛化能力。
本文提出采用融合全监督学习的半监督矿石粒度预测算法。根据矿石样本特征选择不同的回归模型并进行初始化;采用模型性能评估策略获得高置信度伪标签样本;利用伪标签样本与原始标签样本集构建矿石粒度预测模型。
1 基于半监督学习的矿石粒度预测算法
1.1 试验数据分析
矿石经过破碎筛分、碎磨分级和分选加工后,形成碎散物料群体,其颗粒大小和形状多种多样,为描述这些特性,通常使用“粒度” “粒级”“粒度组成”和“平均粒度”等术语(Chun et al.,2021;卢佳旺,2023)。本文选用粒级、加权算术平均粒度、标准差和偏差系数4种指标作为矿石粒度输入特征,综合运用这4种指标可以比较全面地描述矿石的粒度特性。其中,加权算术平均粒度、标准差和偏差系数的计算公式为
式中:
在某选厂细碎皮带上采集+10 mm、+5~10 mm和-5 mm共3种不同矿石粒级的实测数据集,数据结构如表1所示(部分数据),其中人工筛分矿石粒度分布为有标签样本,图像识别矿石粒度分布为无标签样本,数据集包含63个有标签样本,288个无标签样本。其中有标签矿石粒度分布样本训练集、验证集和测试集划分比例为2∶1∶1。
表1 矿石粒度数据集数据结构(部分数据)
Table 1
| 样本数据类型 | 矿石粒级 /mm | 图像识别 矿石粒度 分布/% | 加权算术平均粒度 /mm | 标准差 | 偏差 系数 | 人工筛分 矿石粒度 分布/% |
|---|---|---|---|---|---|---|
有标签样本 数据 | +10 | 0.322 | 3.245 | 1.586 | 0.244 | 0.290 |
| +5~10 | 0.315 | 2.434 | 1.190 | 0.183 | 0.285 | |
| -5 | 0.363 | 0.811 | 0.397 | 0.061 | 0.425 | |
| +10 | 0.501 | 4.019 | 1.267 | 0.158 | 0.474 | |
| +5~10 | 0.356 | 3.014 | 0.950 | 0.118 | 0.312 | |
| -5 | 0.143 | 1.005 | 0.317 | 0.039 | 0.214 | |
| … | ||||||
无标签样本 数据 | +10 | 0.359 | 3.421 | 1.548 | 0.226 | |
| +5~10 | 0.330 | 2.566 | 1.161 | 0.170 | ||
| -5 | 0.311 | 0.855 | 0.387 | 0.057 | ||
| +10 | 0.325 | 3.286 | 1.582 | 0.241 | ||
| +5~10 | 0.318 | 2.465 | 1.187 | 0.181 | ||
| -5 | 0.357 | 0.822 | 0.396 | 0.060 | ||
| +10 | 0.366 | 3.468 | 1.504 | 0.221 | ||
| +5~10 | 0.338 | 2.601 | 1.148 | 0.166 | ||
| -5 | 0.296 | 0.867 | 0.383 | 0.055 | ||
| … |
不同学习器预测性能分析。应用融合全监督学习的半监督矿石粒度预测算法中,学习器的选择和组合方式至关重要,影响整个模型最终的预测性能,选择合适的学习器及其组合方式,可建立有效地融合全监督学习的半监督预测模型(Liu et al.,2022;庄慧敏,2022)。
为获取适用的学习器,需要观测各个模型对实际矿石粒度数据集单独预测的效果。这一过程需要每个模型的超参数达到最优,参考文献选用5折交叉验证,结合GridSearchCV(网格调参方法)以确定最佳超参数组合,并添加L2正则化项防止模型过拟合(宋建等,2022)。
回归模型的预测性能可通过矿石粒度预测数据与人工筛分粒度数据的偏差来评估,采用均方根误差(Root Mean Squared Error,RMSE)和平均绝对误差(Mean Absolute Error,MAE)作为评价标准,范围为[0,+∞)。当矿石预测粒度分布与人工筛分粒度分布完全吻合时,所建立的回归模型为完美模型;误差越大,该值越大(兰凤崇等,2023)。均方根误差和平均绝对值误差计算公式为
式中:
应用采集到的有标签样本数据,选择9种常用学习器的最佳超参数及预测误差,如表2所示。其中,决策树(Tree)、梯度提升决策树(GBDT)、贝叶斯回归(Bayes)、岭回归和BP神经网络的预测性能较为突出,随机森林(RF)、XGBoost、多项式回归和支持向量机(SVM)的预测误差相对较大。
表2 各模型的最佳超参数及预测误差
Table 2
| 模型 | 最佳超参数 | RMSE | MAE |
|---|---|---|---|
| Tree | max_depth = 4 | 0.030 | 0.026 |
| RF | n_estimators = 20 | 0.040 | 0.027 |
| GBDT | learning_rate = 0.01 max_depth = 5 n_estimators = 200 | 0.026 | 0.022 |
| XGBoost | gamma = 0.0 max_depth = 4 min_child_weight = 4 n_estimators = 70 | 0.040 | 0.028 |
| Bayes | alpha_1= 1e-08 alpha_2= 1e-06 lambda_1= 1e-06 lambda_2= 1e-08 n_iter= 100 | 0.029 | 0.022 |
| 多项式回归 | Linearregression_fit _intercept= True polynomialfeatures_degree2 | 0.080 | 0.051 |
| 岭回归 | Alpha = 0.3 gamma = 0.1 kernel = linear | 0.030 | 0.023 |
| SVM | C = 1.0 Gamma = 1.0 Kernel = linear | 0.075 | 0.063 |
| BP神经网络 | Activation = relu Alpha = 0.0001 hidden_layer_sizes = (100,) | 0.030 | 0.023 |
为进一步选择合适的学习器,利用决定系数(
表3 5种预测模型在实际矿石数据集上的决定系数
Table 3
| 模型 | |
|---|---|
| Tree | 0.871 |
| GBDT | 0.899 |
| Bayes | 0.869 |
| 岭回归 | 0.867 |
| BP神经网络 | 0.872 |
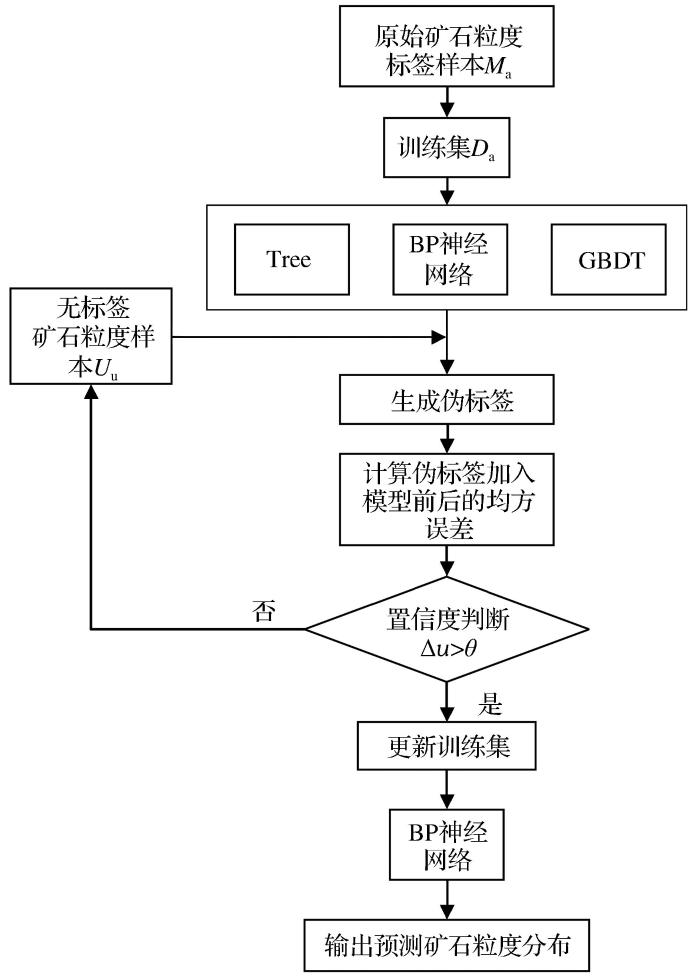
1.2 算法流程
图1
算法流程为:首先,通过对原始矿石粒度标签样本
1.3 算法实现
(1)初始回归模型构建模块
原始矿石粒度标签样本记为
通过分层抽样方法对
①构建Tree回归模型
将
式中:
式中:
通过求解
②构建GBDT回归模型
初始化一个基学习器
式中:
建立一系列CART回归树,利用梯度提升技术拟合残差,在第
故残差估计值
确定残差估计值后,利用CART回归树进行拟合,得到第z棵树的叶节点区域为
更新学习器
式中:
迭代结束后,形成GBDT强学习器
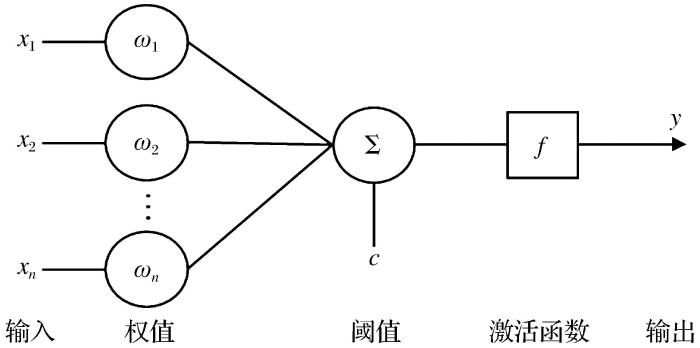
③构建BP神经网络
BP神经网络中每个神经元的结构模型如图2所示。
图2
其数学模型可表示为
式中:
(2)伪标签样本获取模块
无标签矿石粒度样本
基于初始回归决策树、GBDT和BP神经网络模型获得无标签样本
然后,由伪标签和
获取伪标签样本后,需要判断该伪标签样本加入训练集
伪标签样本(
(
式中:
显然,
重复上述针对单个无标签样本的评估过程,将通过上述过程加入训练集
(3)预测模块
基于混合样本集
2 试验及结果分析
表4 高置信度伪标签样本数据(部分数据)
Table 4
矿石粒级 /mm | 图像识别矿石粒度分布/% | 加权算术平均粒度/mm | 标准差 | 偏差 系数 | 模型预测矿石粒度分布/% |
|---|---|---|---|---|---|
| +5~10 | 0.33 | 2.566 | 1.161 | 0.170 | 0.318 |
| -5 | 0.357 | 0.822 | 0.396 | 0.060 | 0.377 |
| +10 | 0.366 | 3.468 | 1.504 | 0.221 | 0.285 |
| -5 | 0.296 | 0.867 | 0.383 | 0.055 | 0.393 |
| +10 | 0.311 | 3.167 | 1.606 | 0.254 | 0.297 |
| -5 | 0.389 | 0.792 | 0.401 | 0.063 | 0.279 |
| +10 | 0.305 | 3.156 | 1.600 | 0.254 | 0.302 |
| +5~10 | 0.305 | 2.367 | 1.200 | 0.190 | 0.416 |
| +5~10 | 0.321 | 2.515 | 1.176 | 0.175 | 0.350 |
| -5 | 0.332 | 0.838 | 0.392 | 0.059 | 0.318 |
| +10 | 0.366 | 3.468 | 1.530 | 0.221 | 0.386 |
| +5~10 | 0.340 | 2.601 | 1.148 | 0.166 | 0.280 |
| -5 | 0.360 | 0.803 | 0.388 | 0.060 | 0.324 |
| +10 | 0.310 | 3.363 | 1.507 | 0.224 | 0.402 |
| +5~10 | 0.380 | 2.522 | 1.130 | 0.168 | 0.282 |
| -5 | 0.310 | 0.841 | 0.377 | 0.056 | 0.305 |
| +10 | 0.310 | 3.313 | 1.535 | 0.232 | 0.415 |
| -5 | 0.250 | 0.903 | 0.367 | 0.058 | 0.325 |
| +5~10 | 0.380 | 2.606 | 1.114 | 0.160 | 0.396 |
| +5~10 | 0.390 | 2.569 | 1.114 | 0.163 | 0.325 |
| +10 | 0.300 | 3.150 | 1.596 | 0.253 | 0.388 |
| -5 | 0.390 | 0.788 | 0.399 | 0.063 | 0.282 |
| … |
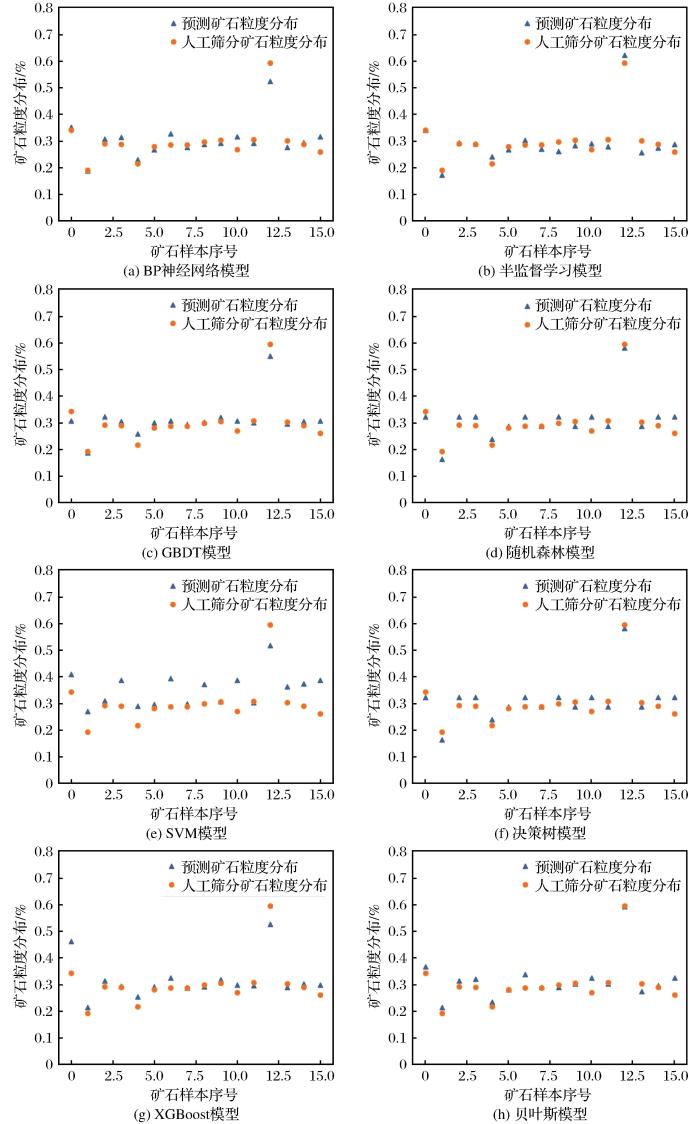
图3
表5 8种预测模型的评价指标对比
Table 5
| 模型 | 评价指标 | ||
|---|---|---|---|
| RMSE | MAE | ||
| BP神经网络 | 0.031 | 0.027 | 0.862 |
| 半监督学习模型 | 0.023 | 0.020 | 0.921 |
| GBDT | 0.030 | 0.024 | 0.871 |
| RF | 0.041 | 0.033 | 0.756 |
| SVM | 0.046 | 0.034 | 0.692 |
| 决策树 | 0.029 | 0.025 | 0.882 |
| XGBOOST | 0.030 | 0.025 | 0.872 |
| 贝叶斯 | 0.029 | 0.022 | 0.879 |
为了进一步分析算法性能,在半监督学习算法结构中选用不同模型的组合方式作为预测模块中的预测模型,并使用RMSE、MAE和
表6 不同组合预测模型测试性能对比
Table 6
| 模型 | 评价指标 | ||
|---|---|---|---|
| RMSE | MAE | ||
| 半监督+决策树 | 0.031 | 0.027 | 0.862 |
| 半监督+BP | 0.023 | 0.020 | 0.921 |
| 半监督+GBDT | 0.030 | 0.024 | 0.871 |
| 半监督+RF | 0.041 | 0.033 | 0.756 |
| 半监督+XBGoost | 0.046 | 0.034 | 0.692 |
| 半监督+贝叶斯 | 0.029 | 0.025 | 0.882 |
| 半监督+岭回归 | 0.030 | 0.025 | 0.872 |
由表6可知,相比其他组合方式,本文选用的半监督+BP神经网络方法的RMSE、MAE最低,较半监督+决策树分别降低了25.81%和25.93%,较半监督+RF分别降低了43.90%和39.39%;本文方法决定系数
3 结论
(1)针对矿石粒度检测中传统全监督建模方法存在有标签样本稀缺,同时大量无标签样本未被有效利用的问题,利用原始矿石粒度有标签样本训练决策树、GBDT和BP神经网络3种预测模型;对无标签矿石粒度样本进行置信度判断,选择出高置信度的无标签矿石粒度样本添加到原始矿石粒度样本中,同时在无标签矿石粒度样本中删除相应的样本,利用更新后的原始矿石粒度样本训练BP神经网络,以提高预测模型的预测精度。
(2)相比决策树、岭回归和贝叶斯等传统全监督建模方法,融合全监督学习的半监督矿石粒度预测方法模型决定系数分别提高了5.0%、5.4%和5.2%,RMSE分别下降了23.33%、23.33%和20.69%,MAE分别下降了23.08%、13.04%和9.09%,验证了融合全监督学习的半监督矿石粒度预测模型的可行性和可靠性。
(3)针对有标签矿石粒度样本数据获取耗时耗力问题,提出了融合全监督学习的半监督矿石粒度预测模型,相比传统全监督预测模型,该模型更适用于矿石粒度预测,准确率显著提升。
http://www.goldsci.ac.cn/article/2024/1005-2518/1005-2518-2024-32-3-539.shtml
参考文献
Numerical study on crushing law of iron ore under different impact velocity using CDEM
[J].
Multi granularity based label propagation with active learning for semi-supervised classification
[J].
Semi-supervised patent text classification method based on improved Tri-training algorithm
[J].
SimPLE:Similar pseudo label exploitation for semi-supervised classification
[C]//
Landslide susceptibility prediction modelling based on semi-supervised machine learning
[J].
Semi-supervised support vector regression based on self-training with label uncertainty:An application to virtual metrology in semiconductor manufacturing
[J].
Prediction of remaining useful life of real-world vehicle lithium-ion power battery based on Aseq2seq-PF
[J].
Ore image segmentation method based on GAN-UNet
[J].
A semi-supervised soft sensor method based on vine copula regression and tri-training algorithm for complex chemical processes
[J].
Study on Complex Particle Swarm Space Image Reconstruction and Screening Performance Evaluation in Screening Process
[D].
Hyperspectral inve-rsion of soil heavy metal mass concentration based on semi-supervised regression
[J].
Semi-supervised gaussian process regression modeling based on improved self-training algorithm
[J].
Injection molded part size prediction method based on stacking integrated learning
[J].
Research on thermal error of CNC machine tool feed system based on CNN-GRU combined neural network
[J].
Prediction on composite interface bonding strength between ceramsite lightweight aggregate concrete and normal concrete based on GBDT algorithm
[J].
A survey of ore image processing based on deep learning
[J].
Soft sensor of dioxin emission concentration based on Bagging semi-supervised deep forest regression
[J].
Prediction of copper mineralization based on semi-supervised neural network
[J].
Influence of ore size on the production of micro-sized ore particles by high-pressure gas rapid unloading
[J].
Research on Semi-Supervised Learning Based ARP Attack Detection Method in SDIIoT
[D].
基于改进三体训练法的半监督专利文本分类方法
[J].
基于半监督机器学习的滑坡易发性预测建模
[J].
基于Aseq2seq-PF的实车锂离子动力电池剩余使用寿命预测
[J].
基于GAN-UNet的矿石图像分割方法
[J].
筛分过程复杂粒群空间图像重构与筛分效果评价研究
[D].
基于半监督回归的高光谱土壤重金属质量浓度反演
[J].
基于改进自训练算法的半监督GPR软测量建模
[J].
基于Stacking集成学习的注塑件尺寸预测方法
[J].
基于CNN-GRU组合神经网络的数控机床进给系统热误差研究
[J].
基于GBDT算法的混凝土叠合面黏结强度预测分析
[J].
基于深度学习的矿石图像处理研究综述
[J].
基于Bagging半监督深度森林回归的二噁英排放浓度软测量
[J].
基于半监督神经网络的铜矿预测方法
[J].
软件定义工业物联网下基于半监督学习的ARP攻击检测方法研究
[D].





 甘公网安备 62010202000672号
甘公网安备 62010202000672号