基于神经网络与遗传算法的多目标充填料浆配比优化

doi:10.11872/j.issn.1005-2518.2019.04.581

基于神经网络与遗传算法的多目标充填料浆配比优化

肖文丰^,, 陈建宏^,, 陈毅, 王喜梅

中南大学资源与安全工程学院，湖南长沙 410083

Optimization of Multi-objective Filling Slurry Ratio Based on Neural Network and Genetic Algorithm

XIAO Wenfeng^,, CHEN Jianhong^,, CHEN Yi, WANG Ximei

School of Resources and Safety Engineering, Central South University, Changsha 410083, Hunan, China

通讯作者: 陈建宏（1963-），男，江苏苏州人，教授，从事矿业经济和采矿系统工程研究工作。cjh@263.net

收稿日期: 2019-03-22 修回日期: 2019-05-23 网络出版日期: 2019-08-08

基金资助:

国家自然科学基金青年基金项目“基于人工智能的矿山技术经济指标动态优化”.  51404305
国家自然科学基金项目“基于属性驱动的矿体动态建模及更新方法研究”.  51504286
中国博士后科学基金面上项目“辰州矿业采掘计划可视化编制与优化研究”.  2015M 572269
湖南省科技计划项目“辰州矿业采掘计划可视化编制与优化研究”.  2015RS4060

Received: 2019-03-22 Revised: 2019-05-23 Online: 2019-08-08

作者简介 About authors

肖文丰（1997-），男，湖北孝感人，硕士研究生，从事矿业经济和采矿系统工程研究工作951630775@qq.com , E-mail：951630775@qq.com

摘要

随着充填法在地下矿山开采中的应用越来越广，在满足充填体强度要求的情况下，寻找生产成本最低的充填料浆配比对于矿山生产经营十分重要。基于人工神经网络和遗传算法提出了一种新的充填料浆配比优化方法。首先，以水泥质量分数、粉煤灰质量分数和尾砂质量分数3个充填料浆配比参数为优化参数，以充填体强度为优化目标，建立了3-9-1的BP神经网络，并基于遗传算法对BP神经网络进行优化，建立起预测精度更高的GA_BP神经网络。然后，将预测精度更高的GA_BP神经网络作为适应度函数，结合成本计算函数，通过遗传算法进行多目标优化以获取最优的充填料浆配比参数。结果表明：当充填体抗压强度为1.5 MPa时的成本最低，充填料浆配比组合为水泥质量分数为8%，粉煤灰质量分数为2.3%，尾砂质量分数为66.3%，最低成本为29.3元/t，优化结果与实际情况一致。

关键词： 充填体抗压强度 ; 充填法 ; 充填料浆配比优化 ; GA_BP神经网络 ; 遗传算法 ; 多目标优化

Abstract

As the mining depth continues to increase, the pressure management of the stope and goaf is becoming more and more difficult.In order to maintain the stability of the stope,ensure the safety of the operation and prevent the collapse of the goaf,the filling method has become the preferred method for underground mining and has been widely applied.The filling method is to fill the filling body in the goaf to form a filling body with a certain compressive strength, and then carry out underground management by the supporting action of the filling body.Therefore, in the process of mining using the filling method, it is the key to efficient and safe mining of the mine to prepare the filling slurry with reasonable ratio and considerable economy to ensure that the compressive strength of the filling body can meet the needs of ground pressure management.However, there is no simple linear mapping between the filling ratio and the compressive strength of the filling body, and it is usually difficult to calculate by general mathematical methods.To this end, many researchers have conducted a lot of research on the ratio of filling slurry and the optimization of compressive strength of the filling body.Most of these studies only consider optimization under single-objective conditions, and there are few studies on multi-objective conditions.Therefore, other methods should be found to carry out multi-objective optimization research. In this paper, based on artificial neural network and genetic algorithm, a new optimization method of filling ratio is proposed.Firstly, the parameters of cement filling ratio, fly ash mass fraction and tailings mass fraction were optimized parameters, and the backfill strength was used as the optimization target to establish a BP neural network of 3-9-1.The BP neural network is optimized based on genetic algorithm, and the GA_BP neural network with higher prediction accuracy was established.Then,the GA_BP neural network with higher prediction accuracy is used as the fitness function, combined with the cost calculation function, and multi-objective optimization is performed by genetic algorithm to obtain the optimal filling slurry ratio parameter.The results show that when the compressive strength of the filling body is 1.5 MPa, the cement mass fraction is 8%, the fly ash mass fraction is 2.3%, the tailings mass fraction is 66.3%, the cost is the lowest, and the lowest cost is 29.3 yuan/t.The optimization results are consistent with the actual situation.

Keywords： filling body compressive strength ; filling method ; filling slurry ratio optimization ; GA_BP neural network ; genetic algorithm ; multi-objective optimization

PDF (1098KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

肖文丰, 陈建宏, 陈毅, 王喜梅. 基于神经网络与遗传算法的多目标充填料浆配比优化[J]. 黄金科学技术, 2019, 27(4): 581-588 doi:10.11872/j.issn.1005-2518.2019.04.581

XIAO Wenfeng, CHEN Jianhong, CHEN Yi, WANG Ximei. Optimization of Multi-objective Filling Slurry Ratio Based on Neural Network and Genetic Algorithm[J]. Gold Science and Technology, 2019, 27(4): 581-588 doi:10.11872/j.issn.1005-2518.2019.04.581

随着矿山开采深度的不断增加，采场和采空区地压管理难度也越来越大。为了维护采场稳定性、保障作业安全性和防止采空区塌陷等，充填法成为地下矿山开采的首选方法并得到广泛应用^[1,2]。充填法是通过在采空区注入充填料浆以形成具有一定抗压强度的充填体，然后依靠充填体的支撑作用进行地下管理。因此，在运用充填法进行矿山开采的过程中，制备出配比合理、经济可观的充填料浆，以确保充填体的抗压强度能够满足地压管理的需要是矿山进行高效安全开采的关键。但充填料浆配比与充填体抗压强度之间不是简单的线性映射关系，通常很难用一般的数学方法进行计算^[3,4,5,6]。为此，许多研究人员针对充填料浆配比与充填体抗压强度优化问题开展了大量研究。例如：吴浩等^[7]运用响应面—满意度函数耦合理论和采用Box-Behnken实验设计方法对某铁矿尾砂胶结充填材料的最优配比进行研究，得到了该矿尾砂胶结充填材料的最优配比。赵国彦等^[8]就采场温度、灰砂质量比和固相质量分数对高寒地区矿山充填料浆的强度特性和流动特性的影响进行研究，得到了高寒矿山不同采场温度下最佳灰砂质量和充填料浆输送浓度。张钦礼等^[9]通过配比试验与BP神经网络预测模型相结合的方式对充填料浆配比进行研究，找出了强度合理的最优充填料浆配比。这些数学模型虽在优化充填料浆配比方面取得了一定的效果，但均为单目标优化，在优化抗压强度的同时并没有考虑生产成本，因此应寻找其他方法开展多目标优化的研究工作^[10,11,12]。

本文基于已有数据集，构建能够表达充填料浆配比与抗压强度之间非线性关系的BP神经网络模型，为提高BP神经网络的预测精度，将遗传算法用于优化神经网络的权值和阈值以构建GA_BP神经网络，优化结果表明，GA_BP神经网络预测精度明显高于传统的BP神经网络。将构建好的GA_BP神经网络与充填料浆成本函数用作适应度函数，基于带精英策略的快速非支配排序遗传算法多目标寻优，寻找满足工程需要的抗压强度下经济最优的充填料浆配比。

1 抗压强度预测的BP神经网络构建

1.1 样本数据收集与处理

神经网络对训练样本数据的质量要求高，训练样本的好坏直接决定了神经网络的泛化能力^[13,14,15]。本文从某矿山充填料浆配比试验中选取24组试验数据^[9]，表1为充填料浆配比学习样本数据，表2为充填料浆配比归一化后的样本数据。其中，影响充填体抗压强度的充填体料浆配比参数为水泥的质量分数（ω₁）、粉煤灰的质量分数（ω₂）和尾砂的质量分数（ω₃），将试验数据中的1~21组用作神经网络训练集，22~24组用作测试集。隐含层采用Sigmoid函数，输出层采用Purelin函数。由于Sigmoid函数值域范围是[-1,1]或[0,1],因此将训练样本输入到神经网络时，为了避免数据由于量纲不同而产生的较大误差，需利用式（1）对数据进行归一化处理。

表1 充填料浆配比学习样本数据

Table 1 Filling slurry ratio data of learning samples

参数	序号
参数	1	2	3	4	5	6	7	8	9	10	11	12
ω₁	15.20	14.80	14.00	10.86	10.00	8.44	8.22	7.78	6.91	6.73	4.69	4.38
ω₂	0	0	0	0	0	0	0	0	0	0	0	0
ω₃	60.80	59.20	56.00	65.14	60.00	67.56	65.78	62.22	69.09	67.27	70.31	67.50
抗压强度/MPa	3.67	3.64	2.89	2.43	1.64	1.59	1.54	1.48	1.14	0.84	0.54	0.43
参数	序号
参数	13	14	15	16	17	18	19	20	21	22	23	24
ω₁	4.38	7.78	8.44	8.67	6.36	6.91	3.50	3.80	10.57	6.36	7.09	3.90
ω₂	0	15.56	16.89	17.73	12.73	13.82	14.00	15.20	0	0	14.18	15.60
ω₃	65.63	46.67	50.67	52.00	50.91	55.27	52.50	57.00	63.43	63.64	56.73	58.50
抗压强度/MPa	0.43	0.43	2.31	2.21	1.49	1.67	0.53	0.67	2.28	0.90	1.85	0.74

新窗口打开| 下载CSV

表2 充填料浆配比归一化后的样本数据

Table 2 Normalized samples data of filling slurry ratio

参数	序号
参数	1	2	3	4	5	6	7	8	9	10	11	12
ω₁	1	0.965	0.897	0.629	0.555	0.422	0.403	0.365	0.291	0.276	0.101	0.085
ω₂	0	0	0	0	0	0	0	0	0	0	0	0
ω₃	0.597	0.530	0.394	0.781	0.563	0.883	0.808	0.657	0.948	0.871	1	0.881
抗压强度/MPa	3.67	3.64	2.89	2.43	1.64	1.59	1.54	1.48	1.14	0.84	0.54	0.43
参数	序号
参数	13	14	15	16	17	18	19	20	21	22	23	24
ω₁	0.075	0.365	0.422	0.441	0.244	0.291	0	0.025	0.604	0.244	0.306	0.034
ω₂	0	0.897	0.974	1	0.734	0.797	0.807	0.877	0	0	0.818	0.900
ω₃	0.802	0	0.169	0.225	0.179	0.363	0.246	0.437	0.709	0.717	0.425	0.500
抗压强度/MPa	0.43	1.85	2.13	2.21	1.49	1.67	0.53	0.67	2.28	0.9	1.85	0.74

新窗口打开| 下载CSV

\bar{x_{i}} = \frac{x_{i} - x_{m i n}}{x_{m a x} - x_{m i n}}

（1）

1.2 BP神经网络结构设计

输入层神经元选择是影响网络预测效果的主要因素^[16,17]。神经网络的输入参数为充填料浆配比参数ω₁、ω₂和ω₃，输出参数为充填体抗压强度，输入层神经元个数为3，输出层神经元个数为1。隐含层神经元个数在国际上没有很好的确定办法，本文先采用式（2）估算出隐含层神经元数目范围，再利用“试凑法”，以相对误差为衡量准则，选取神经元数目范围内误差最小的隐含层神经元个数。

n_{1} = \sqrt[]{n + m} + a

（2）

式中：输入参数n为输入层神经元个数；m为输出层神经元个数；a为[1,10]之间的常数；输出参数n₁为隐含层神经元个数。

通过式（2）可得隐含层神经元个数在[3,12]之间，再对含有不同隐含层神经元个数的神经网络模型进行误差分析。为保证结果的客观准确，每个模型的误差都是训练10次后的平均误差。选取的误差评价指标为相对平均误差，其定义如下：

M A E = \frac{1}{N} \sum_{i = 1}^{N} \frac{|y_{i}' - y_{i}|}{y_{i}}, i = 1,2, . . ., n

（3）

式中：N为样本个数，y_i'和y_i分别表示预测值和期望值。

误差分析如表3所示，可以直观地看出，当隐含层神经元个数为9(网络结构为3-9-1)时，神经网络误差最小。

表3 不同隐含层神经元数的网络误差对比

Table 3 Comparison of network errors for number of neurons in different hidden layers

网络结构	误差	迭代次数	网络结构	误差	迭代次数
3-4-1	0.2838	159	3-9-1	0.1768	91
3-5-1	0.2298	87	3-10-1	0.1791	120
3-6-1	0.2238	79	3-11-1	0.1959	94
3-8-1	0.1961	123	3-12-1	0.2022	48

新窗口打开| 下载CSV

1.3 BP神经网络参数设计

BP神经网络的构建，首要任务是选择对网络训练有很大影响的学习速率，如果学习速率选择过小，将会大幅增加网络的训练时间；如果学习速率选择过大，则很可能会使得网络输出在最优值之间震荡，甚至会远离最优值而使网络无法收敛^[18]。因此，本文将学习速率设为0.1，并选用学习速率可以改变的梯度下降算法“traingda”。同时，通过大量试验，隐含层的传递函数选用“tansig”，输出层的传递函数选用线性函数“purelin”，训练次数设为1 000。

2 遗传算法优化BP神经网络

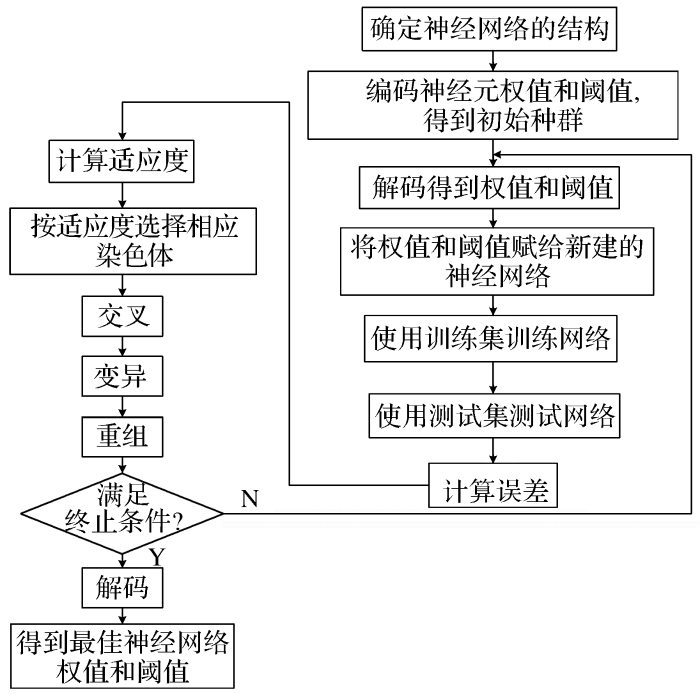
遗传算法（Genetic Algorithm）不同于以往的搜索算法，它是一种模拟自然界“适者生存”的进化算法^[19,20]。遗传算法会将问题参数随机编码成染色体，染色体通常由一维的串结构数据来表示，串上的各个位置对应基因的取值。一般每一代所有的染色体组成一个种群，同一种群中的染色体之间通过交叉、变异及选择操作交换信息，迭代出更优的下一代种群。经过多次迭代后，种群中的染色体将收敛于最优的染色体^[12]。染色体的优良程度由适应度函数来评判，染色体越优则适应度值越大，即这个染色体代表的解更优，被遗传给下一代的概率也会更高。

2.1 构建GA_BP神经网络

神经网络的预测精度与初始权值和阈值密切相关，而BP神经网络的初始权值和阈值又是随机给定的，这给BP神经网络的预测带来了很大的不确定性^[21]，所以在将BP神经网络用于遗传算法的适应度函数之前，应先确定最优的初始权值和阈值，以保证神经网络的预测精度。因此，本文在构建BP神经网络的基础上，使用遗传算法优化其权值与阈值，进一步建立预测精度更高的GA_BP神经网络。图1为构建GA_BP神经网络的流程图。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 GA_BP神经网络构建流程图

Fig.1 Flow chart of GA_BP neural network construction

（1）初始种群生成。根据已建立BP神经网络的3-9-1结构可得，需要优化的权值个数为：3×9+9×1=36个，阈值个数为：9+1=10个，待优化参数共46个，如表4所示。参数的编码方式为二进制，将每一个待优化的参数均编码成10位的二进制串，一个染色体由46个参数和460个二进制编码组成，其中1~270位代表输入层到隐含层的权值，271~360位代表隐含层的阈值，361~450位代表隐含层到输出层的权值，451~460位代表输出层阈值。

表4 待优化参数及数量

Table 4 Parameters to be optimized and their quantity

参数	数量/个
输入层与隐含层连接权值数量	27
隐含层阈值数量	9
隐含层与输出层连接权值数量	9
输出层阈值数量	1

新窗口打开| 下载CSV

（2）适应度函数。遗传算法在迭代过程中，基本不会接受外界的信息，因此适应度函数的选取对收敛速度和寻找最优解起到了决定性的作用^[22]。设本模型适应度函数为

F = \frac{1}{|Y_{1} - Y_{2}|}

（4）

式中:Y₁为实际输出值；Y₂为期望输出值。

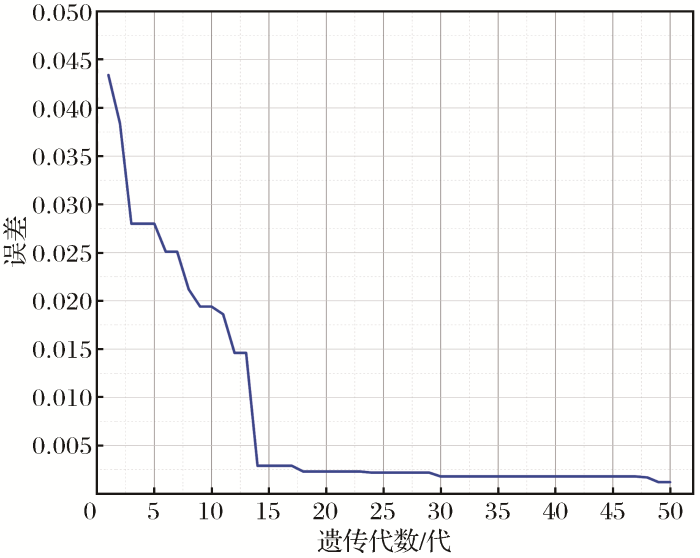
（3）遗传算子。选择操作是模拟自然界的“物竞天择”，适应度值高的染色体更能适应环境，将优良基因遗传给下一代的概率更高。交叉操作的目的是产生新的解，是指从遗传空间中以一定的概率选取不同的解，通过基因的交换产生新的解，交叉概率的选取一般是采用自适应的方法。变异操作是保持遗传空间多样性的主要方式，是从遗传空间中任选一个染色体，以某种概率选择染色体基因串上的某一点进行变换。在本文中，选择算子采用随机遍历抽样（sus）；交叉算子采用单点交叉算子，交叉概率为0.7；变异以某个确定的概率随机选择变异的基因，变异概率为0.01；种群大小为40；最大遗传代数为50代。

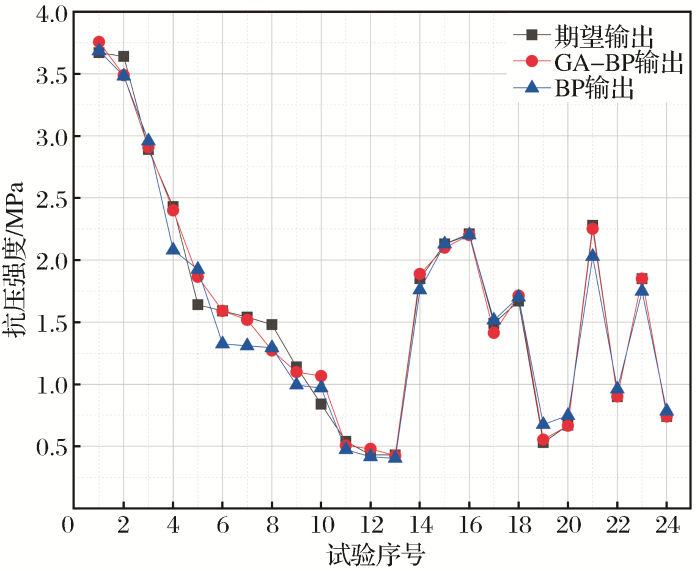
2.2 模型对比分析

将表2中的1~21组数据作为训练集输入到BP神经网络中，并基于遗传算法优化网络权值和阈值以构建GA_BP神经网络，图2展现了训练过程中神经网络期望输出与实际输出之间的误差变化，可以看出在算法迭代50次后，误差收敛到0.017242。随后使用表2中的22~24组数据验证神经网络的预测精度，如图3所示。经验证，GA_BP神经网络的平均相对误差约为0.05%，而未经遗传算法优化的BP神经网络的平均相对误差为6%（表5）。证明构建的GA_BP神经网络，可以大幅提高网络预测的精准度，使其满足所需精度要求。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 GA_BP神经网络训练过程

Fig.2 Training process of GA_BP neural network

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 GA_BP神经网络预测抗压强度效果

Fig.3 Prediction of compressive strength effect by GA_BP neural network

表5 GA_BP 与 BP神经网络的比较

Table 5 Comparison between GA_BP and BP neural network

试验序号	期望输出	GA_BP模型		BP模型
试验序号	期望输出	实际输出	相对误差/%	实际输出	相对误差/%
22	0.90	0.9005	0.05	0.9611	6.79
23	1.85	1.8492	0.08	1.7492	5.45
24	0.74	0.7397	0.04	0.7824	5.73

新窗口打开| 下载CSV

3 遗传算法多目标优化充填料浆配比

基于该矿山技术条件要求^[9]，充填体抗压强度需达1.5 MPa以上。本文在抗压强度满足要求的情况下，优化水泥质量分数（ω₁）、粉煤灰质量分数（ω₂）和尾砂质量分数（ω₃）3种充填料浆配比参数，降低矿山生产成本。其中，水泥单价为340元/t，粉煤灰单价为70元/t，尾砂运价为1元/t，水单价为0.8元/t。

设计参数：Q=[ω₁,ω₂,ω₃]

优化目标：L≥1.5 MPa（抗压强度），P（成本）最小

约束条件：2%<ω₁<16%，0<ω₂<20%，50%<ω₃<75%

3.1 初始种群生成及遗传算子选择

初始种群包括种群规模和种群中个体边界，表6为各配比参数的取值范围，在取值范围内采用二进制编码方式随机产生40个个体作为初始种群，表7为遗传算子参数。

表6 待优化参数及其取值范围

Table 6 Parameters to be optimized and their range of values

配比参数	范围	配比参数	范围
ω₁	2%~16%	ω₃	50%~75%
ω₂	0%~20%

新窗口打开| 下载CSV

表7 全局遗传算子参数

Table 7 Globally optimized genetic operator parameters

遗传算子	取值	遗传算子	取值
最优前端个体系数	0.3	停止代数	200
种群大小	1 000	适应度函数值偏差	1×10^-3
最大进化代数	200

新窗口打开| 下载CSV

3.2 目标函数及适应度函数选择

多目标遗传算法中，有2个目标函数，第一个目标函数是基于各配比组分成本的总金额计算函数，第二个目标函数是基于GA_BP神经网络输出抗压强度的函数，即：

\begin{array}{l} f_{1} (ω_{1}, ω_{2}, ω_{3}) = ω_{1} \times 340 + ω_{2} \times 70 + ω_{3} \times 1 \\ + (1 - ω_{1} - ω_{2} - ω_{3}) \times 0.8 \end{array}

（5）

f_{2} (ω_{1}, ω_{2}, ω_{3}) = s i m (n e t, [ω_{1}; ω_{2}; ω_{3}])

（6）

适应度函数直接影响遗传算法是否收敛，由于MATLAB遗传算法默认求解最小值问题，第一个目标函数是求最小金额，第二个目标函数是求最大抗压强度，因此适应度函数为

\begin{array}{l} f_{1} (ω_{1}, ω_{2}, ω_{3}) = ω_{1} \times 340 + ω_{2} \times 70 + ω_{3} \times 1 \\ + (1 - ω_{1} - ω_{2} - ω_{3}) \times 0.8 \end{array}

（7）

f_{2} (ω_{1}, ω_{2}, ω_{3}) = - s i m (n e t, [ω_{1}; ω_{2}; ω_{3}])

（8）

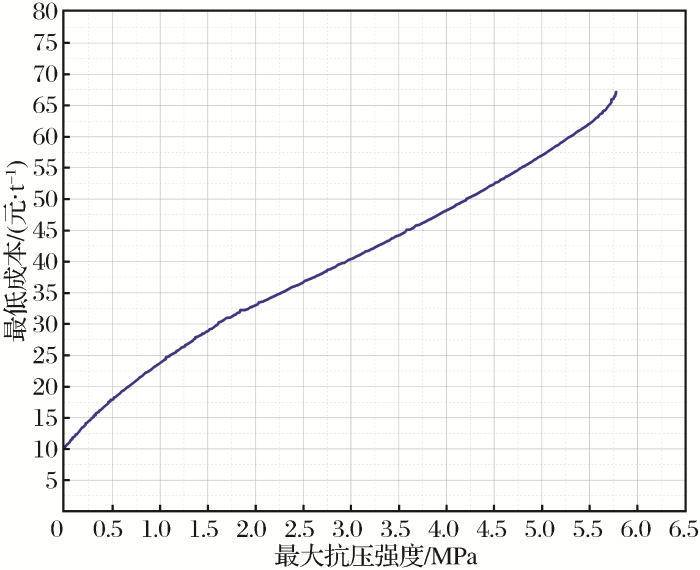
3.3 多目标优化

通过遗传算法多目标全局寻优，迭代200次后得到最优配比组合，如图4所示，算法得到每一个抗压强度下的最低成本及其相应配比组合。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 最优配比组合

Fig.4 Optimum proportion combination

表8展示了抗压强度为1.2~2.0 MPa时的最低成本及其对应配比组合。

表8 不同抗压强度下最低成本及对应的配比参数取值

Table 8 Minimum cost and corresponding ratio parameter value under different compressive strength

参数	不同抗压强度下最低成本时的参数取值
参数	1.2 MPa	1.3 MPa	1.4 MPa	1.5 MPa	1.6 MPa	1.7 MPa	1.8 MPa	1.9 MPa	2.0 MPa
ω₁	7.0	7.4	7.6	8.0	6.8	6.5	8.1	7.2	7.1
ω₂	2.5	2.2	2.9	2.3	9.2	12.0	5.7	10.9	12.5
ω₃	67.2	67.3	67.5	66.8	66.3	66.4	67.8	67.5	69.0
最低成本/（元·t^-1）	26.2	27.4	28.5	29.3	30.4	31.1	32.2	32.7	33.5

新窗口打开| 下载CSV

当水泥质量分数为8%，粉煤灰质量分数为2.3%，尾砂质量分数为66.8%时，每吨充填料成本计算过程为：8%×340+2.3%×70+66.8%×1+（1-8%-2.3%-66.8%）×0.8≈29.3元，与优化结果相符合。根据文献[9]中的试验数据，当水泥质量分数为8.2%，粉煤灰质量分数为0.4%，尾砂质量分数为65.78%时，充填体抗压强度为1.54 MPa，与优化结果基本一致。

4 结论

通过对充填料浆进行多目标寻优，得到以下结论：

（1）通过对样本数据进行分析，建立了3-9-1的BP神经网络，基于遗传算法对BP神经网络初始权值和阈值进行优化，构建GA_BP神经网络，经过测试集数据验证了GA_BP神经网络相比BP神经网络其网络预测精度大幅提高，能够更精确地描述充填料浆配比参数与充填体抗压强度之间的非线性关系。

（2）将已建立的GA_BP神经网络用作目标函数，结合充填料浆总成本的目标函数，通过遗传算法多目标寻优，优化得到每一个充填体抗压强度下的最低成本及对应充填料浆配比参数。优化结果显示，充填体抗压强度为1.5 MPa时的最低成本是29.3元/t，此时的配比组合：水泥质量分数为8%，粉煤灰质量分数为2.3%，尾砂质量分数为66.8%。本文在满足实际生产要求的情况下，采用遗传算法寻找多目标最优解，创新了充填体抗压强度的优化方法，提供了新的思路，在生产实践中具有一定的指导意义。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

于世波, 杨小聪, 董凯程, 等.

空场嗣后充填法充填体对围岩移动控制作用时空规律研究

[J]. 采矿与安全工程学报,2014,31(3): 430-434.

[本文引用: 2]

Shibo

, Yang

Xiaocong

, Dong

Kaicheng

,et al.

Space-time rule of the control action of filling body for the movement of surrounding rock in method of the delayed filling open stoping

[J]. Journal of Mining and Safety Engineering,2014,31（3）: 430-434.

[本文引用: 2]

[2]

由希, 任凤玉, 何荣兴, 等.

阶段空场嗣后充填胶结充填体抗压强度研究

[J]. 采矿与安全工程学报,2017, 34(1): 163-169.